bzoj4671: 异或图——斯特林反演

[BZOJ4671]异或图 - xjr01 - 博客园

 

考虑先算一些限制少的情况

gi表示把n个点的图，划分成i个连通块的方案数

连通块之间不连通很好处理（怎么处理看下边），但是内部必须连通，就很难办了

所以再降低条件，fi表示，把n个点的图，划分成i个"连通块"，保证连通块之间不会有边相连，但是内部可以不连通的方案数

fi计算方法如下：

用Bell(n)的复杂度枚举集合划分，然后相邻集合之间不能连边，

然后考虑凑出符合这个集合划分的图有多少个，异或高斯消元，xi表示第i个图选择与否，如果必须不选，等号右边就是0，否则不管。

求自由元个数

 

fi和gi的关系：

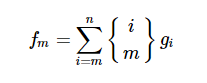
就是枚举到底是有几个连通块

 

然后斯特林反演：

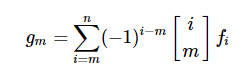
虽然往上枚举，但是式子证明思路是一样的，(-1)项的指数只要保证在所谓[n=m]时候是偶数就好了

 

高斯消元也可以换成线性基

每个图一个元素。每个线性基的位表示这个图这个边有没有，并且再和这次必要的边取&

要求多少个子集xor为全0

线性基之后，2^(s-sz）即可。

 

代码：

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define numb (ch^'0')
#define int long long
using namespace std;
typedef long long ll;
il void rd(int &x){
    char ch;x=0;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*10+numb);
    (fl==true)&&(x=-x);
}
namespace Miracle{
const int M=66;
const int N=66;
int n,m;
int edge[M][12][12];
ll f[12*12];
ll t[N];
int ans[M];
char s[N*N];
ll id[N];
int vis[12*12];
ll Guass(int n){
    memset(ans,-1,sizeof ans);
    memset(vis,0,sizeof vis);
//    for(reg i=1;i<=n;++i){
//        for(reg j=1;j<=m;++j){
//            cout<<f[i][j]<<" ";
//        }cout<<" = "<<f[i][m+1]<<endl;
//    }
//    cout<<endl;
    int free=0;
    for(reg i=1;i<=m;++i){
        int id=0;
        for(reg j=1;j<=n;++j){
            if((!vis[j])&&(f[j]&(1LL*1<<(i-1)))) id=j;
        }
        if(!id){
            ++free;continue;
        }
        vis[i]=1;
        if(id!=i) swap(f[i],f[id]);
        for(reg j=1;j<=n;++j){
            if(j==i) continue;
            if(!vis[j]&&(f[j]&(1LL*1<<(i-1)))){
                f[j]^=f[i];
            }
        }
    }
    return (1LL*1<<free);
}
void dfs(int x,int sz){
    if(x==n+1){
        //cout<<" x "<<x<<" sz "<<sz<<endl;
        memset(f,0,sizeof f);
        int cnt=0;
        for(reg i=1;i<=n;++i){
            for(reg j=i+1;j<=n;++j){
                if(id[i]!=id[j]){
                    ++cnt;
                    for(reg k=1;k<=m;++k){
                        if(edge[k][i][j]) f[cnt]|=(1LL*1<<(k-1));
                    }
                }    
            }
        }
    //    cout<<" cnt "<<cnt<<endl;
        t[sz]+=Guass(max(cnt,m));
        return;    
    }
    for(reg i=1;i<=sz;++i){
        id[x]=i;
        dfs(x+1,sz);
        id[x]=0;
    }
    id[x]=sz+1;
    dfs(x+1,sz+1);
    id[x]=0;
}
void calc(int l){
    for(n=2;n<=10;++n){
        if(n*(n-1)/2==l) break;
    }
}
int main(){
    rd(m);
    for(reg i=1;i<=m;++i){
        scanf("%s",s+1);
        int l=strlen(s+1);
        if(!n) calc(l);
        int t=0;
        for(reg j=1;j<=n;++j){
            for(reg k=j+1;k<=n;++k){
                ++t;
                edge[i][j][k]=edge[i][k][j]=s[t]-'0';
            }
        }
    }
    dfs(1,0);
    ll ans=0,jie=1;
    for(reg i=1;i<=n;++i){
        if(i&1){
        ans+=jie*t[i];
        }else{
        ans-=jie*t[i];
        }
        jie*=i;
    }
    printf("%lld",ans);
    return 0;
}

}
signed main(){
    Miracle::main();
    return 0;
}

/*
Author: *Miracle*
Date: 2019/2/16 21:40:44
*/

 总结：

找到两个数组f，g

f范围宽松好统计，g范围严格难统计但是和答案有直接关系，

这样，只要得到f和g的关系，就可以找到答案！

 

异或下线性方程组的自由元个数：

先变成n*(n+1)的矩阵

然后高斯消元，如果某一个id找不到，那么一定是自由元了，计数器++

注意，每次找i和消除必须在全局位置，并且用一个vis标记表示是否还能动

最后削成的上三角矩阵，除了无解情况，剩下的一定有唯一解