1.14模拟赛

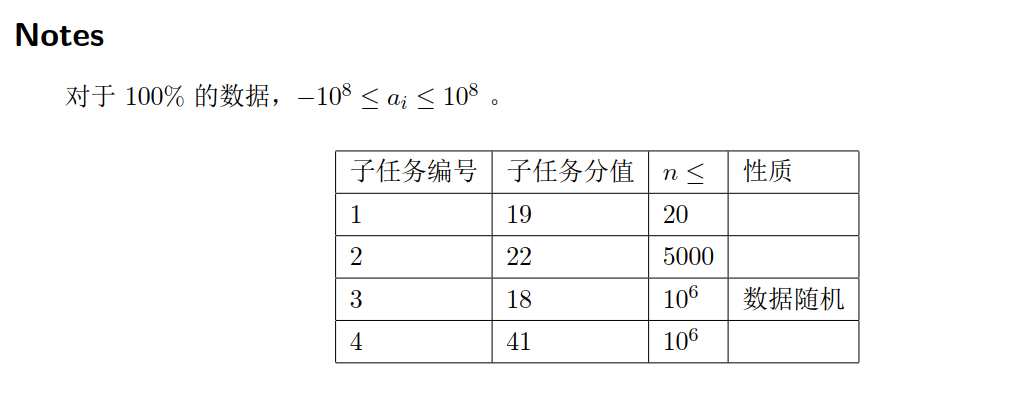
dp式子很好列

展开就是斜率优化。而且横坐标单增，可以直接单调队列

但是权值的偏序比较麻烦

两种方法：

1.权值线段树维护单调队列

权值离散化。线段树每个节点维护所代表的区间的凸包（单调队列）

非常暴力，每次新加入一个点，就在对应位置插入，然后在logn个凸包上插入这个点。由于横坐标单增，所以直接队尾加入即可。

复杂度均摊O(logn）总复杂度O(nlogn)

deque慢死，vector还是慢死，可以开O(nlogn)长度的数组，然后给每个点分配所属的内存。类似于分治的内存分配感觉

 

2.cdq

偏序问题，cdq可以利用下标解决一维

①但是最大的问题是，这个题的dp，按照一般的cdq(l,mid),cdq(mid+1,r)再处理当前，会后效性。正确性不对

②如果cdq(l,mid)处理当前，再cdq(mid+1,r)；本身不能处理好偏序的问题，（不能自底向上归并），暴力sort会TLE。复杂度不对

其实我们第二个方案只要知道当前的排序结果即可。

所以空跑一遍cdq，然后归并，记录每一层最终的排序结果。即可。

（考场上没有想出来先空跑预处理一遍，然后logn层存下来。。。。。。浪费大量时间得到了暴力分的好成绩）

 

T2:

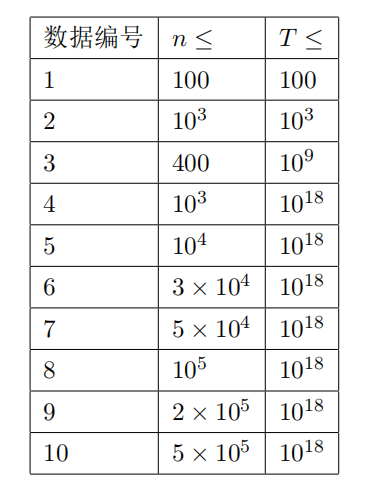
变换可以考虑卷积

xor可以考虑拆位

多项式快速幂

 这个三次变两次：这里有写到：

傅里叶变换(FFT)学习笔记

 

因为其他的项系数都是偶数，直接为0

手玩观察

每一项次数平方，系数也平方。就完成了多项式的平方

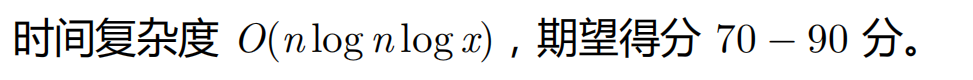
emm。。。其实这一句就够了

但是不从拆位，快速幂，多项式平方的角度推过来，难以想到

暴力模拟：每次跳2^t步，可以找环，然后对于每个i，找所在环的前k个做xor和（前缀和优化）即可。

再加上快速幂的logT

 

T3：

f[i][j]表示，第i个位置放点，包括第i个位置放了j个点，最大收益

考虑区间贡献怎样不算重。

线段树处理每个点的贡献，到了区间左端点，把[1,l-1]加上c；到右端点的时候，把[1,l-1]减掉c

O(nmlogn)

 

 

T1的cdq经验不足啊，，，总是预处理有的时候想不到。。总空间O(nlogn)预处理还是很常见的。。。