[学习笔记]斯特林数
第一类:
S(n,m)表示把n个元素组合成m个圆排列的方案数(注意是圆排列,n个元素的圆排列方案数:n!/n=(n-1)!)

性质:

说几个:
组合
O(n^2)递推式:
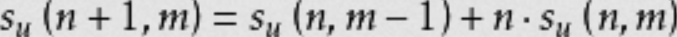
考虑最后一个放在哪里。
代数

第一个式子有一个不错的证明():
考虑递推式,画成横坐标m纵坐标n的图,只能往上或者往右上走,边权不同(1或者i(i是当前纵坐标)),一个路径的价值定义为边权的乘积
求(0,0)到(m,n)的所有路径的价值和。
显然满足O(n^2)递推式
直接考虑,必然m次往右,n-m次往上,所以x(x+1)*...(x+n)中m次幂的系数就是s(n,m)的答案
这就类似于生成函数了
有利于我们寻找nlogn求s(n,*)的式子。
(也可以从Dp(其实就是直接展开)转移式子角度推出系数)
第二个式子,符号和m的奇偶性相关,所以用有符号斯特林数即可
用途:下降幂是因式分解之后的多项式,不利于变换,展开之后,可以方便交换求和号等等
求法

和一般的多项式求逆一样,
f(n)->f(2*n)只要知道f(n+x)的每一项的值
带入后二项式定理展开得到NTT式子。
例题:HDU 4372 Count the Buildings——第一类斯特林数
第二类:
s(n,m)表示把n个不同元素放进m个相同盒子的方案数(m个集合)
性质

求法
还是考虑最后一个放在哪里
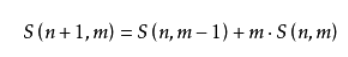
第二类斯特林数(建成二斯)组合意义比较强大(毕竟没有排列苛刻的限制嘛)
通项公式:
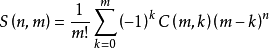
证明考虑容斥,枚举哪些个盒子一定不放球,其他爱放不放(Venn图)
或者反演:


本身通项公式就可以用NTT在O(mlogm)内求出S(n,1~m),
所以出现二斯的时候,可以考虑用通项公式换掉。
组合数可以组合意义处理,n次方,里面还是m-k,考虑能否用NTT优化一下
例题:
[HEOI2016/TJOI2016]求和——第二类斯特林数
组合
上面那个是拆掉斯特林数,
还有一个重要的公式,可以放上斯特林数:
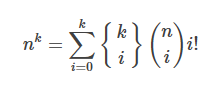

适用于n很大,而k比较小,斯特林数可以快速求出来。
而且,n^k乘方性质通常不够优美,而组合数有丰富的组合意义,并且展开之后的形式也和NTT有些关系
甚至n^k前面还有一些阶乘,可以尝试消一消。
这样n就直接放在了组合数的位置
考虑把组合数拆开消一消,,,把和n有关的枚举都干掉。n放进指数或者底数等可以O(1)或者O(logn)求和的位置
什么时候用通项公式,什么时候把n^k代换呢?
1,考虑n^k和斯特林数哪个好求,或者都试一试
2.根据套路,给了n^k一定换成斯特林数,给了斯特林数换成通项公式。。、。。
比较实际的应用题:


