HDU 4372 Count the Buildings——第一类斯特林数

题目大意：
n幢楼，从左边能看见f幢楼，右边能看见b幢楼

楼高是1~n的排列。

问楼的可能情况

 

把握看到楼的本质！

最高的一定能看见！

计数问题要向组合数学或者dp靠拢。但是这个题询问又很多，难以dp

如果把能看见的和之后挡住的看成一组的话。。。

那么可以看成这样：

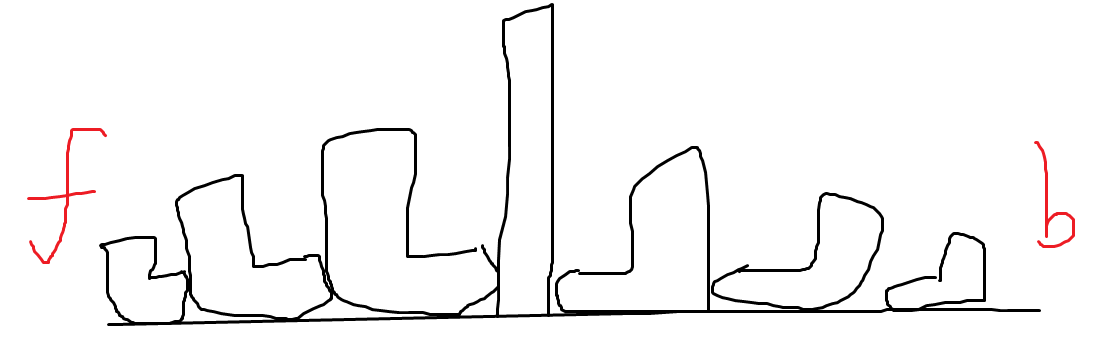
每一组要固定第一个，，后面可以随便动，n!/n=(n-1)!

第一类斯特林数圆排列！

可分成的组数是：S[n-1][f+b-2]（扣除中间最高的）

每一个圆排列只有最大值靠前的唯一展开方式

所以方案数是S[n-1][f+b-2]*C(f+b-2,f-1)（分出这么多组，再选择f-1个放在前面，之后的方案就唯一确定了！）

 

总结：

思路就是考虑分组，然后找到第一类斯特林数的相似点、