12.26模拟赛
T1:

其实非常简单。考试的时候复杂化了。考虑到了各种高级算法。。。。。
区间出现次数考虑前缀差分。考虑什么时候符合要求。
对应字符次数相同意味着左右端点的字符出现的相对次数相同。(即纵向对字符再差分)
所以对纵向差分的值做一个hash即可。
小trick搞定。
注意本题卡哈希。
(我用的分治。复杂度差一些)
T2:


方法众多。
观察复杂度是O(NK)或者O(NKlogN)的
因为有超车情况。。。
一个思路是,考虑d-t图像
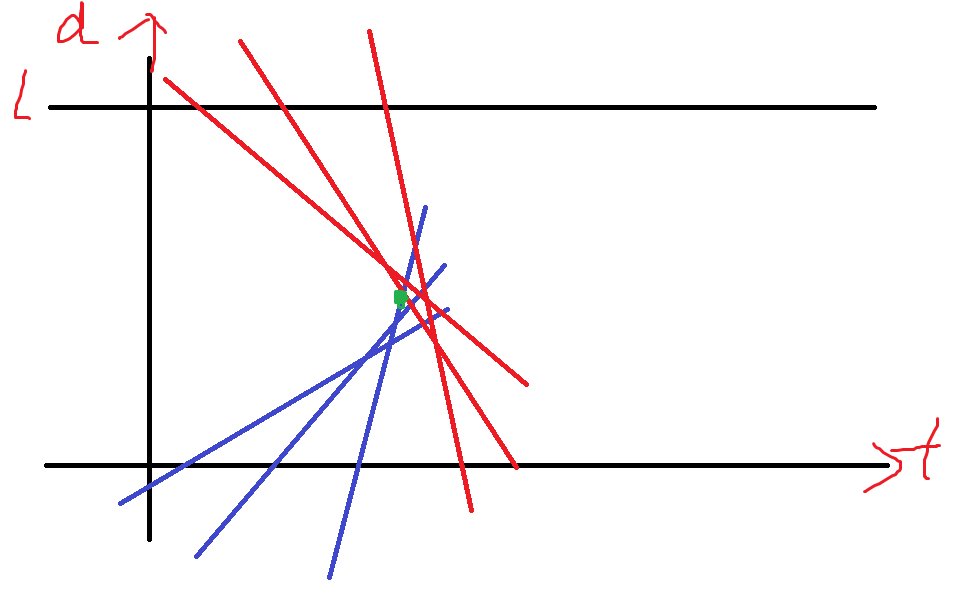
绿色的点是这一次的碰撞点。
怎么找?可以O(NK)所以每次碰撞可以O(N)来找。
该点一定在左凸包上!
然后反过来
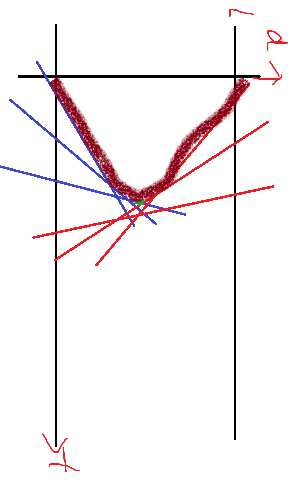
左转:水平可见直线~!
这种特殊的半平面交,按照斜率排序,单调栈即可(一般的半平面交是封闭区间,按级角序排序)
凸包中间属于两侧直线交出的点就是碰撞点(斜率正负交界,易证只有一个)

#include<bits/stdc++.h> #define reg register int #define il inline #define numb (ch^'0') using namespace std; typedef long long ll; il void rd(int &x){ char ch;x=0;bool fl=false; while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb); (fl==true)&&(x=-x); } namespace Miracle{ const int N=100000+5; const int eps=0.0000001; struct po{ double x,y; bool friend operator <(po a,po b){ if(fabs(a.x-b.x)<eps) return a.y>=b.y; return a.x<b.x; } }sta[N]; int top1; struct line{ double k,b; int id; int die; bool friend operator <(line a,line b){ if(fabs(a.k-b.k)<eps) return a.b>b.b; return a.k<b.k; } }l[N],zhan[N]; int pos[N]; int top2; int n,L,K; po calc(line a,line b){//warning!!! pingxing !! po ret; ret.x=((double)b.b-(double)a.b)/((double)a.k-(double)b.k); ret.y=b.k*ret.x+b.b; return ret; } void sol(){ top1=0; top2=0; int i=1; while(l[i].die) ++i; zhan[++top2]=l[i];++i; for(;i<=2*n;++i){ while(i<=2*n&&fabs(l[i].k-l[i-1].k)<eps) ++i; while(i<=2*n&&l[i].die==1) ++i; if(i>2*n) break; while(top1&&calc(l[i],zhan[top2])<sta[top1]){ --top1; --top2; } sta[++top1]=calc(l[i],zhan[top2]); zhan[++top2]=l[i]; } //cout<<" top2 "<<top2<<endl; for(reg i=1;i<top2;++i){ // cout<<zhan[i].id<<endl; if(zhan[i].id<=n&&zhan[i+1].id>n){ printf("%d %d\n",zhan[i].id,zhan[i+1].id-n); l[pos[zhan[i].id]].die=1; l[pos[zhan[i+1].id]].die=1; return; } } return; } int main(){ rd(n);rd(L);rd(K); int v,x; for(reg i=1;i<=n;++i){ rd(x);rd(v); l[i].id=i; l[i].k=-(double)1/(double)v;l[i].b=-(double)x+eps; } for(reg i=n+1;i<=n+n;++i){ rd(x);rd(v); l[i].id=i; l[i].k=(double)1/(double)v;l[i].b=-((double)L/(double)v+(double)x); } sort(l+1,l+n*2+1); for(reg i=1;i<=2*n;++i){ pos[l[i].id]=i; } // for(reg i=1;i<=2*n;++i){ // cout<<i<<" : "<<l[i].k<<" "<<l[i].b<<" "<<l[i].id<<endl; // } for(reg i=1;i<=K;++i){ sol(); } return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* Date: 2018/12/26 15:57:25 */
或者,考虑两个点什么时候会撞上
一定是两边的粒子在某个时刻领先于其他竞争粒子。
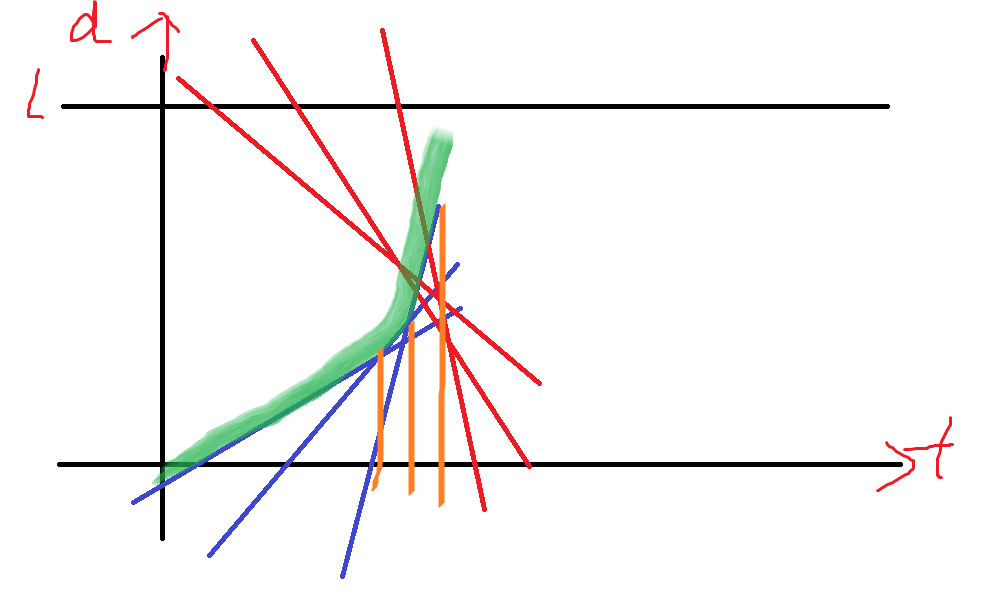
把直线按照横截距排序
橙色的每个区间都可以用单调栈来计算。
两部分直线分别计算
然后形成若干区间

双指针扫描即可。第一个交点就是答案
其实和上面方法本质相同(甚至是新的一种水平可见直线的做法?)
考虑不到图像?
那就尝试考虑过程
两个碰撞上的粒子,是所有剩下粒子中第一个碰撞的。
所以考虑二分碰撞时间T
如果存在一对粒子T时间路程总和>=L那么可以碰撞。
O(NKlog1e9)
卡卡常可过。
进一步考虑两个碰上的粒子满足
L=(T-t1)*v1+(T-t2)*v2
那么,如果二分了一个T
实际上是在找是否存在v1,t1,v2,t2
使得L<=(T-t1)v1+(T-t2)*v2
两部分可以分开找最大值
最大化:f=Tv1-t1v1
t1v1=Tv1-f
斜率优化!
可以对剩余粒子维护分别维护两个凸壳。然后二分
O(NK+Klog^2N+NlogN)
每撞一次,重建一遍凸壳。
T3:


质因子个数很少。又要取模,所以不能爆搜。
就考虑状压DP
记录什么状态?状态要能够支持找到能否加入一个约数
公约数只和质因子有关
6位三进制数记录质因子用了几个。
但是对于6,和2,3显然不同,但是状态就一样了。
如果不能够选择,排除只有一个质因子的情况,那么就是这个约数存在两个不同的质因子,这两个质因子都在之前不同的数中出现过。
所以,暴力一些,记录15位二进制数表示(f1,f2)质数对能否在同一个数中加入进来。
状态转移
枚举用了不到2个的质因子的子集
如果有限制,则不行
否则更新到新的状态。
新的状态处理:三进制质因子部分直接更新。二进制部分,考虑如果某个质因子对,f1之前选择过,f2现在选择了,那么(f1,f2)已经出现在两个不同的数里了,所以不能同时出现。
对于其他情况,一个质数对要么已经变成非法,要么一个没有出现过,要么两个都在这一次出现,所以没有问题
本质上我们通过限制质因子出现与否,以及出现在几个数中,限制了合法条件。
实现的话,状态看似很多,其实很多冗余状态。所以状态不连续。
考虑用map存状态(可以dfs记忆化)
还可以把map存成队列,然后状态从小到大更新,本质上实现了数组的阶段循环或者说花费logn时间实现了一个拓扑排序。(直接一般队列是错的,类比DAG,分层图编号小的不一定拓扑序小啊!)

#include<bits/stdc++.h> #define reg register int #define il inline #define numb (ch^'0') #define mp make_pair #define fi first #define se second using namespace std; typedef long long ll; il void rd(int &x){ char ch;x=0;bool fl=false; while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb); (fl==true)&&(x=-x); } namespace Miracle{ const int N=233; const int mod=1e9+7; ll n; int tot,cnt[N]; map<int,ll>dp; map<int,ll>::iterator r; ll pw[8]={1,3,9,27,81,243,729,2187}; ll ans; int getnew(int st,int chos){ // cout<<" getnew "<<st<<" "<<chos<<endl; int ret=st; int bit=1; for(reg i=0;i<tot;++i){ if((chos&(1<<i))&&st/bit%3<2) ret+=bit; bit*=3; } for(reg i=0;i<tot;++i){ for(reg j=i+1;j<tot;++j){ if((chos&(1<<i))&&(st/bit%2==0)&&(st/pw[j]%3!=0)) ret+=bit; else if((chos&(1<<j)&&(st/bit%2==0)&&(st/pw[i]%3!=0))) ret+=bit; bit<<=1; } } // cout<<" ret "<<ret<<endl; return ret; } ll getsz(int chos){ ll ret=1; // cout<<" chos "<<chos<<endl; for(reg i=0;i<tot;++i){ if(chos&(1<<i)) ret=(ret*cnt[i+1])%mod; } // cout<<" ret "<<ret<<endl; return ret; } void divi(ll x){ for(ll i=2;i*i<=x;++i){ if(x%i==0){ ++tot; while(x%i==0) ++cnt[tot],x/=i; } } if(x>1) cnt[++tot]=1; } int main(){ scanf("%lld",&n); divi(n); dp.insert(mp(0,1)); r=dp.begin(); while(r!=dp.end()){ (ans+=r->se)%=mod; //cout<<r->fi<<" "<<r->se<<endl; int re=0; int bit=1; int now=r->fi; for(reg i=0;i<tot;++i){ if(now/bit%3<2) re|=(1<<i); bit*=3; } int ban[16],top=0; for(reg i=0;i<tot;++i){ for(reg j=i+1;j<tot;++j){ ++top; if((now/bit)&1) ban[top]=(1<<i)|(1<<j); else ban[top]=0; bit<<=1; } } //cout<<" re "<<re<<endl; for(reg to=re;to;to=(to-1)&re){ // cout<<"to "<<to<<endl; bool cont=false; for(reg i=1;i<=top&&!cont;++i){ if(ban[i]&&(ban[i]|to)==to) cont=true; } if(cont) continue; // cout<<" ok "<<to<<endl; int go=getnew(now,to); if(dp.find(go)==dp.end()) dp.insert(mp(go,0)); (dp[go]+=(r->se)*getsz(to))%=mod; } ++r; } ans=(ans-1+mod)%mod; printf("%lld",ans); return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* Date: 2018/12/26 18:58:23 */
总结:
1.T1还是想复杂了。对于题目的度还是把握不好。hash的边走边记录的思想还是不太熟练。对于一个位置多次查询的新旧对比(类似天天爱跑步?)
2.T2一直在想怎么找一个直线和其他直线的前K个交点。。。。还是没有把握好度。由于K比较小。其实O(NK)的复杂度的话,考虑O(N)找到一个,比一股脑塞进去一堆还是要简单自然的。
甚至开始考虑两个点为什么会碰撞也是考虑过的,,,但是二分还是没有想到。还是有些复杂化
3.T3这种不靠谱的状态设计。。。状态数不会太多?还是状压dp比较有把握并且其他题目处理好了再说吧。。。
还是度把握不好。。之后考试应该会有所进步。
最好的方法还是,观察题目的性质,考虑简化的问题,探寻题目条件为什么会成立,为什么会不合法
其次,再是考虑套路(二分,分治,时光倒流,正难则反,容斥),考虑蒙蒙算法
或者手动推推例子找规律



 浙公网安备 33010602011771号
浙公网安备 33010602011771号