于神之怒加强版

https://www.luogu.org/problemnew/show/P4449

k次方。所以不能用$id=\phi * 1$来做。提不出来。

所以只能直接算。那就枚举d=gcd(i,j),d^k再找机会处理。

然后大力反演一波：

 

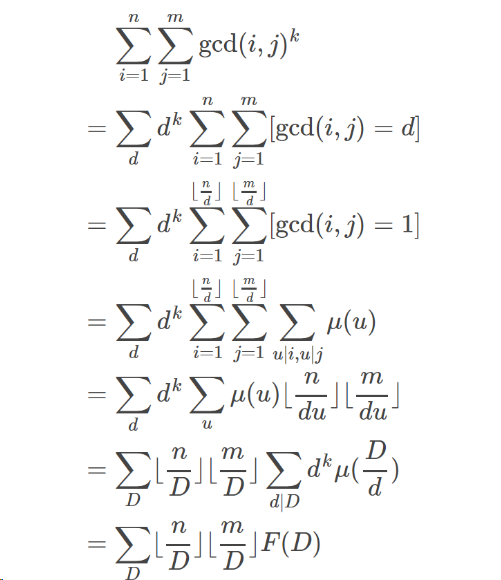
其实很套路。见e就miu，见两项du就D=du（这样的好处是把枚举两个变成枚举一个，另一个的枚举用枚举约数来代替。这样就有可能凑出卷积形式）

后面的F函数是积性函数。直接sieve筛即可。

具体筛法是：

我们考虑p^t能不能单独算。这样在i*pri[j]不互质的时候，可以把i中pri[j]的次数都提出来，然后两边就互质了。

这里，p^t=-p^[(t-1)*k]+p^(tk)

暴力快速幂一下。

记录ci[i]表示i的最小质因子出现次数即可。

（其实可以更好的处理，直接大力分解质因数考虑，把各个质因子独立开来，然后乘上一个数就可以了，节省很多次快速幂）

见：于神之怒加强版

 

注意：

1.sieve别忘了vis[i*pri[j]]=1

2.sieve别忘了if(i%pri[j]==0)....break

3.整除分块，for(i=1,x=0;i<=n;i=x+1)

#include<bits/stdc++.h>
#define il inline
#define reg register int
#define numb (ch^'0')
#define int long long
using namespace std;
typedef long long ll;
il void rd(int &x){
    char ch;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*10+numb);
    (fl==true)&&(x=-x);
}
namespace Miracle{
const int N=5000000+5;
const int mod=1e9+7;
int t,k;
int qm(int x,int y){
    int ret=1;
    while(y){
        if(y&1) ret=((ll)ret*x)%mod;
        x=((ll)x*x)%mod;
        y>>=1;
    }
    return ret;
}
bool vis[N];
int pri[N],ci[N],f[N];
int tot;
void sieve(){
    f[1]=1;
    for(reg i=2;i<=N-3;++i){
        //cout<<" ii "<<i<<endl;
        if(!vis[i]){
            pri[++tot]=i;
            f[i]=(qm(i,k)-1+mod)%mod;
            ci[i]=1;
        }
        for(reg j=1;j<=tot;++j){
            //cout<<" jj "<<j<<endl;
            if((ll)i*pri[j]>N-3) break;
            vis[i*pri[j]]=1;
            if(i%pri[j]==0){
                int lp=qm(pri[j],ci[i]);
                int re=i/lp;
                if(re!=1){
                    f[i*pri[j]]=(ll)f[re]*f[lp*pri[j]]%mod;
                    ci[i*pri[j]]=ci[i]+1;
                }else{
                    f[i*pri[j]]=((ll)qm(pri[j],(ci[i]+1)*k)-qm(pri[j],ci[i]*k)+mod)%mod;
                    ci[i*pri[j]]=ci[i]+1;
                }
                break;
            }
            else{
                f[i*pri[j]]=((ll)f[i]*f[pri[j]])%mod;
                ci[i*pri[j]]=1;
            }
        }
    }
//    for(reg i=1;i<=10;++i){
//        cout<<i<<" : "<<f[i]<<endl;
//    }
    for(reg i=1;i<=N-3;++i){
        f[i]=(f[i]+f[i-1])%mod;
    }
}
int main(){
    rd(t);rd(k);
    sieve();
    int n,m;
    while(t--){
        rd(n);rd(m);
        if(n>m) swap(n,m);
        ll ans=0;
        for(reg i=1,x=0;i<=n;i=x+1){
            x=min(n/(n/i),m/(m/i));
            //cout<<" xx "<<i<<" "<<x<<endl;
            ans=(ans+(ll)(n/i)*(m/i)%mod*((f[x]-f[i-1]+mod)%mod))%mod;
        }
//        for(reg i=1;i<=n;++i){
//            ans=(ans+(n/i)*(m/i)%mod*f[i]%mod)%mod;
//        }
        printf("%lld\n",ans);
    }
    return 0;
}

}
signed main(){
    Miracle::main();
    return 0;
}

/*
   Author: *Miracle*
   Date: 2018/12/13 8:11:06
*/