[HNOI2007]最小矩形覆盖

题目描述

给定一些点的坐标，要求求能够覆盖所有点的最小面积的矩形，输出所求矩形的面积和四个顶点坐标

输入输出格式

输入格式：

第一行为一个整数n（3<=n<=50000），从第2至第n+1行每行有两个浮点数，表示一个顶点的x和y坐标，不用科学计数法

输出格式：

第一行为一个浮点数，表示所求矩形的面积（精确到小数点后5位），接下来4行每行表示一个顶点坐标，要求第一行为y坐标最小的顶点，其后按逆时针输出顶点坐标.如果用相同y坐标，先输出最小x坐标的顶点

 

题解

题目简单易懂。做法扑朔迷离。

首先，矩形的一个边一定和凸包的一条边重合（???貌似无人会证？？？dalao说显然，juruo说是结论？？）。

然后可以旋转卡壳

 

我们需要固定这样几个点：A/B/C/D/E

D是最高点，A,B是枚举的边，C、E是左右最远点。

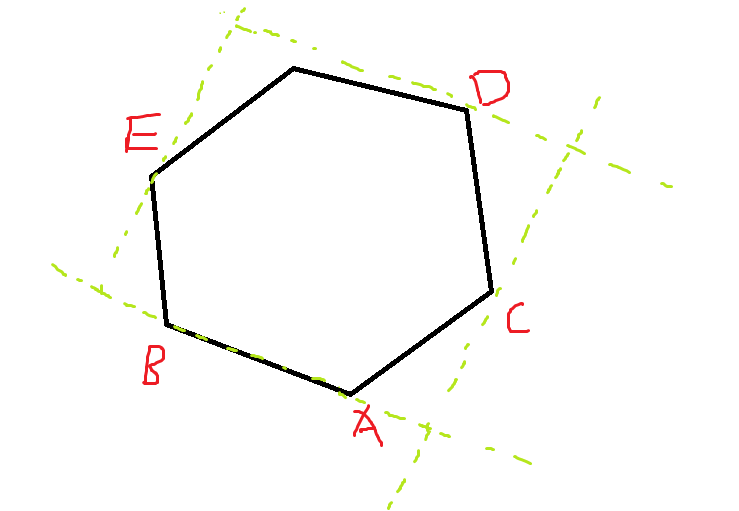
D直接旋转卡壳可以找到。

C，E满足位置转动单调性。

对于C，只要判断，BA向量和AC向量夹角是锐角，

对于E，只要判断，BA向量和BE向量夹角是钝角。

在此基础上，C，E不断移动到不行为止。

锐角钝角可以用点积正负判断。

 

算面积的话，高好说，就是D到AB的距离。

宽的话，是AB+(C在AB上的投影长度)+(E在AB上的投影长度)

投影长度可以用点积计算。

 

然后，矩形四个点怎么算？？

参考ywy大神方法：用相似三角形。

题解 P3187 【[HNOI2007]最小矩形覆盖】

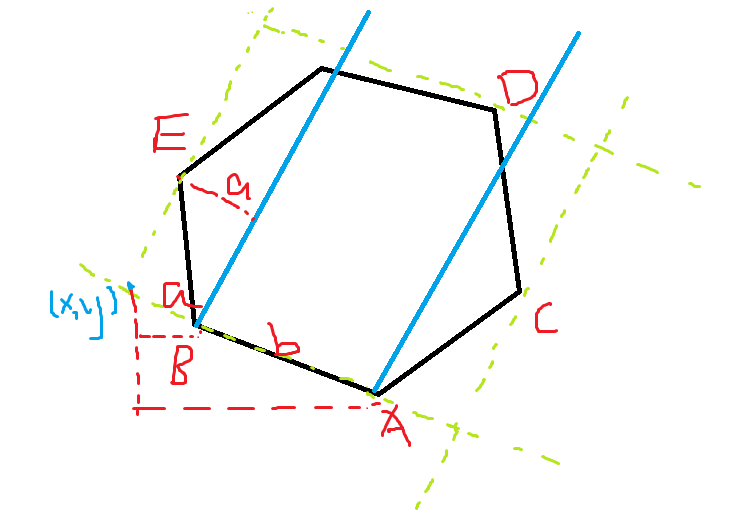
a就是投影。叉积计算即可。

其他三个点同理。

完毕。

 

（PS：这个题貌似就只有一个矩形满足面积最小，，，，我也不知道为什么。。。）

 （但是我还是对每个矩形都求了一下四个点，然后判断的）

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define numb (ch^'0')
using namespace std;
typedef long long ll;
il void rd(int &x){
    char ch;x=0;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*10+numb);
    (fl==true)&&(x=-x);
}
namespace Miracle{
const int N=50000+5;
const double eps=1e-10;
const double inf=1123333333.01;
int n;

struct po{
    double x,y;
    po(){}
    po(double xx,double yy){
        x=xx;y=yy;
    }
    po friend operator +(po a,po b){
        return po(a.x+b.x,a.y+b.y);
    }
    po friend operator -(po a,po b){
        return po(a.x-b.x,a.y-b.y);
    }
    bool friend operator <(po a,po b){
        if(a.y!=b.y) return a.y<b.y;
        return a.x<b.x;
    }
}a[N];
set<po>s;
struct vec{
    double x,y;
    vec(){}
    vec(po a){
        x=a.x,y=a.y;
    }
    double len(){
        return sqrt(x*x+y*y);
    }
};
double dis(po a,po b){
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
double cross(vec a,vec b){
    return a.x*b.y-a.y*b.x;
}
double dot(vec a,vec b){
    return a.x*b.x+a.y*b.y;
}
int Fabs(double t){
    if(fabs(t)<eps) return 0;
    if(t>0) return 1;
    return -1;
}
double hei(po p,po a,po b){
    vec t1=vec(a-b),t2=vec(p-b);
    return fabs(cross(t1,t2))/dis(a,b);
}
bool cmp(po x,po y){
    double t=cross(vec(x-a[1]),vec(y-a[1]));
    if(Fabs(t)) return t>0;
    return vec(x-a[1]).len()<vec(y-a[1]).len();
}
po sta[N];
int top;
double ans;
int mem[10];
po op[10];
po tmp[10];
int m;
int main(){
    scanf("%d",&m);
    ans=inf;
    double x,y;
    for(reg i=1;i<=m;++i){
        scanf("%lf%lf",&x,&y);
        if(s.find(po(x,y))==s.end()){
            //cout<<" new "<<x<<" "<<y<<endl;
            s.insert(po(x,y));
            a[++n]=po(x,y);
        }
    }int id=1;
    for(reg i=2;i<=n;++i){
        if(a[i].x<a[id].x||((a[i].x==a[id].x)&&(a[i].y<a[id].y))) id=i;
    }
    if(id!=1) swap(a[1],a[id]);
    sort(a+2,a+n+1,cmp);
    sta[++top]=a[1];
    for(reg i=2;i<=n;++i){
        while(top>2&&cross(vec(sta[top]-sta[top-1]),vec(a[i]-sta[top]))<0) --top;
        sta[++top]=a[i];
    }
//    cout<<" top "<<top<<endl;
//    for(reg i=1;i<=top;++i){
//        cout<<" ii "<<i<<" : "<<sta[i].x<<" "<<sta[i].y<<endl;
//    }
    int A,B,C,D,E;
    A=1,C=1,B=top,E=top;D=1;
    while(Fabs(dot(vec(sta[E-1]-sta[E]),vec(sta[A]-sta[B])))<=0) --E;
    //n=233333;
    for(reg A=1;A<=top;++A){//i&&i-1
        B=A-1;if(B==0) B=top;
        //if(sta[A]==sta[B]) continue;
        while(Fabs(dot(vec(sta[C%top+1]-sta[C]),vec(sta[A]-sta[B])))>=0) {
            C=C%top+1;
            //cout<<" CCC "<<C<<" : "<<dot(vec(sta[C]-sta[A]),vec(sta[A]-sta[B]))<<endl;
        }
        while(Fabs(dot(vec(sta[E]-sta[E%top+1]),vec(sta[A]-sta[B])))>0) E=E%top+1;
        while(Fabs(fabs(cross(vec(sta[D%top+1]-sta[B]),vec(sta[A]-sta[B])))>fabs(cross(vec(sta[D]-sta[B]),vec(sta[A]-sta[B]))))) D=D%top+1;
        double H=hei(sta[D],sta[A],sta[B]);
        double d=dis(sta[A],sta[B]);
        double L=d+fabs(dot(vec(sta[E]-sta[B]),vec(sta[A]-sta[B]))/d)+fabs(dot(vec(sta[C]-sta[A]),vec(sta[A]-sta[B]))/d);
        //cout<<" A "<<A<<" B "<<B<<" C "<<C<<" D "<<D<<" E "<<E<<" : S "<<H*L<<endl;
        
        double bb=dis(sta[A],sta[B]);
        double aa=fabs(dot(vec(sta[E]-sta[B]),vec(sta[B]-sta[A]))/bb);
        op[1]=po(sta[B].x-aa*(sta[A].x-sta[B].x)/bb,sta[B].y+aa*(sta[B].y-sta[A].y)/bb);
        
        double cc=fabs(dot(vec(sta[C]-sta[A]),vec(sta[A]-sta[B]))/bb);
        op[2]=po(sta[A].x+cc*(sta[A].x-sta[B].x)/bb,sta[A].y-cc*(sta[B].y-sta[A].y)/bb);
        
        H=hei(sta[D],sta[A],sta[B]);
        double tt=dis(op[2],sta[C]);
        op[3]=po(op[2].x+H*(sta[C].x-op[2].x)/tt,op[2].y+H*(sta[C].y-op[2].y)/tt);
        
        double ee=dis(op[1],sta[E]);
        op[4]=po(op[1].x+H*(sta[E].x-op[1].x)/ee,op[1].y+H*(sta[E].y-op[1].y)/ee);
        
        id=1;
        for(reg i=2;i<=4;++i){
            if(op[i].y<op[id].y||((op[i].y==op[id].y)&&(op[i].x<op[id].x))) id=i;
        }
        
        if(Fabs(ans-H*L)>0||(Fabs(ans-H*L)==0&&op[id]<tmp[1])){
            ans=H*L;
            for(reg i=1;i<=4;++i){
                tmp[i]=op[id];
                id=id%4+1;
            }
        }
    }
    printf("%.5lf\n",ans);
    for(reg i=1;i<=4;++i){
        if(Fabs(tmp[i].x)==0) tmp[i].x=0.00;
        if(Fabs(tmp[i].y)==0) tmp[i].y=0.00;
        printf("%.5lf %.5lf\n",tmp[i].x,tmp[i].y);
    }
    return 0;
}

}
int main(){
    Miracle::main();
    return 0;
}

/*
   Author: *Miracle*
   Date: 2018/11/24 18:49:07
*/