【学习笔记】浅谈网络流建模
网络流,网络建模最毒瘤。
本篇学习笔记为本人学习网络流建模的一些基本模型,也作为当前常见网络流建模的一个汇总。
只写了一点,可能有时间再补。
\(last \space updated:2023.3.31\)
有些建模的题只写上来了几道,还会继续更,很多模型还没写上去。qwq
最大流
朴素建模
模板题,按照题目输入连边跑最大流即可。
依照题意输入连边跑最大流即可。
按照题意连 \(a \to b\),容量为 \(c\) 的边,跑一次最大流,记录流量 \(Flow\)。
若 \(Flow = 0\),无解。否则输出答案 \(\left\lfloor \dfrac{x-1}{Flow}\right\rfloor + 1\)。
模板题,源点 \(1\),汇点 \(n\),按照题目输入连边跑最大流即可。
按照题意将 bxy 阵营中每个人向对方阵营中可以击败的人连容量 \(1\) 的边,\(s\) 向 bxy 阵营中每个人连容量为每个人的生命,对方阵营中每个人向 \(t\) 同样连他们生命为容量的边。并且,统计每个阵营中 YYY 的数量,将每个阵营中的 J 的生命加上他所在阵营中的 YYY 数量即可。注意:YYY 给 J 加生命,并不需要浪费 YYY 的生命,所以直接加上即可,不需要连边。
简单拆点题。因为每个石柱只能条 \(h_{i,j}\) 次,所以要将每个点进行拆点。具体来讲,将每个点 \((i,j)\) 拆成 \((i,j),(i,j)'\) 两点,且连边 \((i,j) \to (i,j)'\),容量为 \(h_{i,j}\)。(ps:每个二维点 \((i,j)\) 可以转化为一维的编号 \((i-1) \times m + j\),\(m\) 为最大的第二维度的编号。并且,可以将 \((i,j)'\) 的编号设为 \((i,j) + n \times m\),这样就好处理一点)。再将图中任意两个距离 \(\le d\) 的点 \((x,y)\) 和 \((x',y')\) 连 \((x,y)' \to (x',y')\),容量 \(inf\)。(就是拆点情况下一个点的出点连向另一点的入点) 。源点 \(s\) 向每个蜥蜴点连容量为 \(1\) 的点,每个能直接跳出边缘的点连向汇点 \(t\) 容量 \(inf\)。
三分图匹配
想了想,还是将这个专题放在最大流中,毕竟还是和二分图有点不同之处的。
首先,三分图的定义还是与二分图类似,将所有的点分成三部分,点集 \(A,B,C\)。其中,\(A,B\) 和 \(B,C\) 之间有连边且只有它们间有连边。问这 \(3\) 个点集最大匹配是多少。
传统的匈牙利匹配还是可行的,但极力不推荐。因为三分图的点数更多了,而匈牙利复杂度是 \(O(nm)\) 的,dinic 的复杂度是 \(O(m \sqrt{n})\) 的。
模板的三分图匹配,但因为每个房间和菜只能选 \(1\) 次,所以要对于每个点进行拆点处理,将每个人作为中间点集 \(B\),将每个房间向所有喜欢它的人连边,每个人再向所有他喜欢的菜连边(房间和菜都是要拆点的)。源点 \(s\) 连向所有房间,再将所有菜连向汇点 \(t\)。本题涉及的所有边权都是 \(1\)。(因为都只能选 \(1\) 次呀)
也是和上题类似,三分图匹配的板子。将每本书作为中间点集,答案和练习册作为剩下的两个点集,还是要拆点(只能匹配 \(1\) 个)处理,一样地跑最大流就行。
完全相同的三分图模板,正常跑即可,和上面两题没有什么本质上的区别。注意,还是要拆点的。
分层图
考虑到对于每个飞船的周期行驶和太空站的停留很难处理,所以可以使用分层图来解决这些问题。首先,可以将原图按时间分层,每层都有 \(n\) 个节点表示这个时间点的 \(n\) 个星球情况。当可以表示时间这个维度时,周期也很好处理了。对于每个飞船,将它从上一层停留的节点 连向 按周期行走时到这一层停留的节点。也就是 \(u_{cur-1} \to v_{cur}\)(\(u,v\) 是它运行周期中相邻的两个节点),容量为 \(h_i\)
。同时,因为人可以在每个节点上停留,所以可以对于每个 \(u\) 连 \(u_{cur-1} \to u_{cur}\),容量为 \(inf\)。
连接 \(s \to earth\),容量为 \(k\)。
然后有两种方法:
- 二分
显然可以二分答案,处理这个时间。
每次重新按上面建图,\(s\) 在第一层连接到 \(earth\),容量 \(k\)。在 \(mid\) 层的 \(moon_{mid}\) 连到 \(t\),容量也是 \(k\)。然后跑最大流,如果结果等于 \(k\) 的话,那么就说明这个答案符合要求。
- 累加最大流
可以每层都跑一次最大流,只在上一层跑完的残量网络上跑,不能重新建图。
枚举每个时间,每层从上一层连完后再将每一层的 \(moon_i \to t\),容量 \(inf\)。注意:每一层的月球节点都要向汇点连边,而源点只能在第一层向地球节点连容量 \(k\) 的边。 因为人是可以在地球上停留的,也最多只能给 \(k\) 的流量,不能给多。同理,月球也是可以从上一层继承的,但是不明确最后的节点在哪(因为是枚举时间的),所以每层都要连一遍。
当累加到 \(k\) 时,那么当前的时间 \(cur\) 就是答案。
如何处理无解?
可以使用并查集维护一下连通性(最严谨的),也可以二分时没答案就是无解,或者枚举时间时找个极大值,如果超过它还没解,就是无解。
二分图
最大流跑二分图匹配时,建立超级源点 \(s\) 连接每个左边的节点,将每个右边的节点连到超级汇点 \(t\)。如下图。
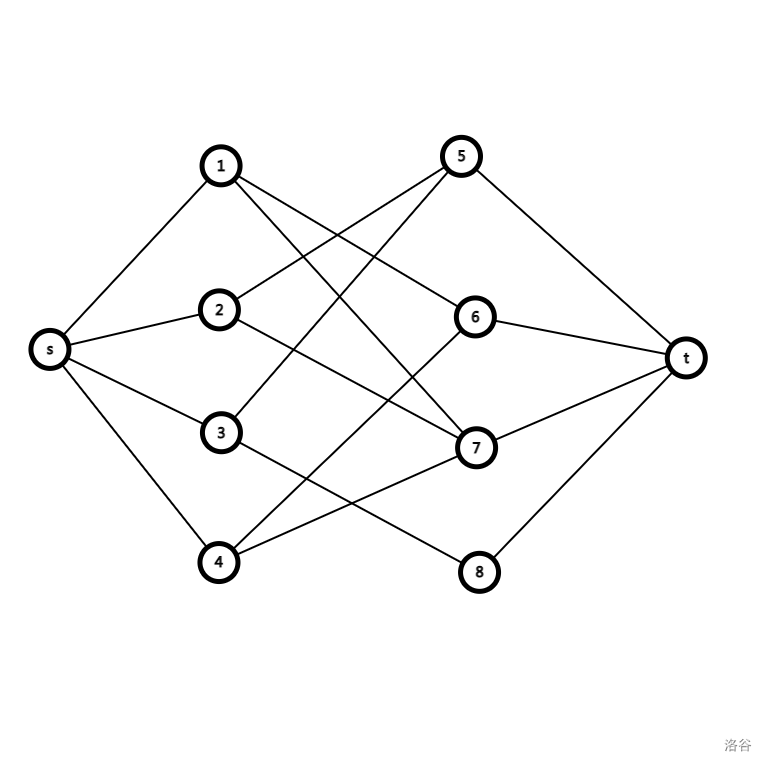
朴素建模
将每个试题 \(i\) 作为左边节点,每种类型 \(p_i\) 作为右边节点。
\(s\) 向每个试题连一条容量 \(1\) 的边,每种类型向 \(t\) 连容量为需求量的边。
每个试题 \(i\) 向每个它可以属于的类型 \(p_{i,j}\) 连容量为 \(1\) 的边。
输出方案时在 残量网络 中寻找 与每个类型连边且不是汇点的 有流量经过 的边,输出那个节点即可。
void print(int u){
for(int i = head[u]; i; i = e[i].nxt){
int v = e[i].v;
if(e[i].w && v <= n){//e[i].w 为正表示残量网络中有流量
//v <= n 是表示边连的是题目的节点而不是汇点。
write(v), putchar(' ');
}
}
}
网格图模型
网格图是天然的二分图,它既可以将所有行和列分成两边的节点,相互连边表示一个点,还可以黑白染色等处理,让其变成一个二分图。
观察题目,手玩一下样例可以发现一个性质:对于任意的行或列,无论进行多少次操作,它的黑点个数都是不变的。
因为对于一个行,和其他行交换明显不会改变它任何状态,交换列也只是将它上面的黑点的位置改变,数量也是不变的。同理,列也是如此。
所以可以考虑把每行当成左边的点,每列当成右边的点,每个黑点 \((x,y)\) 连 \(row(x) \to col(y)\),然后跑最大匹配即可。
如果匹配数为 \(n\) 就是有解,否则无解。
网格图,很快就可以得结论。如果没有 # 的限制就类似八皇后问题。因为每行和每列都只能有一个点,所以可以将行和列组成一个二分图,可以放的地方连边 \(row(x) \to col(y)\),最大匹配。但是有了 # 的限制,如何解决?
可以将每一行和每一列分别分成由 # 隔开的几块,将它们分别编号,如样例:
#***
*#**
**#*
xxx#
将其行列编号:
id:行 id:列
#111 #246
2#33 1#46
44#5 13#6
666# 135#
可以观察到,每一行(或列)当它前面一个字符为 # 时,将其编号加一,也可以理解为每一个 # 往后就是新的一行(或列)。这样就可以解决 # 隔开的问题了。
然后按上述连边跑最大匹配即可。
二分图最小点覆盖(König 定理)
结论:二分图最小点覆盖=最大匹配=最大流
证明:
在证明这个结论前,先来看几条关于二分图匹配的性质:
令左边点集 \(A\),右边点集 \(B\),已匹配的点集为 \(P\),匹配的边集为 \(E\)。
设 \(u \in A,v \in B\),且 \(u,v\) 间有连边
-
若 \(u \notin P\),则必定存在 \(v \in P\)。因为若 \(u,v\) 都没匹配,但它们之间有连边,它们之间必定可以匹配, 所以不可能存在 \(u,v \notin P\) 的情况。
-
若 \(u,u',v,v' \in P; u \to v \in E; u' \to v' \in E\),则肯定不存在 \(u = u',u=v',v=u',v=v'\) 这些情况。因为 \(1\) 个点能且仅能匹配 \(1\) 个点。
-
若 \(u \in P\),则至少存在 \(1\) 个 \(v \in to(u),v\in P\),且必定存在且仅存在 \(1\) 个 \(v\),是直接与 \(u\) 相匹配的。因为若没有任何与 \(u\) 相连且匹配的点,\(u\) 就不可能被匹配。
有了这些性质,就比较好证明了。
- \(P\) 覆盖了所有边
证明:假设存在一条边 \(e \notin E\) 没被覆盖,也就是它的两边的节点 \(u,v\) 均没被匹配(\(u,v \notin P\)),则与性质 \(1\) 矛盾。所以所有边中都至少有 \(1\) 个节点被匹配到。
- $|E| \le $ 最小点覆盖数
证明:由性质 \(3\) 得,\(u\) 至少存在 \(1\) 个与之匹配的 \(v\),则对于边 \(u \to v \in E\), 必定存在 \(u\) 或 \(v\) 来覆盖这个边。又因性质 \(2\),对于每个匹配边 \(u \to v\) 都与其他匹配边 \(u' \to v'\) 不存在交点。则每个匹配边都需要至少 \(1\) 个节点覆盖。所以必定覆盖点数是大于或等于匹配边的数量的。(不然匹配边都没法被覆盖了)
- 构造匹配
从 \(A\) 集的未匹配点 \(u(u \notin P)\) 出发,走未匹配的边。由性质 \(1\) 可得,必定能走到一个 \(v \in P\),再从 \(v\) 走匹配的边到 \(u' \in P\),又从 \(u'\) 走没匹配的边至 \(v'\)。以此类推,最后由匹配边结束(有最大匹配)。那么,可以构造所有 \(u \in A\) 且 \(u\) 没被遍历与所有 \(v \in B\) 且 \(v\) 被遍历过了。这些点数必然是等于 \(|E|\) 的,且根据刚刚的遍历顺序,这些点又必然覆盖了所有边。(可由定理 \(1\) 推导)
因为二分图最小覆盖点数是 \(\ge |E|\) 的(定理 \(2\)),且能构造出一种点数为 \(|E|\) 的点将所有边覆盖。所以,最小覆盖点数肯定是等于 \(|E|\) 的,也就是最大匹配数。
证毕。
二分图最大独立集
在二分图最小点覆盖中,每条边都至少有 \(1\) 个点被选。那么对于所有没有被选的点,不可能在 \(1\) 条边上出现多于 \(1\) 个(因为如果这条边上两个点都没被选,那这条边也不会被覆盖了),所以可以保证没被选的点集是独立的。然而又因为没有更小的点覆盖了,所以最大的独立集也只能是最小点覆盖集的补集(没被选的点),也就是 \(n - |E|\)。
棋盘选点问题
从矩阵上一点出发黑白染色,将它能攻击到的地方染成与它相反的颜色。则可以将原图分为两个点集(黑色与白色的)

如上图,则可以构造一个二分图,将所有黑色的点与所有它能访问到的白色的节点,且能放装置的点连边。然后求最大独立集(要求不能互相攻击)即可。
具体来讲,黑色的点是 \(x + y \equiv 0 \pmod{2}\)的点,白色的点是 \(x +y \equiv 1 \pmod{2}\) 的点。
与 P4304 [TJOI2013]攻击装置 完全相同,按照 P4304 的建图方式跑即可。
与前两题类似,可以先将每个点能攻击到的点黑白染色,可以发现如下规律:

则可以将所有黑色的点连向所有能放置的且能攻击到的白色节点。
黑色的节点是行数为奇数的点,白色的为行数为偶数的点。连边跑二分图最大独立集即可。
最小割
最小割是指将原图划分为两个集合 \(S\) 和 \(T\),其中 \(s \in S, t\in T\),最小的 \(\sum\limits_{u\in S, v \in T} w(u,v)\), \(w(u,v)\) 为 \(u \to v\) 边的边权。
定理:最大流=最小割(仅在数值上相同)
朴素建模
题目描述将图的节点分为两部分,求最小割时,使用朴素建模。
让根节点与所有叶子节点不连通,显然最小割,将所有叶子节点连到汇点 \(t\),源点 \(s\) 为根节点,从根开始往下遍历,在原图的边中,使深度小的点连到深度大的点,最后跑一边最小割即可。
由题意得,\(c1,c2\) 分别是源点和汇点。因为是要求最小的断开电脑数量,所以不能在边上体现,要将每个电脑 \(i\) 拆点为 \(i, i+n\),使 \(i \to i + n\) 边权为 \(1\)。(\(s,t\) 的边权为 \(inf\),因为它们不能被销毁。)然后连双向边 \(u \to v, v \to u\) 都为 \(inf\)(题目中说的是双向联通),跑最小割即可。
题目让我们求将狼和羊分开的最小篱笆个数,也就是最小割。
那么两个格子之间如何连边呢?因为要将羊和狼的格子隔开,所以可以将所有 羊 的节点向周围所有 不是羊 的节点连边权为 \(1\) 的边。又因为有空地的存在,可以在另一方面阻挡羊和狼,所以可以将每个空地周围所有不是羊的节点和它们连边(因为是羊的刚刚连过了)。最后套路将 \(s\) 连向所有羊,所有狼连向 \(t\),边权均为 \(inf\)。最小割就是答案。
题目乍一看,像是一个最小割模板。第一问就直接求最小割即可,关键在于第二问的最少停止的卡车数量。第二问实质上就是求所有的最小割中 最少割掉的 边数量,所以可以考虑将边权都赋为 \(1\) 再求一遍最小割。但是有问题,新的最小割的这些边放到原图中不一定是原图的最小割。所以,只能取第一问最小割中流量流过的边,也就是残量网络中有流量的边,将它们在新图中的边权赋为 \(1\),原图的其他边边权都赋为 \(inf\),这样就能保证以边权最小割为前提下的最少数量了。
网格图
给定一个网格图,让你求最大权值的点集使它们没有公共边。
很显然,当选择一个点后,它所有邻点都不能选了。所以可以对网格图黑白染色,将它的点集分为两个,黑色的和白色的。此时,选择一个黑色的点就不能选它周围的所有白色点,选白色的同理。所以,可以建立一个二分图,左边为黑点,右边为白点,将黑点和所有相邻的白点连边,容量为 \(inf\) (为什么?)。然后 \(s \to black_{i,j}\),容量 \(a_{i,j}\),\(white_{i,j} \to t\),容量 \(a_{i,j}\)。令 \(sum = \sum{a_{i,j}}\),\(sum - mincut\) 就是答案。
简单证明一下。对于一个黑点 \(black_{i,j}\),设它周围的几个点为 \(white_{i-1,j},white_{i,j-1},white_{i,j+1},white_{i+1,j}\)。因为它们之间的连边为 \(inf\),所以不可能成为 \(cut\),所以黑点和它周围的 \(4\) 个白点是必然联通的。
若割掉 \(black_{i,j}\),那么周围的 \(white_{i-1,j},white_{i,j-1},white_{i,j+1},white_{i+1,j}\) 就不会与 \(s\) 联通,剩下的贡献是这 \(4\) 个白点。
若割掉 \(white_{i-1,j},white_{i,j-1},white_{i,j+1},white_{i+1,j}\),那么剩下的贡献就是 \(black_{i,j}\) 的权值,也不会与 \(t\) 联通了。
对于所有这样的一组点,割断的方式必定是两种中的一种,所以肯定能使它们在原网格图中不连通。
又因为最小割是上述两种割掉的权值中的最小值,所以用所有节点的权值和减去它,剩下的必定是最大的。
分组问题(二选一问题,相同分组计算贡献)
分组问题、二选一问题,便是要将每个物品分到两个集合 \(A,B\) 中,分到集合 \(A\) 的花费(或收入)是 \(a_i\),放到集合 \(B\) 的花费(或收入)为 \(b_i\)。
对于建模,可以将每个物品 \(i\),连 \(s \to i\),表示分到 \(A\) 集合,边权为 \(a_i\)。连 \(i \to t\),表示分到 \(B\) 集合,边权为 \(b_i\)。此时最小割就是分组的最小花费了(同理,所有边权之和 \(sum\) 减去最小割就是最大收入 \(sum - mincut\)),因为每个节点都连到 \(s\) 或 \(t\),要想让它们不连通,只能断掉到 $s $ 或到 \(t\) 的边了,也就是选——最小花费(或不选——最大贡献)哪一条边。
关于这类问题,往往会有一些附加条件。最常见的便是对于几个物品 \(p_1,p_2 \dots p_m\),全都在相同的分组(集合)中会有额外的贡献,求最大的总贡献。例如这 \(m\) 个物品都在 \(A\) 集合时的贡献为 \(c_1\),都在 \(B\) 集合时有贡献 \(c_2\)。考虑在连边中表现出这个贡献。如果都在集合 \(A\),便可以设立虚点 \(x\),使得 \(s \to x\),容量为 \(c_1\), \(x \to p_1,p_2 \dots p_m\) 连 \(m\) 条边,容量都是 \(inf\)。此时最小割就是答案,为什么?
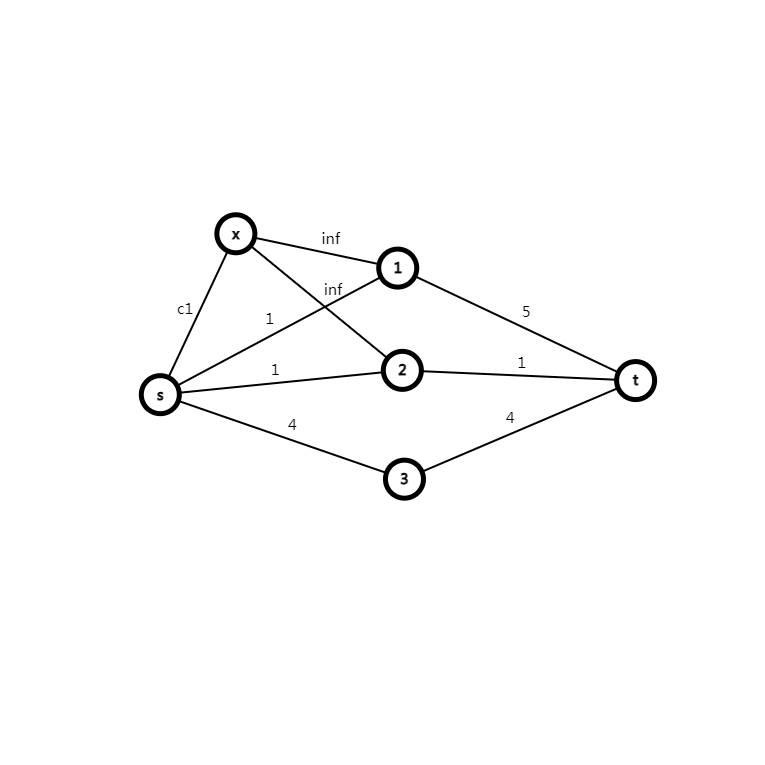
考虑上图,若 \(1\) 在集合 \(A\), \(2\) 在集合 \(B\),那么会怎样?(不考虑 \(3\) 节点)
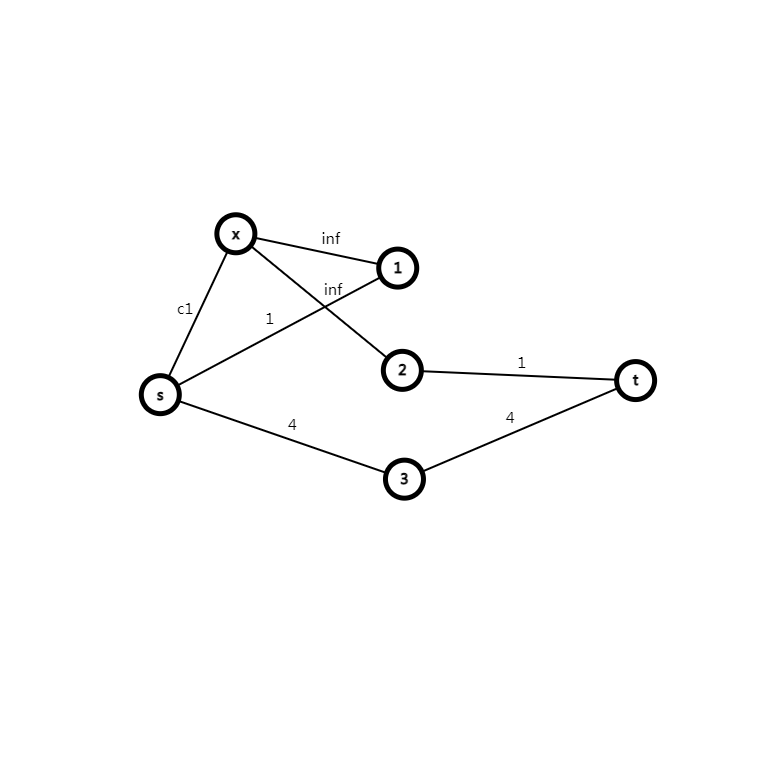
那么,在这种情况下, \(s\) 到 \(t\) 还是联通的,因为有这个虚点 \(x\) 的存在。
又因为 \(x \to 2\) 边权为 \(inf\),所以 \(c1\) 这个贡献肯定是被割掉了。
同理,当 \(1,2\) 没有同时属于集合 \(A\) 时,\(c1\) 都会被割掉。
所以,只有在 \(1,2\) 共同属于 \(A\) 时,\(c1\) 才不会被割掉,会加到 \(sum\) 中不会被减去。(因为收入= \(sum - mincut\))
那么,同理,\(c_2\) 也是类似的连边。
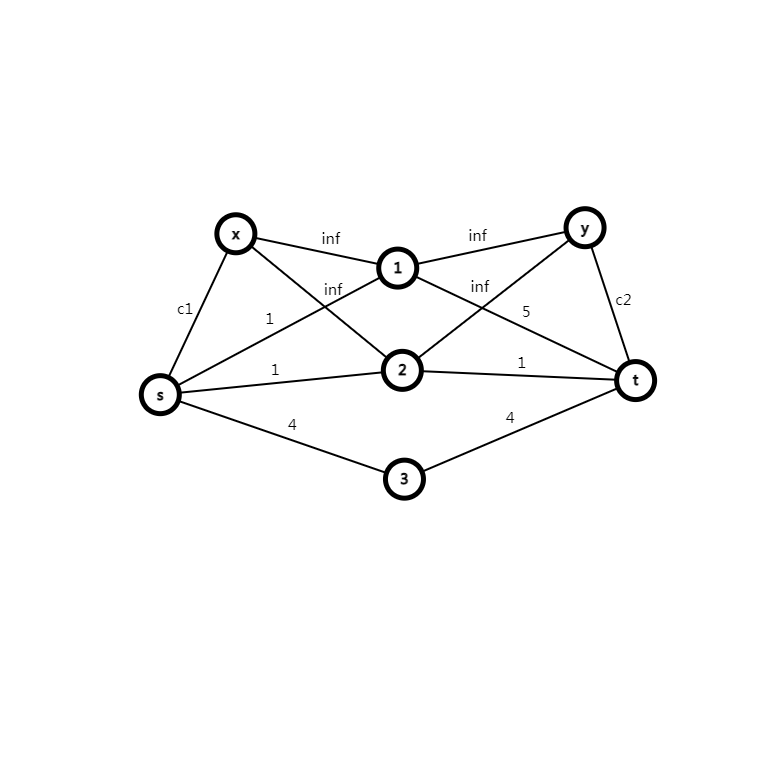
模板题,直接套用刚刚的模型 \(s \to i\) 表示 \(i\) 在 \(A\) 种植, \(i \to t\) 表示在 \(B\) 种植,对于每种组合按上述方法建立虚点,跑最小割即可。
答案就是 \(sum - mincut\)(最大收益)。
类似的二选一问题,但是将贡献从 \(p_1,p_2\) 在相同集合中会有收益变为了它们不在同一集合时有花费,如何解决?
假如说没有好朋友的限制,就直接将每个小朋友依照意愿向 \(s\) 或 \(t\) 连边即可。
有了好朋友的限制,可以将每对好朋友 \(u,v\) 连 \(u \to v\),\(v \to u\) 的边,表示它们在相同立场(双向边是因为朋友关系是对称的,a 是 b 的朋友,b 也是 a 的朋友),最小割就是答案。
证明:若割掉了朋友之间的连边,相当于多一个朋友之间冲突的花费,对于他们的本身意愿没有影响。若割掉两人其中一个向源或汇点连的边,相当于舍弃自身意愿,满足好朋友,就是与本身意愿冲突的花费。
模板,套用上述模型。每个点连到文科(\(s\))和理科(\(t\)),再相邻每两个人之间建立两个虚点表示同选文科或理科即可。
同上题,只是将相邻两个人分组相同的贡献改成周围的人都与其相同的贡献,套模型即可。
也是一道经典的分组问题。但这题的变化之处在于不同分组有贡献。
但是,不同分组的正贡献是无法用这个模型来表示出来的,所以要考虑转换思路,如何将不同分组转换为相同分组。
可以将原网格图进行黑白染色,任意相邻两格黑白颜色均不同,那显然可以将原图分为两种节点(注意:这里不是二分图,只是点类型不同)黑或白。将黑色或白色节点的权值倒置(将原来分到 \(A\) 集合的权值 \(a_i\) 分到集合 \(B\),原来分到 \(B\) 集合的 \(b_i\) 分到集合 \(A\)),这样做并不会对每个点自身的取值有任何影响,因为选两集合中的一个都是对称的,没有本质上的不同。而且,这样做完美地将不同集合转化成了同一集合(因为将其中一种颜色的所有点权值倒置了),就能直接套用模型了。
具体来讲,将 \((x + y) \equiv 1 \pmod 2\) 的节点的 \(a_i\) 与 \(b_i\) 交换。然后相邻两节点同上建立两个虚点,分别向 \(s\) 和 \(t\) 都连 \(c_{i,j} + c_{newi,newj}\)(因为选集合就行了,不论都选哪个集合都是等价的)。然后用所有权值和减去最小割即可。
一道好题,主要难点就是求不同分组的负贡献。如果先不考虑两个节点不同集合带来的负贡献的话,那么就是分组问题的模板。对于两个相同集合的点,建立虚点 \(x'\),使得 \(s \to x'\) 边权 \(EA\),然后 \(x' \to u\),\(x' \to v\) 边权 \(inf\),连到 \(t\) 同理。然后考虑将这个负贡献加进来,因为不能直接表现,所以要将其转化为相同分组的贡献。因为最后的答案是 \(sum - mincut\),所以可以想到在这个最小割中将贡献转为正,然后在权值和中不加上它,最后的贡献就是负的了(相当于 \(sum - (mincut + EC)=sum - mincut - EC\))。有了这个思路,那么接下来的就很好理解了。将 \(s \to x'\),\(y' \to t\) 中的边权都加上 \(EC\),然后在 \(sum\) 中加上一个 \(EC\)。此时,若这两个节点在同一集合,那么 \(mincut\) 中会有一个 \(EC\),\(sum\) 中多加的一个 \(EC\) 和它正好抵消了。若它们不在同一集合,那么 \(mincut\) 中会有两个 \(EC\),此时的贡献正好多了个 \(-EC\),巧妙地将它的负贡献表示出来了。
具体实现可以见 link。
最大权闭合子图
最大权闭合子图,指在一张有向图 \(G\) 中选择一张子图 \(G'\),使得 \(\forall u \in G', to(v) \in G'\),\(to(u)\) 指 \(u\) 在原图中的后继,求最大 \(G'\) 权值和。文字化来讲,就是选出一些节点,让它们的后继都被选,也就是选了一个节点 \(u\) 就必须选所有他的后继 \(v \in to(u)\),你要让这些选出来节点的和最大(每个节点的权值可以为负数)。
对于建模,因为不能有负容量的边,所以只能另想办法。
设每个点的点权为 \(a_1,a_2 \dots a_n\)。
若 \(a_i > 0\),则 \(s \to i\),权值为 \(a_i\)。
若 \(a_i \le 0\),则 \(i \to t\),权值为 \(-a_i\)。
然后将原图中所有 \(u \to v\) 的边权设为 \(inf\)。
所有正权值之和 \(sum\) 减去最小割 \(mincut\) 即是答案。为什么?
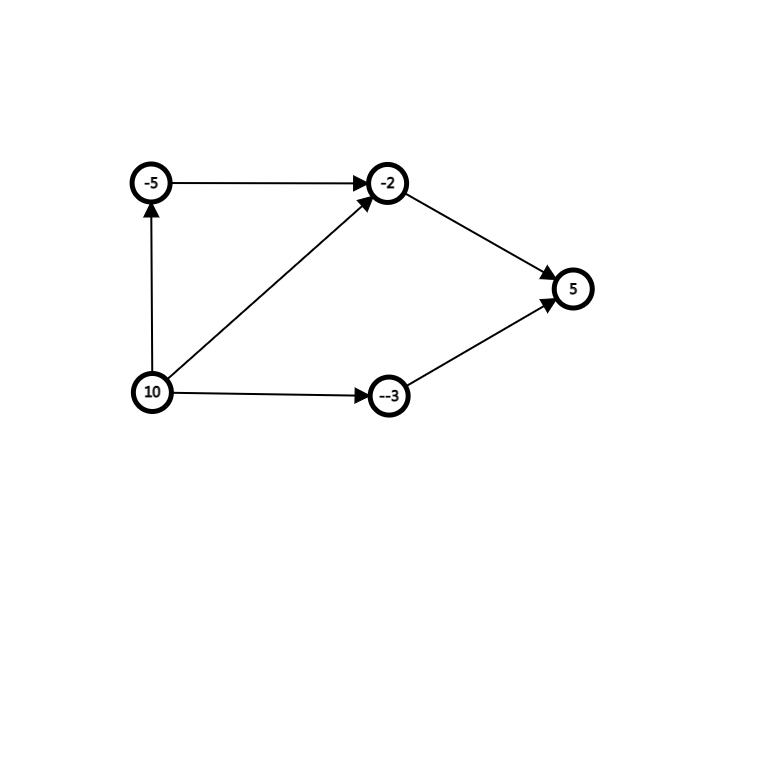
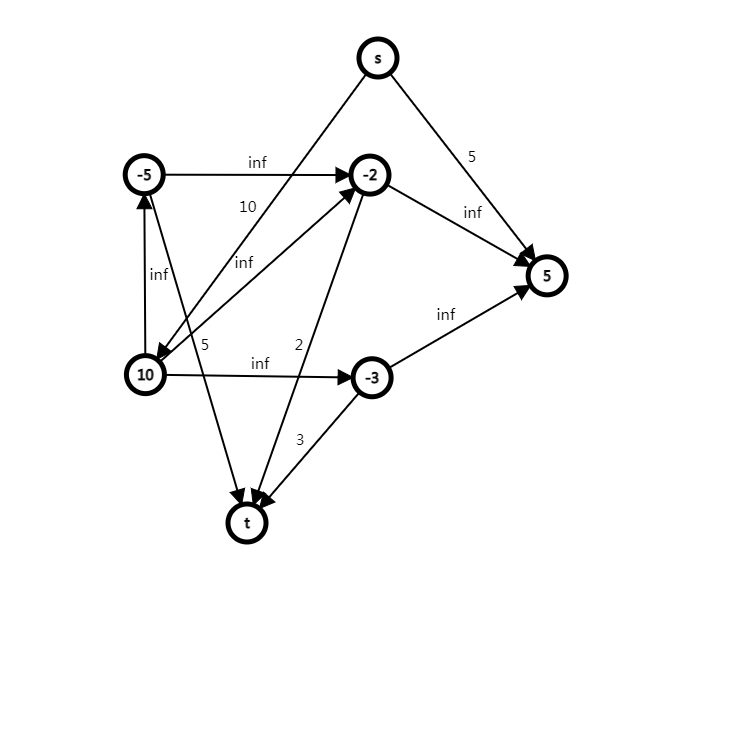
此时,因为原图中的每条边边权都为 \(inf\),所以最小割不可能割到它,后继全取到的条件满足了。
再考虑断边的情况。
若不取一个正权值点,例如上图的 \(s \to 10\) 的边断开后就不会通过这个点联通,那么 \(sum\) 中原本的 \(10\) 也会被减去,所以不会影响。
若取了一个正权值点,例如上图的 \(s \to 10\) 的边联通,那么这时 \(s\) 到 \(t\) 还是联通的,要考虑继续割边。又因为原图中所有的边都不会被断开,所以能断开的就是这个点能走到的所有负权值点与 \(t\) 的边,在上图的例子中就会割掉 \(-5 \to t,-3 \to t, -2 \to t\) 三条边,如下图。
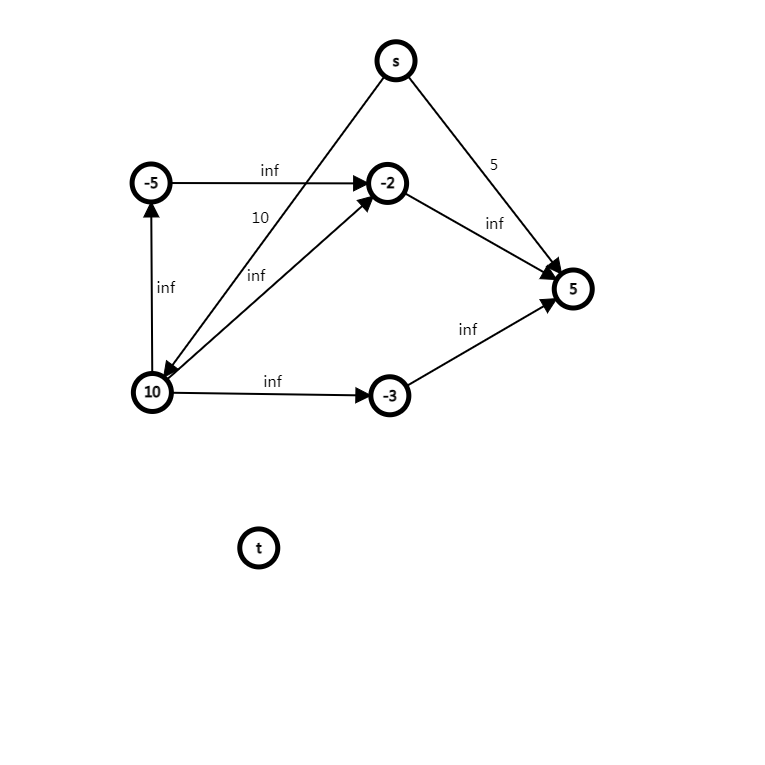
这时,断掉的边 \(mincut = 5+2+3\) 正好对应 \(-5,-2,-3\) 权值和的相反数。那么用 \(sum - mincut\),那么它的贡献正好又变成负的了,完美地解决了正负性的问题。
所以,选出来和的最大值就是 \(sum - mincut\)(使割掉的正权值 和割掉的负权值和的相反数 最小)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号