【学习笔记】浅谈后缀数组SA
后缀数组
算法介绍
后缀数组(suffix array, 简称 SA),是一种强有力的字符串处理算法
能在优良的时间复杂度下解决大部分字符串问题
其核心思想就如它的名字——将字符串每个后缀按字典序排序,并记录下它的编号和排名
算法定义
在本篇文章中,字符串的下标一律从 \(1\) 开始,长度为 \(n\),即 \(s[1...n]\)
后缀数组主要涉及到 \(2\) 个数组:
\(sa[i]\) : 表示 排名为 \(i\) 的后缀 的编号
\(rk[i]\) : 表示 后缀 \(i\) 的排名
其中,后缀 \(i\) 表示从下标 \(i\) 开始到字符串末尾的后缀字符串
\(s[i...n]\)
性质:$\forall 1 \le i \le n, sa[rk[i]] = rk[sa[i]] = i $
显然,这条性质是正确的
排名为【后缀 \(i\) 的排名】的后缀是 \(i\)
【排名为 \(i\) 的后缀】的排名是 \(i\)
图例:
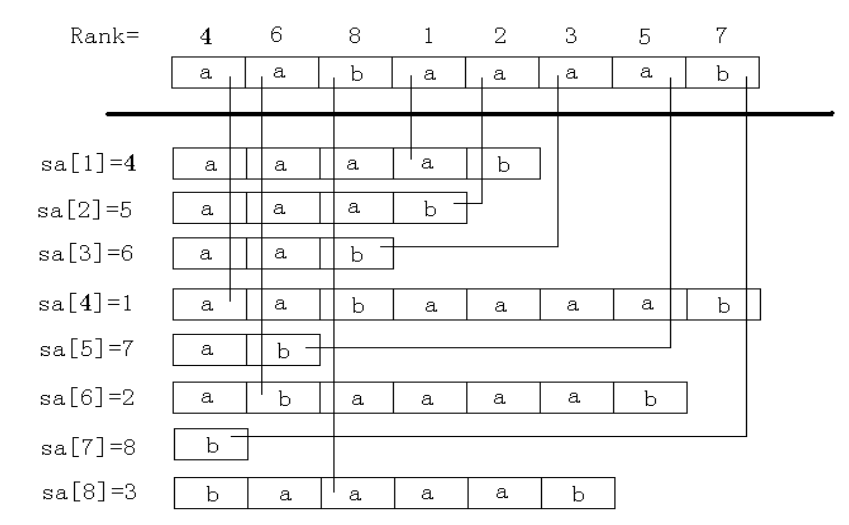
算法详解
暴力 \(O(n^2\log n)\)
最暴力的做法
对于每个后缀 \(i\),截取它存下来
再 \(sort\) 排序
空间复杂度 \(O(n^2)\)
排序 \(O(n \log n)\),比较 \(O(n)\)
时间复杂度 \(O(n^2\log n)\)
暴力做法时空都会爆炸
倍增 \(O(n\log^2n)\)
对于这种每个字串长度较大的问题,不妨试试使用倍增的思想
依次处理从 \(i\) 开始长度为 \(2^k\) 的子串 (\(0 \le k \le \log_2{n}\))
就可以处理出 \(rk[i][k]\) 与 \(sa[i][k]\)
-
对于长度为 \(1\) 的序列直接 \(O(n\log n)\) 暴力排序即可
-
对于长度为 \(2 ^ k\)(\(k > 0\)) 的序列可以从 $ k - 1$ 的部分转移过来
那如何转移呢? 回忆一下字典序比较
对于两个字符串 \(s1\) 和 \(s2\),从头开始枚举 \(i\)
若 \(s1[i] < s2[i]\) 则立刻返回 \(s1 < s2\),不用继续比较,反之同理
若 \(s1[i] = s2[i] (\forall i)\),那么这两个字符串的字典序相同
因为对于当前问题所有子串长度都为 \(2^{k-1}\),所以就不考虑长度不同的了
回到本问题,现在已经知道了所有 \(rk[i][k-1]\)
那么显然对于 \(rk[i][k]\) 可以通过 \(rk[i][k-1]\) 和 \(rk[i + 2^{k-1}][k-1]\) 转移
所以,可以将 \(rk[i][k-1]\) 和 \(rk[i+2^{k-1}][k-1]\) 作为第一、二关键字排序,便可以得到所有 \(s[i...min(i+2^k-1,n)]\) 的排名。如果 \(i + 2 ^ k - 1 > n\),也就是说这个子串不是完整的,那么将它的第二关键字设为无限小(最小),第一关键字和前面相同,延续上一次排序后的 \(rk[i][k-1]\)。然后,在sort一下即可
空间优化:因为每次只需 \(k-1\),所以使用滚动数组,或用另一数组记录上一次求出的 \(rk\) 即可;而每次的 \(sa\) 都不会被用到,所以不用开第二维
复杂度倍增 \(O(\log n)\),排序 \(O(n\log n)\)
所以复杂度为 \(O(n\log^2n)\)
代码就不放了,实现很简单,也不是主流做法。
对于 \(n \ge 500000\) 时,就会爆炸了,所以还需要优化
图例:
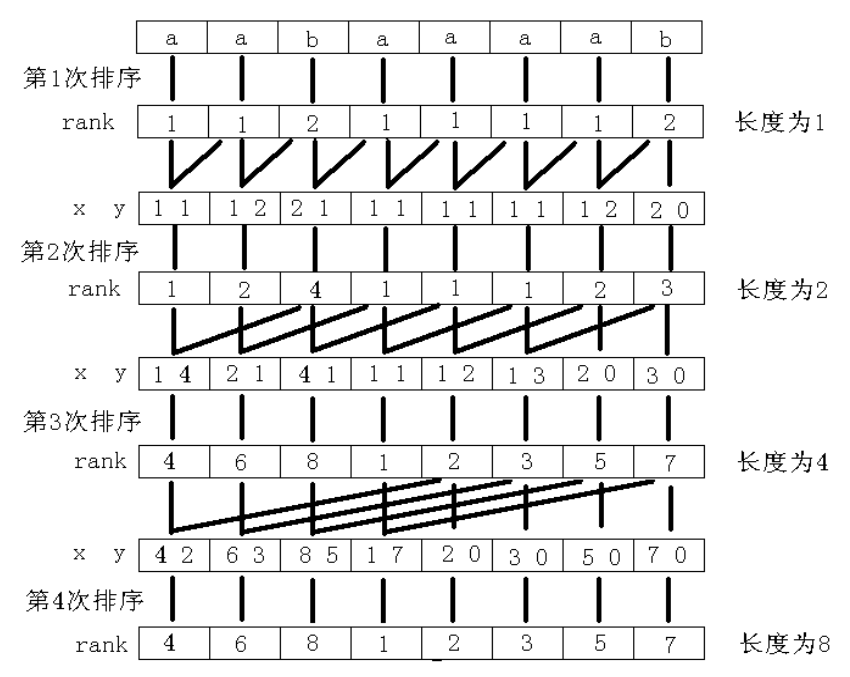
倍增+基数排序 \(O(n\log n)\)
因为所有排名的值域不会超过 \(n\),所以就可以使用基数排序代替sort达到复杂度少一个 \(\log\)。
基数排序是一种稳定的 O(值域) 的排序方法,通常在值域较小时使用
-
对于单关键字:直接用一个桶 \(c\) 记录各值域的出现次数,将它做一个前缀和,这时 \(c[i]\) 就是值域 \(i\) 的排名了。但注意,每次查完值域 \(i\) 的排名就要将它 - 1,因为相同值域可能有多个值。
-
对于多关键字,因为排序的优先级是从低关键字到高关键字的,要使当前关键字排序后不对后续产生影响,所以从高关键字到低关键字依次排序。如果从第一关键字开始排序的话,那最终的结果是按最后一个关键字优先的,所以只能采取依次从第 \(k,k-1,k-2...1\) 关键字排序。
对于此算法,只需用双关键字,所以先将第二关键字基数排序,再排第一关键字即可。
举个例子:
将 \((1,1),(1,2),(2,1),(1,3),(2,2),(2,1)\) 从小到大排序
首先按第二关键字排序
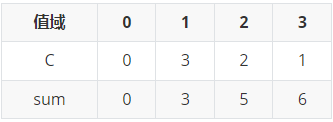
所以,排名如下

排序结果:\((1,1),(2,1),(2,1),(1,2),(2,2),(1,3)\)
再按第一关键字排序
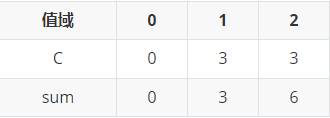
所以,最终的排名为(按第一次排序后的编号)
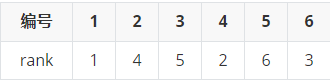
排序结果:\((1,1),(1,2),(1,3),(2,1),(2,1),(2,2)\)
常数优化
- 其实第二关键字不需要基数排序
-
对于长度超范围的,直接将其列入排序结果的首部(因为第二关键字为最小值)
-
对于在范围内的,按上一次更新完的 \(sa\) 依次从下标 \(1\) 到 \(n\) 遍历,存在 \(sa[i] - 2^k > 0\) 的,将 \(sa[i] - 2 ^ k\) 放入排序结果(也就是当前的 \(sa[i]\) 为 以 \(sa[i]-2^k\) 为第一关键字排序的 第二关键字)。根据 \(sa\) 的定义,按顺序遍历 \(sa\) 取出的结果就是已经从小到大排过序的(\(sa[i]\) 为第\(i\) 名的编号),所以可以证明它的正确性。
这样的做法是严格 \(O(n)\) 的,比一次基数排序的常数小一点
- 对于不同的排名等于 \(n\) 时,可直接结束
不断倍增下去时实际上是使这个排名越来越精准,不出现重复。
但如果当前已经是不重复的了,就没必要继续倍增下去。
代码
这是 P3809 模板题的代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
namespace fastio{
template<typename T> inline void read(T &t){
int x = 0, f = 1;
char c = getchar();
while(!isdigit(c)){
if(c == '-') f = -f;
c = getchar();
}
while(isdigit(c)) x = x * 10 + c - '0', c = getchar();
t = x * f;
}
template<typename T, typename ... Args> inline void read(T &t, Args&... args){
read(t);
read(args...);
}
template<typename T> void write(T t){
if(t < 0) putchar('-'), t = -t;
if(t >= 10) write(t / 10);
putchar(t % 10 + '0');
}
};
using namespace fastio;
const int N = 1e6 + 5;
char s[N];
int n, m = 130, x[N], y[N], c[N];//x即rk
int sa[N];
void SA(){
for(int i = 1; i <= n; ++i) c[x[i] = s[i]]++;
for(int i = 1; i <= m; ++i) c[i] += c[i-1];
for(int i = n; i >= 1; --i) sa[c[x[i]]--] = i;
//对长度为1的基数排序
for(int k = 1; k <= n; k <<= 1){
int p = 0;
for(int i = n - k + 1; i <= n; ++i) y[++p] = i;
for(int i = 1; i <= n; ++i){
if(sa[i] > k){
y[++p] = sa[i] - k;
}
}
//第二关键字无需基数排序
for(int i = 1; i <= m; ++i) c[i] = 0;
for(int i = 1; i <= n; ++i) c[x[y[i]]]++;
for(int i = 1; i <= m; ++i) c[i] += c[i-1];
for(int i = n; i >= 1; --i) sa[c[x[y[i]]]--] = y[i];
//对第一关键字基数排序
y[sa[1]] = 1, p = 1;
//将x设为旧的rk,y为新的rk,最后再调换回来,节省空间
for(int i = 2; i <= n; ++i){
y[sa[i]] = (x[sa[i]] == x[sa[i-1]] && x[sa[i] + k] == x[sa[i-1] + k] ? p : ++p);
}
swap(x, y);
if(p >= n) break;
//如果排名都不相同,就可以不用继续了
m = n;
}
}
signed main(){
scanf("%s", s + 1);
n = strlen(s + 1);
SA();
for(int i = 1; i <= n; ++i) cout << sa[i] << ' ';
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号