将真分数分解为埃及分数
自然语言解决问题:
真分数 (a proper fraction): 分子比分母小的分数,叫做真分数。真分数的分数值小于1。如 1/2,3/5,8/9等。
分子是 1的分数,叫单位分数。古代埃及人在进行分数运算时,只使用分子是 1的分数。因此这种分数也叫做埃及分数,或者叫单分子分数。
如8/11=1/2+1/5+1/55+1/110。我们约定分子分母都是自然数,分数的分子用 a 表示,分母用b表示。若真分数的分子 a 能整除分母 b,则真分数经过化简就可以得到埃及分数:若真分数的分子不能整除分母,则可以从原来的分数中分解出一个分母为 (b/a) +1 的埃及分数。用这种方法将剩余部分反复分解,最后可得到结果。
流程图:
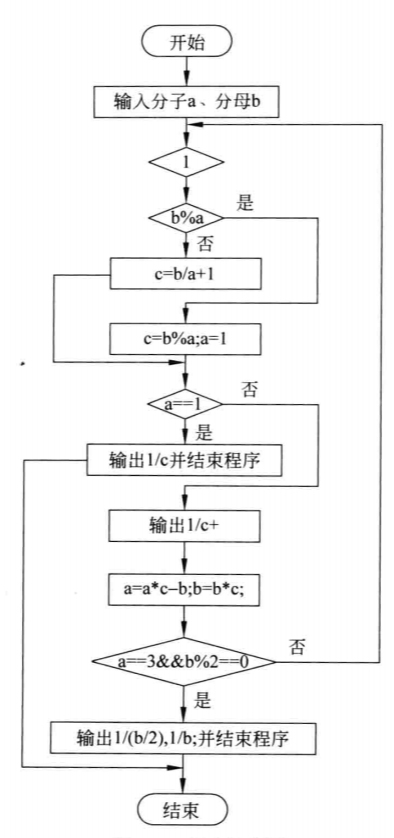
具体代码:
#include<stdio.h>
int main(){
long int a,b,c;
printf("Please enter a optional fraction(a/b):");
scanf("%1d/%1d",&a,&b);
printf("It can be decomposed to:");
while(1){
if(b%a)
c=b/a+1;
else
{
c=b/a;
a=1;
}
if(a==1)
{
printf("1/%1d\n",c);
break;
}
else
printf("1/%1d +",c);
a=a*c-b;
b=b*c;
if(a==3&&b%2==0)
{
printf("1/%1d + 1/%1d\n",b/2,b);
break;
}
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号