ORB-SLAM2 论文&代码学习 —— 单目初始化
转载请注明出处,谢谢
原创作者:Mingrui
原创链接:https://www.cnblogs.com/MingruiYu/p/12358458.html
本文要点:
- ORB-SLAM2 单目初始化部分 论文内容介绍
- ORB-SLAM2 单目初始化部分 代码结构介绍
写在前面
之前的 ORB-SLAM2 系列文章中,我们已经对 Tracking 线程做了介绍,但是当时我们跳过了 Tracking 线程中一个很重要的部分 —— 单目初始化。我们将在本文中,对 ORB-SLAM2 系统的单目初始化部分进行介绍。
依旧祭出该图,方便查看:
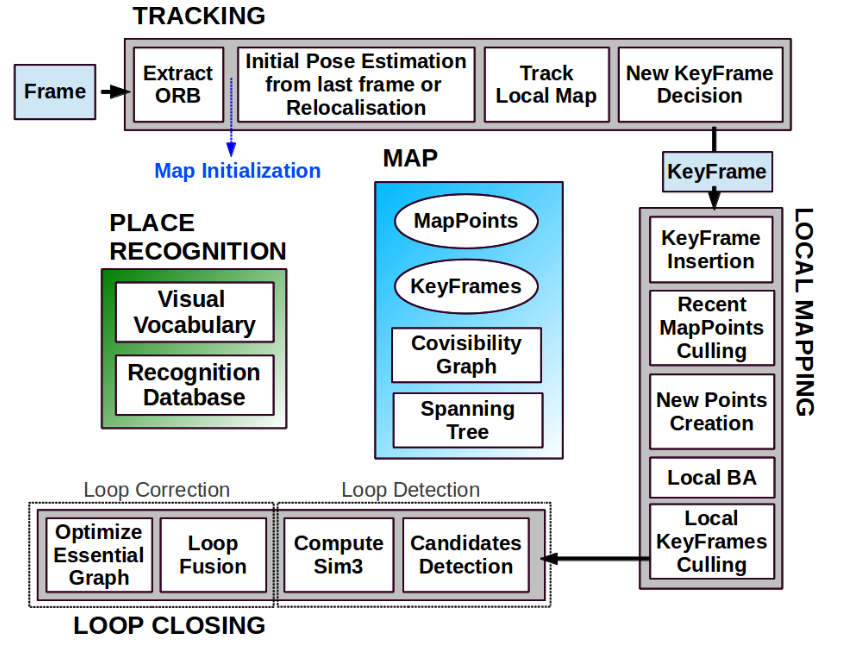
也再次献上我绘制的程序导图全图:ORB-SLAM2 程序导图
老规矩,还是分两部分:以 ORB-SLAM 论文为参考 和 以 ORB-SLAM2 代码(程序导图)为参考。
以 ORB-SLAM 论文为参考
对于任何一个单目 SLAM 系统来说,在系统运行之初都要进行初始化,其目的在于,要计算出某两帧的相对位姿,以此来通过三角化得到一些初始 MapPoints,从而得到一个初始的 Map,这样之后的跟踪也好优化也好都在这个基础上进行。在 ORB-SLAM 之前的单目 SLAM 系统的初始化,往往需要依赖真实场景中某样确定的物体(eg. MonoSLAM)或者需要人工介入(eg. PTAM),而 ORB-SLAM 的单目初始化是完全自动的。
对 SLAM 基础知识有过了解的同学会知道,恢复两帧之间的相对运动,有两种模型:基础矩阵(Fundamental)(等同于本质矩阵)模型和单应矩阵(Homography)模型。正常情况下基础矩阵模型应该可以应付,但如果特征点共面(初始化场景中主要是一个平面),或者两帧之间的相对位姿未纯旋转时,基础矩阵的自由度会下降,也就是所谓的退化,类似于方程数少于变量数。此时为了保证运动恢复的精度,就不能再用基础矩阵模型。由此提出了单应矩阵,其假设特征点落在同一平面上,从而适用于这种场景下的运动恢复。
ORB-SLAM 在初始化时,它也不知道场景中的特征点在不在同一平面,所以它选择两种模型各自算一遍(开两个线程同时算),之后计算两种模型各自进行运动恢复的得分,取得分高的模型,再根据该模型,计算两帧之间的相对位姿并进行初始化。
单目初始化具体步骤
1. 提取 ORB 特征点
在当前帧和参考帧中提取 FeaturePoints(只在最优的尺度),同时将当前帧和参考帧的 FeaturePoints 做匹配。如果匹配点不够多,重新初始化。
2. 同时计算两种模型
- 单应矩阵 \(H_{cr}\):DLT 算法 + RANSAC 迭代
- 基础矩阵 \(F_{cr}\):8点法 + RANSAC 迭代
同时计算两种模型各自的得分,计算公式如下(其中 M 可以表示 H (Homography),也可以表示 F (Fundamental)):
\(S_{M}=\sum_{i}\left(\rho_{M}\left(d_{c r}^{2}\left(\mathbf{x}_{c}^{i}, \mathbf{x}_{r}^{i}, M\right)\right)+\rho_{M}\left(d_{r c}^{2}\left(\mathbf{x}_{c}^{i}, \mathbf{x}_{r}^{i}, M\right)\right)\right)\)
\(\rho_{M}\left(d^{2}\right)=\left\{\begin{array}{ll} {\Gamma-d^{2}} & {\text { if } \quad d^{2}<T_{M}} \\ {0} & {\text { if } \quad d^{2} \geq T_{M}} \end{array}\right.\)
其中 \(d_{c r}^{2}\) \(d_{r c}^{2}\) 是对称转换误差。\(\rho_{M}()\) 的作用是令大的误差对低的得分,其中 \(T_M\) 阈值是算出来的:假设测量值误差的标准差为1像素,通过95%的 \(\chi^{2}\) 检验得到的。对于每种模型,在 RANSAC 迭代过程中保留得分最高的模型。如果最终没能求出解(对于 RANSAC,inliers不够多),则重新初始化。
3. 选择合适的模型
根据两种模型各自的得分:
\(R_{H}=\frac{S_{H}}{S_{H}+S_{F}}\)
如果 \(R_H\) > 0.45(代码中是 0.4),则选用单应矩阵;反之则选基础矩阵模型。大概就是选得分高的,此处的 0.4 应该是经验值。
4. 进行运动恢复,求解两帧相对位姿(\(R, t\))并通过三角化得到初始 MapPoints
在求出 \(H_{cr}\) 或 \(F_{cr}\) 后,就要根据该矩阵求出相对位姿(\(R, t\))。但这个过程的求出的解不是唯一的。ORB-SLAM 采取的筛选办法是:对这些解全部进行三角化恢复 MapPoints,哪个解恢复出来的 MapPoints 大部分都在相机前方且重投影误差小,就选哪个解。如果不能明确选出一个最合适的,则重新初始化。
5. BA 优化
最后,进行一次全局 BA,优化以下,得到最终的初始化结果。
从以上步骤可以看出,ORB-SLAM 在单目初始化花了很多心思。有一个很明显的特点:只要出现一点不妥,ORB-SLAM 就会选择重新初始化。论文中说,这种高标准严要求的初始化准则,是 ORB-SLAM 系统鲁棒性非常好的重要原因之一。因为如果初始化就不合适或出错,后面的跟踪只会一错再错,错上加错。
以 ORB-SLAM2 代码(程序导图为参考)
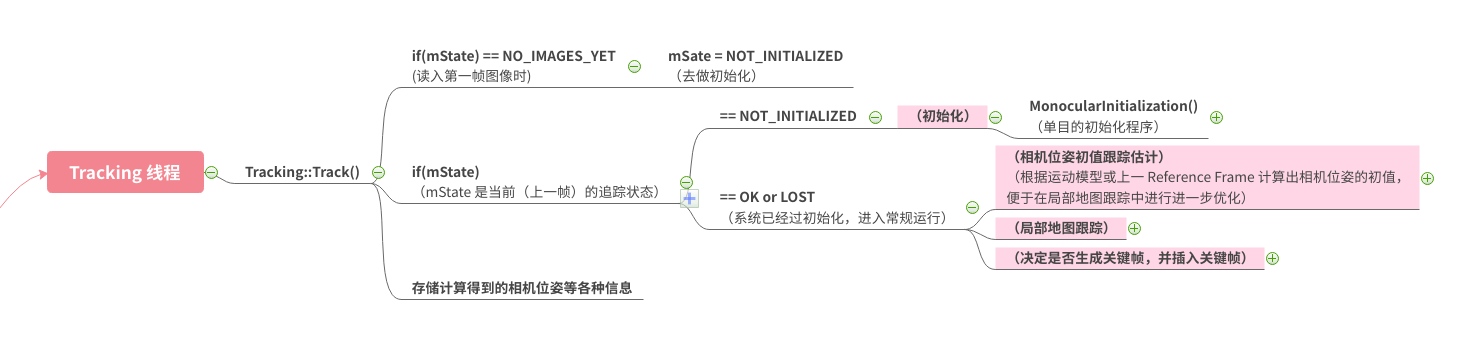
在上图中 MonocularInitialization() 就是初始化的程序,我们可以看到它在 Tracking 线程中的位置。

上图是 MonocularInitialization() 部分的程序框图,其大体和论文中介绍的步骤是完全一致的,这样图已经很清晰了,这里就不多描述了。
如果嫌这张图不够清晰的话,可以点击 ORB-SLAM2 程序导图链接(文首)查看清晰全图
PS: 从中上图我们可以看到,在恢复出两帧之间的相对运动后,程序中还要使用 Tracking::CreateInitialMapMonocular() 来建立初始化的地图。这部分在论文里几乎没有笔墨提到,但在程序里需要很大篇幅来实现。这个细节就反映了我在本系列博文开篇就提到过的读通 ORB-SLAM2 代码的困难之处。以我现在小菜鸡的水平,我根本想象不出 ORB-SLAM2 这样复杂而环环相扣的工程是怎么写出来的(流泪)。




