Hash 算法学习笔记与总结
Hash
哈希算法是通过一个哈希函数 H ,将一种数据（包活字符串、较大的数等）转化为能够用变量表示或是直接就可作为数组下标的数，道过哈希函数转化得到的数值我们称之为哈希值，通过哈希值可以实现快速查找和匹配。以下介绍两种哈希算法的具体运用：字符申 Hash 和哈希表。
字符串 Hash
字符串 Hash 也称 字符串前缀 Hash 法
信息学奥赛一本通
AcWing
\(P = 131 或 13331, Q = 2 ^{64}\) 时，可避免绝大部分的字符串 Hash 值相同的情况。
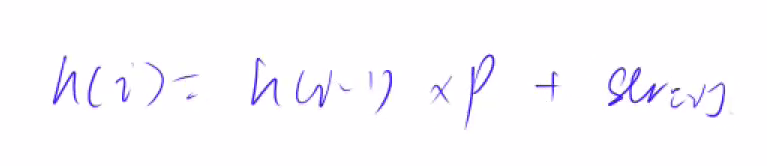
模板
核心思想：将字符串看成P进制数，P的经验值是131或13331，取这两个值的冲突概率低
小技巧：取模的数用2^64，这样直接用unsigned long long存储，溢出的结果就是取模的结果
typedef unsigned long long ULL;
ULL h[N], p[N]; // h[k]存储字符串前k个字母的哈希值, p[k]存储 P^k mod 2^64
// 初始化
p[0] = 1;
for (int i = 1; i <= n; i ++ )
{
h[i] = h[i - 1] * P + str[i];
p[i] = p[i - 1] * P;
}
// 计算子串 str[l ~ r] 的哈希值
ULL get(int l, int r)
{
return h[r] - h[l - 1] * p[r - l + 1];
}
模板题
AcWing 841. 字符串哈希 题目入口
题目大意
给定一个长度为 \(n\) 的字符串，再给定 \(m\) 个询问，每个询问包含四个整数 \(l1,r1,l2,r2\)，请你判断 \([l1,r1]\) 和 \([l2,r2]\) 这两个区间所包含的字符串子串是否完全相同。
字符串中只包含大小写英文字母和数字。
CODE
点击查看代码
// c++11
#include <iostream>
using namespace std;
using ULL = unsigned long long;
const int N = 1e5 + 10, P = 131;
int n, m;
char str[N];
ULL h[N], p[N];
ULL get(int l, int r)
{
return h[r] - h[l - 1] * p[r - l + 1];
}
int main()
{
scanf("%d%d", &n, &m);
scanf("%s", str + 1);
p[0] = 1;
for (int i = 1; i <= n; i ++ )
{
p[i] = p[i - 1] * P;
h[i] = h[i - 1] * P + str[i];
}
while (m -- )
{
int l1, r1, l2, r2;
scanf("%d%d%d%d", &l1, &r1, &l2, &r2);
puts(get(l1, r1) == get(l2, r2) ? "Yes" : "No");
}
return 0;
}
Hash 表
哈希表是一种高效的数据结构它的优点同字符申哈希一样，查找的算法时间效率几平就是常数时间，同时也很容易实现；多产生的代价仅仅是消耗较多的内存。当前比赛可利用的计算机内存越来越大、程序运行时间要求越米越短，用空间换时间的做法还是值得的。
拉链法
(1) 拉链法
// N取比题目范围大的第一个质数更好
int h[N], e[N], ne[N], idx;
// 向哈希表中插入一个数
void insert(int x)
{
int k = (x % N + N) % N;
e[idx] = x;
ne[idx] = h[k];
h[k] = idx ++ ;
}
// 在哈希表中查询某个数是否存在
bool find(int x)
{
int k = (x % N + N) % N;
for (int i = h[k]; i != -1; i = ne[i])
if (e[i] == x)
return true;
return false;
}
开放寻址法
(2) 开放寻址法
// N通常取题目范围的2倍，再找第一个比2N大的质数
int h[N];
// 如果x在哈希表中，返回x的下标；如果x不在哈希表中，返回x应该插入的位置
int find(int x)
{
int t = (x % N + N) % N;
while (h[t] != null && h[t] != x)
{
t ++ ;
if (t == N) t = 0;
}
return t;
}
模板题
AcWing 840. 模拟散列表 题目入口
题目大意
维护一个集合，支持如下几种操作：
I x，插入一个数 \(x\)；Q x，询问数 \(x\) 是否在集合中出现过
现在要进行 \(N\) 次操作，对于每个询问操作输出对应的结果。
CODE
点击查看代码 - 拉链法
//拉链法
#include <bits/stdc++.h>
using namespace std;
const int N = 100003; // 大于100000的第一个质数
int h[N], e[N], ne[N], idx;
void insert(int x)
{
int k = (x % N + N) % N; // 哈希
// 建立链表
e[idx] = x;
ne[idx] = h[k];
h[k] = idx ++ ;
}
bool find(int x)
{
int k = (x % N + N) % N; // 哈希
for(int i = h[k]; ~i; i = ne[i]) // 遍历链表
if(e[i] == x)
return true;
return false;
}
int main()
{
int n;
scanf("%d", &n);
memset(h, -1, sizeof h); // 指向空节点
while (n -- )
{
char op[2];
int x;
scanf("%s%d", op, &x);
if(*op == 'I')
insert(x);
else
puts(find(x) ? "Yes" : "No");
}
}
点击查看代码 - 开放寻址法
// 开放寻址法
#include <bits/stdc++.h>
using namespace std;
const int N = 200003; // 2N后找质数
const int null = 0x3f3f3f3f; // 无穷大
int h[N];
int find(int x)
{
int k = (x % N + N) % N; // 哈希
while(h[k] != null && h[k] != x) // 找坑位
{
k ++ ;
if(k == N)
k = 0;
}
return k; // 应该放x的位置
}
int main()
{
int n;
scanf("%d", &n);
memset(h, 0x3f, sizeof h); // 初始化为null=0x3f3f3f3f，正无穷
while(n -- )
{
char op[2];
int x;
scanf("%s%d", op, &x);
int k = find(x);
if(*op == 'I')
h[k] = x;
else
puts(h[k] != null ? "Yes" : "No");
}
return 0;
}
