二分算法学习笔记与总结
二分
二分查找 侧重于查找一个元素是否存在，而 二分答案 则侧重于找到答案。
二分原理
二分，分而为二。
二分算法，顾名思义，就是把一组有序数据的搜索区域缩小一半。
整数二分
二分查找原理
将搜索区域按是否满足条件 check() 缩小一半
根据情况可能存在两种情况
对于区间 \(\left[ l, r \right]\) ， \(mid\) 为中点：
- \(\left[ l, mid \right]\) 与 \(\left[ mid + 1, r \right]\) ，此时 \(mid = \lfloor \cfrac{l + r}{2} \rfloor\)
- \(\left[ l, mid - 1 \right]\) 与 \(\left[ mid, r \right]\) ，此时 \(mid = \lceil \cfrac{l + r}{2} \rceil\)
注意： 情况1为下取整，情况2为上取整。
情况 1 下取整： C++ 自动下取整
情况 2 上取整： 当 \(l=r-1\) 时， \(mid=\lfloor \cfrac{l + r}{2} \rfloor = l\)，此时左区间为 \(\left[ l, l - 1 \right]\)。下一次迭代时会出现问题 \(l > r\)，将导致程序故障或 死循环。
二分查找模板
AcWing 模板入口
模板一
- \(\left[ l, mid \right]\) 与 \(\left[ mid + 1, r \right]\) ，此时 \(mid = \lfloor \cfrac{l + r}{2} \rfloor\)
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid;
else l = mid + 1; // +1
}
return l;
}
模板二
- \(\left[ l, mid - 1 \right]\) 与 \(\left[ mid, r \right]\) ，此时 \(mid = \lceil \cfrac{l + r}{2} \rceil\)
int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = l + r + 1 >> 1; // +1
if (check(mid)) l = mid;
else r = mid - 1; // -1
}
return l;
}
有 -1 必 +1
二分结束后，左端点将等于右端点，即 l == r
分析题目时，从 check() 入手，再判断使用哪一个模板
二分查找一定有解（一定可求出边界）
二分查找用法
有单调性就可以二分
二分不一定非得有单调性
二分的本质：寻找边界——满足条件的边界（左右）
题目1 （模板）（二分查找）
AcWing 789. 数的范围 题目入口
题目大意
给定一个按照升序排列的长度为 \(n\) 的整数数组，以及 \(q\) 个查询。
对于每个查询，返回一个元素 \(k\) 的起始位置和终止位置（位置从 $0 开始计数）。
如果数组中不存在该元素，则返回 -1 -1 。
题目分析
这是一道经典的模板题
包含两个模板，需要两次二分。
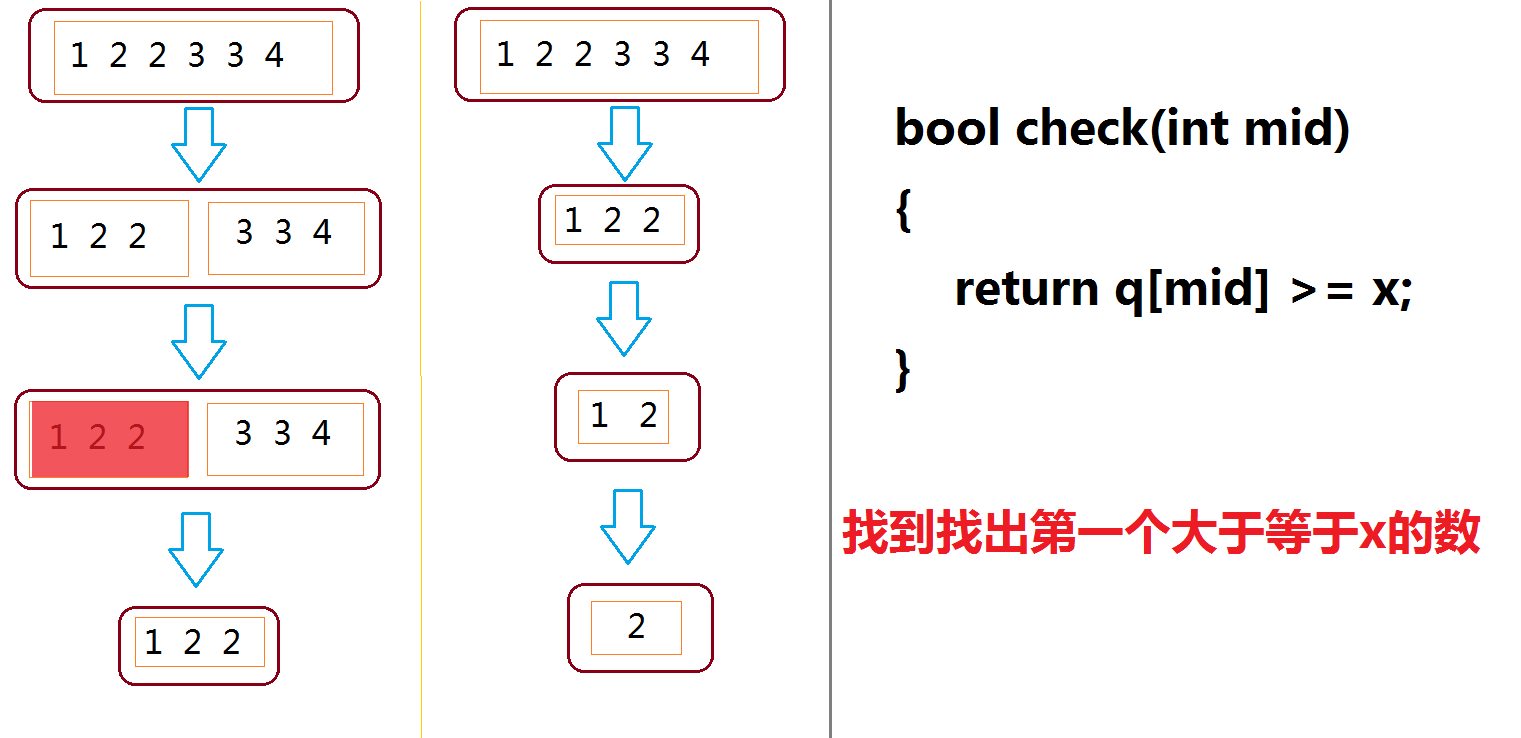
第一次找出第一个小于等于 \(k\) 的数，第二次找出大于等于 \(k\) 的数。
第一次二分查找过程（图片中 x 表示 \(k\)）
第二次同理
当第一次二分结束后，如果 l 或 r 指向的数不等于 \(k\)，则表明此数组中不存在 \(k\)。
点击查看二分模板
模板一
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid;
else l = mid + 1; // +1
}
return l;
}
模板二
int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = l + r + 1 >> 1; // +1
if (check(mid)) l = mid;
else r = mid - 1; // -1
}
return l;
}
CODE
Code1 手打模板
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int n, T;
int q[N];
int main()
{
scanf("%d%d", &n, &T);
for (int i = 0; i < n; i ++ )
scanf("%d", &q[i]);
while (T -- )
{
int x;
scanf("%d", &x);
int l = 0, r = n - 1; // 模板一
while (l < r)
{
int mid = l + r >> 1; // (l + r) / 2
if (q[mid] >= x) r = mid; // 找出第一个 <=x 的数
else l = mid + 1;
}
/* 此时 l = r */
if (q[l] != x) // 说明数组中不存在 x
{
puts("-1 -1");
continue;
}
else printf("%d ", l);
l = 0, r = n -1; // 模板二
while (l < r)
{
int mid = l + r + 1 >> 1; // 有 r = mid - 1，所以需要上取整
if (q[mid] <= x) l = mid; // 找出第一个 >=x 的数
else r = mid - 1;
}
printf("%d\n", l);
}
return 0;
}
Code2 STL 实现
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, T;
int q[N];
int main()
{
scanf("%d%d", &n, &T);
for (int i = 0; i < n; i ++ )
scanf("%d", &q[i]);
while (T -- )
{
int x;
scanf("%d", &x);
int _l = lower_bound(q, q + n, x) - q; // 第一个大于等于x的数的下标
if (q[_l] != x) // 不存在x
{
puts("-1 -1");
continue;
}
int _r = upper_bound(q, q + n, x) - q; // 第一个大于x的数的下标
printf("%d %d\n", _l, _r - 1);
}
return 0;
}
题目2 （运用）（二分查找）
洛谷 P1102 A-B 数对 题目入口
题目大意
给出一串有 \(n\) 个正整数的正整数数列以及一个正整数 \(C\)，要求计算出所有满足 \(A - B = C\) 的数对的个数（不同位置的数字一样的数对算不同的数对）。
题目分析
将 \(A - B = C\) 转为 \(A + C = B\).
所以只需要从 \(1\) 至 \(n\) 枚举 \(A\)
CODE
Code1 手打模板
#include <bits/stdc++.h>
#define int long long // 本题范围可能爆longlong
using namespace std;
const int N = 2e5 + 10;
int n, c;
int a[N];
int ans;
signed main()
{
cin >> n >> c;
for (int i = 1; i <= n; i ++ )
cin >> a[i];
sort(a + 1, a + n + 1); // 使数组具有单调性
for (int i = 1; i <= n; i ++ )
{
int x = a[i] + c;
int l = 1, r = n;
while (l < r) // 模板一
{
int mid = l + r >> 1;
if (a[mid] >= x) r = mid;
else l = mid + 1;
}
if (a[l] != x) continue; // 不存在x
int _r = l; // 记录左端点
l = 1, r = n;
while (l < r) // 模板二
{
int mid = l + r + 1>> 1;
if (a[mid] <= x) l = mid;
else r = mid - 1;
}
ans += l - _r + 1;
}
cout << ans << endl;
return 0;
}
Code2 STL 实现
#include <bits/stdc++.h>
#define int long long // 本题范围可能爆longlong
using namespace std;
const int N = 2e5 + 10;
int n, c;
int a[N];
int ans;
signed main()
{
cin >> n >> c;
for (int i = 1; i <= n; i ++ )
cin >> a[i];
sort(a + 1, a + n + 1); // 单调性
for (int i = 1; i <= n; i ++ )
ans += (upper_bound(a + 1, a + n + 1, a[i] + c) - a) - (lower_bound(a + 1, a + n + 1, a[i] + c) - a);
cout << ans << endl;
return 0;
}
STL 中的二分查找
最详讲解
lower_bound, upper_bound, greater, less 用法
lower_bound() 和 upper_bound 这两个函数是 STL 中用于二分查找的两个函数。
包含于头文件 algorithm，即 #include<algorithm>
lower_bound()
对于 lower_bound(begin, end, key) 返回值是一个 迭代器 在区间 \(\left [ begin, end\right )\) 返回指向大于等于 key 的第一个值的 位置。
其中，begin 和 end 是 地址，key 是 值，lower_bound() 的返回值是 地址
对于有一个有序的数组 \(a\)，并将数 \(x\) 作为二分查找的目标。
lower_bound(a, a + n, x) - a; //下标从0开始
lower_bound(a + 1, a + n + 1, x) - a; //下标从1开始
它们就能取得 最小 的 \(a\) 数组的下标 \(i\)，满足 \(a_i \geq x\)。
lower_bound() 返回值是地址，减去数组名（数组名同时是指向数组头的指针）即为下标
upper_bound()
upper_bound() 与 lower_bound() 用法一致。
对于有一个有序的数组 \(a\)，并将数 \(x\) 作为二分查找的目标。
upper_bound(a, a + n, x) - a; //下标从0开始
upper_bound(a + 1, a + n + 1, x) - a; //下标从1开始
它们就能取得 最小 的 \(a\) 数组的下标 \(i\)，满足 \(a_i>x\)。
浮点二分
浮点数二分模板
bool check(double x) {/* ... */} // 检查x是否满足某种性质
double bsearch_3(double l, double r)
{
const double eps = 1e-6; // eps 表示精度，取决于题目对精度的要求
while (r - l > eps)
{
double mid = (l + r) / 2;
if (check(mid)) r = mid;
else l = mid;
}
return l;
}
注意： 因为是浮点数，所以不需要 +1 或 -1, 不能使用 >> 1
浮点数二分答案模板题目
AcWing 790. 数的三次方根 题目入口
更多题目
