最短路算法 Dijkstra 入门
dijkstra算法 是一种单源点最短路算法求出一个点到其他所有点的最短路。
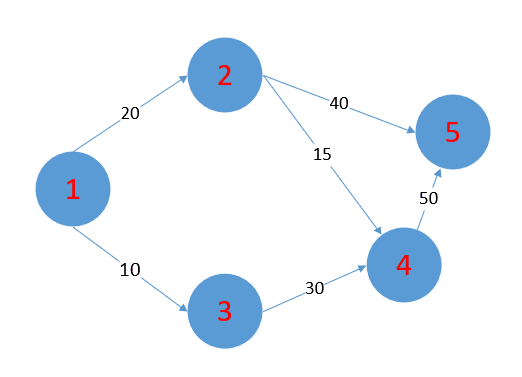
给你这样的一个图，需要求出1号点到其他点的最短距离是多少。
首先我们开一个数组 d[N]，d[x] 代表着从起点出发到x点的距离是多少。
开一个数组vis[N], vis[x]数组代表着某个点d[x]是不是成为定值，不会再变小了。
然后我们在开一个数组，edge[N][N]，edge[a][b] 代表着从a点走到b的路程是多少。
如果不存在 a->b的这条边，那么就将他设置为-1。
更新d数组的条件：d[a] > d[b] + edge[b][a] 的时候更新d[a]的值。
一开始我们将所有距离设置都设置 inf ( inf 意为无穷大）。
当然d[s] = 0;
所以对于刚开始的数组d[]来说他的值应该为
图的状态应该是
现在我们从1号点出发，图上存在一个 1->3的边 距离为 10 存在一个1->2的边 距离为20。
那么d[3] = min(d[3], d[1] + edge[1][3]) d[2] = min(d[2], d[1] + edge[1][2])
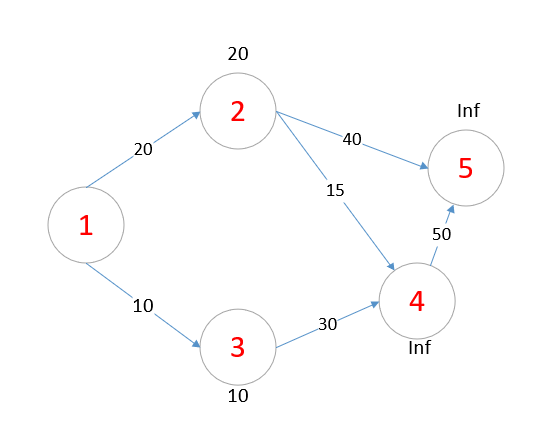
d数组即被更新成
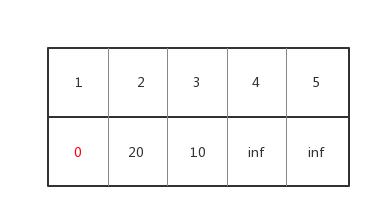
其中vis[1] = 1，即这个点不会的距离不会在变小了。
我们扫一遍d数组，跳过vis[x] == 1的点，找到d[x]最小的点，通过上面的那个数组我们可以发现，这个点是3，
我们把 vis[3] = 1， 然后再通过3号点出发更新d[].
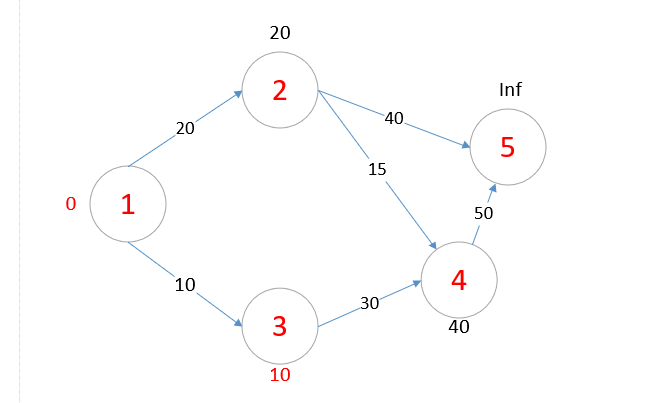
d数组的值为
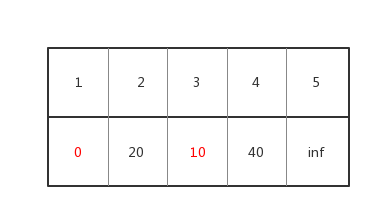
然后我们继续找到d[x]最小的且没被标记过的点 由上表可知是点2
我们标记点2，然后再用2号点出发，看看有没有点的距离可以被更新成更小的。
当我们走完2号点的边的时候，图就会变成
d数组的结果为
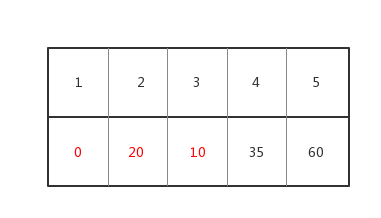
我们继续找到d[x]最小的且没被标记过的点 由上表可知是点4
我们先标记4号点，然后通过点4出发，然后看一下出4号点出发，有没有点的d会被更新成更小的值
d数组的结果为
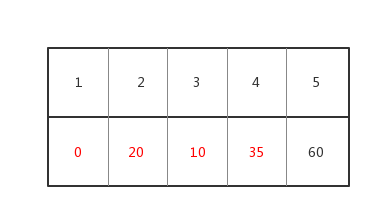
最后没标记过的点只有5了， 我们从5号点出发，看看有没有点会继续被更新。
我们得到最后的图就变成了
d数组最后就被更新成了
这样我们就进行完了dijkstra算法。
从原点出发到各个点的最短路径是多少就求出来了。
假设 d[a] < d[b] ， 并且存在edge[a][b] ， 那么因为边edge[a][b] > 0，那么不可能通过 b 点去更新 a 点， 只可能从a点出发然后到b点，使得d[b]的更小。
因为更新的条件是 d[b] > d[a] + edge[a][b]。 所以只有从d[]更小的点出发才有可能使得别的点更小。
总结下来的话，就是从原点出发，每次都选出当前距离里原点最近的点(跳过标记过的点）x，然后从x点出发，遍历x点的所有边，看一下是不是存在别的点可以通过点x往外走，使得原点到目标点的距离更小，并且标记一下点x，下次不会再选择x，因为x已经是最小的了。
每次都确立一个点，确立完一个点后需要其访问所有点去更新距离，总有由n个点
所以 时间复杂度是 n * 2n
来一个题目：
1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 #include<algorithm> 5 using namespace std; 6 int edge[100+5][100+5]; 7 int d[100+5]; 8 bool vis[100+5]; 9 const int inf = 0x3f3f3f3f; 10 int main() 11 { 12 int n, m; 13 while(~scanf("%d%d",&n,&m)&& (n || m)){ 14 int a,b,c; 15 memset(edge, -1, sizeof(edge)); 16 memset(d, inf, sizeof(d)); 17 memset(vis, 0, sizeof(vis)); 18 while (m--){ 19 scanf("%d%d%d", &a, &b, &c); 20 edge[a][b] = edge[b][a] = c; 21 } 22 for(int i = 2;i <= n;i++ ){ 23 if(edge[1][i] == -1) continue; 24 d[i] = edge[1][i]; 25 } 26 d[1] = 0; 27 vis[1] = 1; 28 while (1){ 29 int min1 = inf,z = -1; 30 for (int j = 1;j <= n; j++) 31 if(!vis[j] && min1 > d[j]) 32 z = j, min1 = d[j]; 33 if(z == -1) break; 34 vis[z] = 1; 35 for (int j = 1; j <= n ; j++){ 36 if(edge[z][j] == -1) continue; 37 d[j] = min(d[j], d[z] + edge[z][j]); 38 } 39 } 40 printf("%d\n", d[n]); 41 } 42 return 0; 43 }
现在这个是时空复杂度最高的代码。
接来下还有关于dijkstra优化的传送门。
