LeetCode 59. 螺旋矩阵 II

LeetCode 59. 螺旋矩阵 II 题目跳转链接

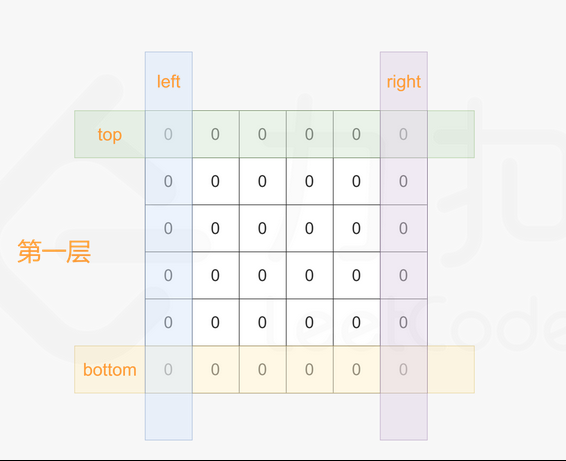
这道题可以采用模拟法来实现。我们可以设置上下左右四个边界，然后模拟螺旋填充元素。具体来说，我们定义 left、right、top、bottom 四个变量代表当前需要填充的最左边、最右边、最上面、最下面的位置，然后根据当前位置，依次填充矩阵。

具体可以按照以下步骤实现：

1. 初始化矩阵 matrix，并且初始化 left、right、top、bottom 四个变量的值；

2. 当 left⩽right 且 top⩽bottom 时，执行以下步骤：

2.1 从左往右填充 matrix[top][left] 至 matrix[top][right] 的所有元素；

2.2 从上往下填充 matrix[top+1][right] 至 matrix[bottom][right] 的所有元素，注意需要判断 top<bottom，否则在第一行和第一列填满后会在第二行和第二列重复填充；

2.3 从右往左填充 matrix[bottom][right−1] 至 matrix[bottom][left] 的所有元素，注意需要判断 left<right，否则在第一列填满后会在第二列重复填充；

2.4 从下往上填充 matrix[bottom−1][left] 至 matrix[top+1][left] 的所有元素，注意需要判断 top<bottom−1，否则在第一行填满后会在第二行重复填充；

3. 循环结束后，返回 matrix 即可。

这样，我们就可以用 O(n2) 的时间复杂度和 O(1) 的空间复杂度完成矩阵的填充任务。

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) 
    {
        vector<vector<int>> matrix(n,vector<int>(n));
        int left=0,right=n-1,top=0,bottom=n-1;
        int num=1;
        while(left<=right&&top<=bottom)
        {
            //从左向右填充
            for(int i=left;i<=right;i++)
            {
                matrix[top][i]=num;
                num++;
            }
            top++;
   // 从上向下填充
            for(int i=top;i<=bottom;i++)
            {
                matrix[i][right]=num;
                num++;
            }
            right--;

            // 从右向左填充
            if(left<=right&& top<=bottom)  //注意这里 
            {
                for(int i=right;i>=left;i--)
                {
                    matrix[bottom][i]=num;
                    num++;
                }
                bottom--;
            }

             // 从下向上填充
            if(left<=right&&top<=bottom)
            {
                for(int i=bottom;i>=top;i--)
                {
                    matrix[i][left]=num;
                    num++;   
                }
                    left++;
            }
        }
        return matrix;


    }
};
      

虽然 vector<vector> matrix(n, vector(n)) 定义了一个 n × n 的二维 vector，但整个矩阵填充的过程只使用了常数个额外的变量和常量个大小为 n 的变量，而不使用额外的数组或 vector，因此空间复杂度为 O(1)。

另一种模拟 空间复杂度更高点

题目要求生成一个按照螺旋顺序排列的 n×n 矩阵，我们可以采用模拟的方法来实现。

具体思路如下：

• 我们定义四个变量 top、bottom、left、right 分别表示当前填充区域的上边界、下边界、左边界、右边界；
• 初始时，top=0、bottom=n−1、left=0、right=n−1；
• 从左到右填充最上面一行，然后将 top 变量自增；
• 从上到下填充最右边一列，然后将 right 变量自减；
• 从右到左填充最下面一行，然后将 bottom 变量自减；
• 从下到上填充最左边一列，然后将 left 变量自增；
• 重复上述步骤，直到所有位置填充完毕。
  算法最终返回生成的矩阵。

上述思路中关键是确定好几个变量的初始值和更新时机。在更新边界变量的时候，需要判断边界是否相遇，否则在矩阵周围有一圈元素尚未填充时会出现重复填充的情况。

时间复杂度：O(n2)，需要遍历整个 n×n 的矩阵。
空间复杂度：O(n2)，需要使用一个大小为 n×n 的矩阵。

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        int t = 0;      // top
        int b = n-1;    // bottom
        int l = 0;      // left
        int r = n-1;    // right
        vector<vector<int>> ans(n,vector<int>(n));
        int k=1;
        while(k<=n*n){
            for(int i=l;i<=r;++i,++k) ans[t][i] = k;
            ++t;
            for(int i=t;i<=b;++i,++k) ans[i][r] = k;
            --r;
            for(int i=r;i>=l;--i,++k) ans[b][i] = k;
            --b;
            for(int i=b;i>=t;--i,++k) ans[i][l] = k;
            ++l;
        }
        return ans;
    }
}