Leectcode 63 不同路径II

力扣 题目跳转链接

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

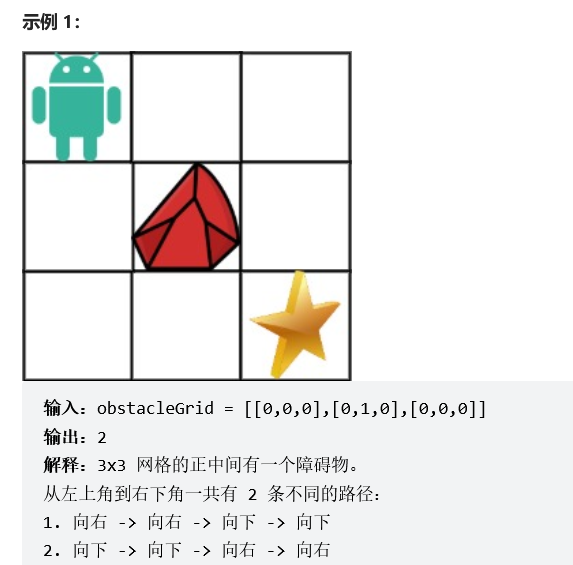
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

代码随想录_不同路径II

dp[i][j] ：表示从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径。
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。

因为从(0, 0)的位置到(i, 0)的路径只有一条，所以dp[i][0]一定为1，dp[0][j]也同理。

但如果(i, 0) 这条边有了障碍之后，障碍之后（包括障碍）都是走不到的位置了，所以障碍之后的dp[i][0]应该还是初始值0。

dp数组如何初始化

vector<vector<int>> dp(m, vector<int>(n, 0));
  //obstacleGrid[i][0]==0 表示没有障碍物
        for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
        for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;

注意代码里for循环的终止条件，一旦遇到obstacleGrid[i][0] == 1的情况就停止dp[i][0]的赋值1的操作，dp[0][j]同理

class Solution
 {
 
 
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid)
     {
         int m=obstacleGrid.size();
         int n=obstacleGrid[0].size();
 
        // //如果在起点或终点出现了障碍，直接返
        if(obstacleGrid[m-1][n-1]==1||obstacleGrid[0][0]==1) 
        {return 0;}
 
         vector<vector<int>> dp(m,vector<int>(n,0));
         
         //obstacleGrid[i][0]==0 表示没有障碍物
         for(int i=0;i<m&&obstacleGrid[i][0]==0;i++) 
         {
             dp[i][0]=1;
         }
         for(int j=0;j<n&&obstacleGrid[0][j]==0;j++) 
         {
             dp[0][j]=1;
         }
        for(int i=1;i<m;i++)
        {
            for(int j=1;j<n;j++ )
            {
                if(obstacleGrid[i][j]==1) continue;
                dp[i][j]=dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
 
    }
};
 

时间复杂度：O(n × m)，n、m 分别为obstacleGrid 长度和宽度
空间复杂度：O(n × m)