CNN中的卷积操作与参数共享

卷积神经网络（Convolutional Neural Networl, CNN）的两大核心思想：

• 局部连接（Local Connectivity）
• 参数共享（Parameter Sharing）

两者共同的一个关键作用就是减少模型的参数量，使运算更加简洁、高效，能够运行在超大规模数据集上。

局部连接与卷积

图像的局部相关性

对于一张输入图片，大小为$W \times H$，如果使用全连接网络，生成一张$X \times Y$的特征图，需要$W \times H \times X \times Y$个参数，如果原图长宽分别是$10^2$级别的，而且XY大小和WH差不多的话，那么这样一层网络需要的参数个数是$10^8\~10^{12}$级别。

下图展示了全连接网络中一个神经元的参数量。不进行局部连接，每个神经元和每一个输入像素连接，参数量动辄千万级别，网络很难训练：

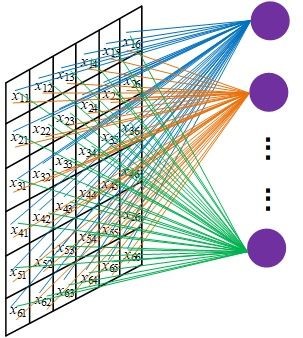
这么多参数肯定是不行的，我们就想办法减少参数的个数。一般而言，图像信息都是局部相关的，如果输入层的每一个像素只和输入层图片的一个局部相连，那么需要的参数个数就可以大大减少。假设输出层每个像素只与输入图片上$F \times F$的一个方块区域有连接，也就是说输入层的这个像素值，只是通过原图的这个$F \times F$的小方形区域中的像素值计算而来，那么对于输出层的每个像素，需要的参数个数就从原来的$W \times H$减少到了$F \times F$。如果对于原图片的每一个$F \times F$的方块都需要计算这样一个输出值，那么需要的参数只是$X \times Y \times F \times F$，如果原图长宽是$10^2$级别，且$F$在$10$以内的话，那么需要的参数个数只有$10^5\~10^6$级别，相比于原来的$10^8\~10^{12}$小了很多很多。

由此，CNN中的局部连接通过卷积操作来实现，避免了全连接中参数过多而造成无法计算的情况。那么，卷积具体是如何运算的呢？

什么是卷积？

卷积运算的本质是卷积核（也可称为滤波器，filter）和输入数据（图像）的局部区域间的点积运算，可以用相应的矩阵乘法来实现。

下图很好地演示了CNN中一个卷积核在单张图像数据上的卷积操作，可以简要地概括为：一个$3 \times 3$大小的卷积核在一张$6 \times 6$大小的输入图像上从左到右、从上到下依次扫描，进行矩阵的点积运算，得到相应位置的运算结果并输出（图中的$x$为输入像素值，$a$为卷积核参数，$F$为输出的运算结果）。

以上是输入为单通道（即二维矩阵）时的情况，当输入是多通道（即三维张量）时，卷积核也相应地“升级”为三维。下图的输入为三通道R(red)G(green)B(blue)图像，分别用不同的三维卷积核（Filter w0，w1）来进行卷积操作：

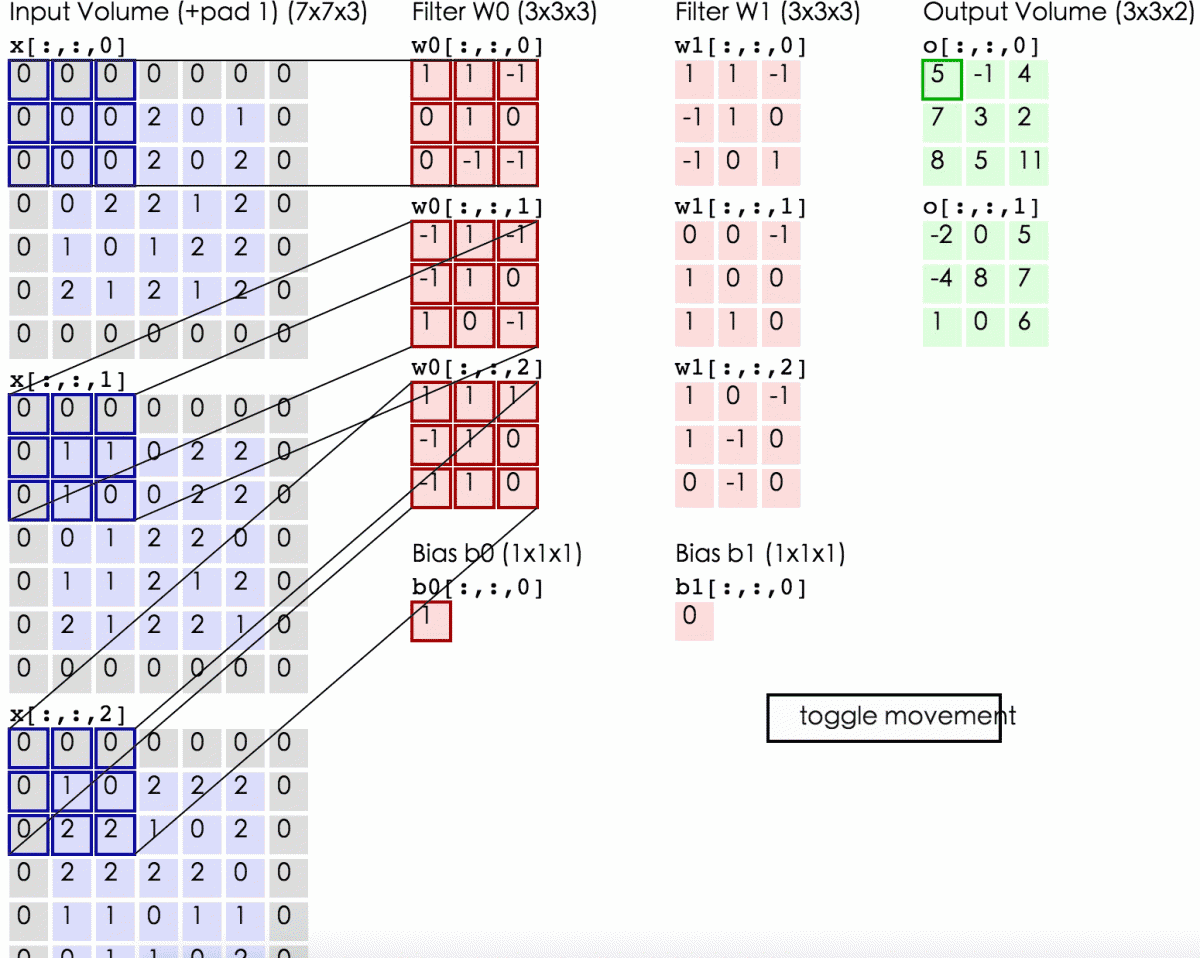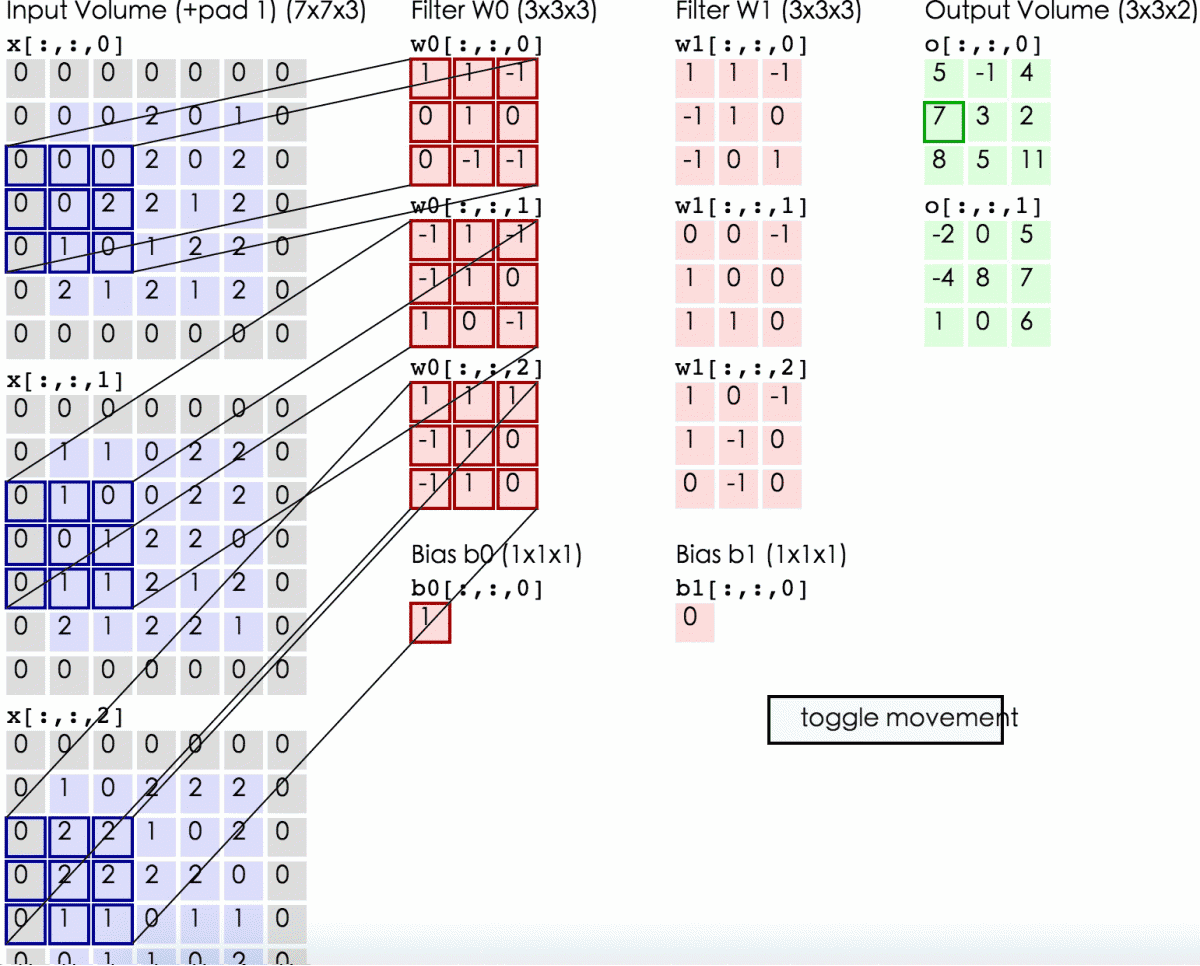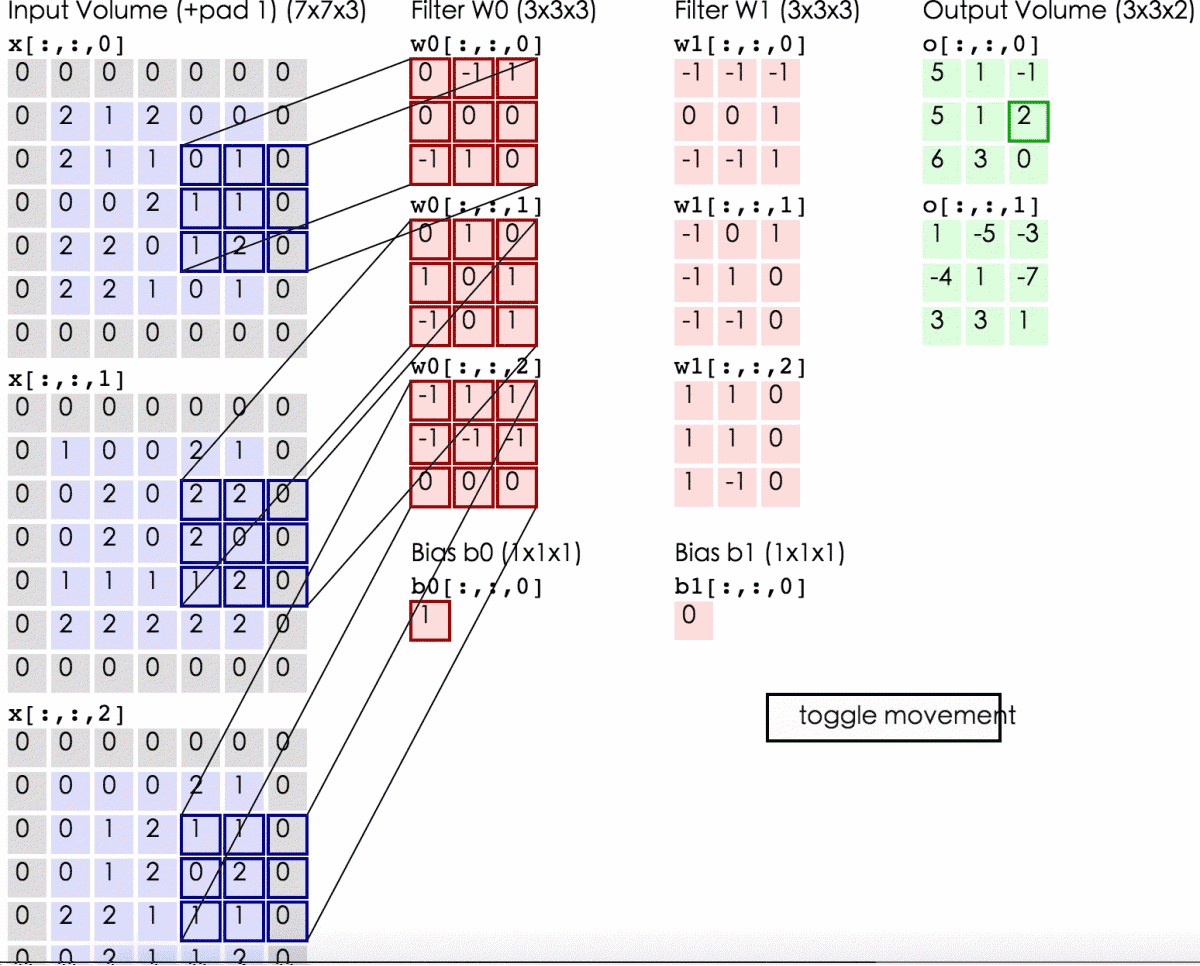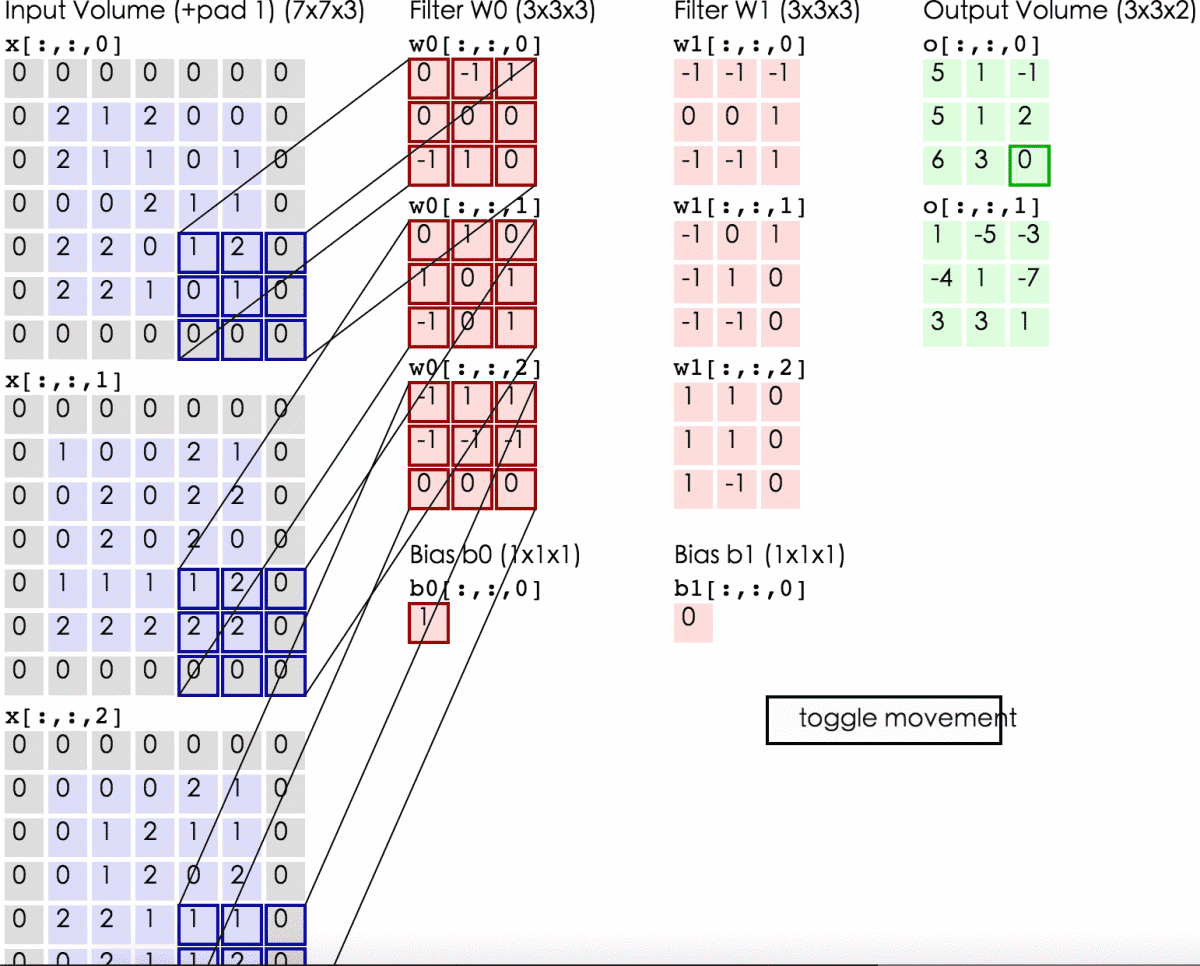
不同的卷积核（filter）

为什么要设置不同的filter呢？因为不同的filter会得到不同的输出数据，对应图像的不同特征信息，比如颜色深浅、轮廓等等。如下图，中间是图像输入，四角分别对应四个filter（带着一组固定权重的神经元）的输出：

下图的卷积层有两个filter，输出两个特征图：

其中输入图像为$32*32*3$，$32$表示图像尺寸，$3$表示它的深度（即RGB三个channel）。卷积层的两个filter均为$5*5*3$（filter的深度必须和输入图像的深度相同），输出的两个特征图均为$28*28*1$。

CNN中的参数共享

卷积核的参数实际上也可以叫做权重，它描述了局部连接中该位置的输入对于相应输出的影响力（重要性）。

图像底层特征的位置无关性

通过卷积操作，我们实现了输入图像的局部连接，从而大大减少了网络模型中的参数量。但这还不够，利用图像的另一特性，参数量可以进一步降低。

卷积中不做参数共享，则每一个输出对应一组参数值，参数量仍然庞大：

我们知道，图像的底层特征是跟具体位置无关的，比如边缘。无论是在图像中间的边缘特征，还是图像四角的边缘特征，都可以用类似于微分的特征提取器提取。那么，对于主要用于提取底层特征的前几层网络，把上述局部全连接层中每一个$F \times F$方形区域对应的参数（权值）共享，就可以进一步减少网络中的参数个数了。也就是说，输出层的每一个像素，是由输入层对应位置的$F \times F$的局部图片，与相同的一组$F \times F$的参数（权值）做内积（点积），再经过非线性单元计算而来的。这样的话，无论图片原大小如何，只用$F \times F$个参数就够了，也就是几个几十个的样子。当然，一组$F \times F$的参数只能得到一张输出特征图，一般会有多组参数，分别经过卷积后可以有好几层特征图。

需要注意的是，高层特征一般是与位置有关的（全局特征），比如 一张人脸图片，眼睛和嘴的位置不同，那么处理到高层，不同位置就需要不同的神经网络权重（参数），这时候卷积层就不能胜任了，就需要用局部全连接层和全连接层。 

示例（一维向量）

共享，即使用同一组参数（权重）来做卷积，如上图。

输入层：$x = [x_1, x_2, x_3, x_4, x_5. x_6, x_7]$

隐藏层：$h = [h_1, h_2, h_3]$

权重向量：$w = [w_1, w_2, w_3] = [1, 0, -1]$

权重值$w$被$h_1, h_2, h_3$共享：$$\begin{align} h_1 &= w \cdot x[1 : 3] \\ h_2 &= w \cdot x[3 : 5] \\ h_3 &= w \cdot x[5 : 7]\end{align}$$

关于卷积神经网络的发展史等更全面介绍推荐这篇：CNN（卷积神经网络）入门，简洁清晰。

（整理自网络）

参考资料

https://blog.csdn.net/qq_40962368/article/details/82864606

https://www.zhihu.com/question/47158818