斐波那契数列的四种解法（头递归、尾递归、迭代与矩阵快速幂）

斐波那契数列

斐波那契数列指的是这样一个数列：

$0, 1, 2, 3, 5, 8, 13, 21...$

后面的每一个数是前面紧邻的两个数之和。

$$F(n) = \begin{cases} 0, &n = 0 \\ 1, &n = 1 \\ F_{n-1} + F_{n-2} &n \ge 2\end{cases}$$

【注意：斐波拉契数列第26个突破十万，第31个突破一百万，第36个突破一千万，第40个突破一亿，第45突破10亿，第50突破100亿。（数列从坐标1开始计数）

由于数列增长快，int类型只能覆盖到近50位，所以尽可能采用long long类型来存储数据。】

通项公式

斐波那契有一个通项公式：$$F(n) = \frac{1}{\sqrt{5}} \times \left[ (\frac{1 + \sqrt{5}}{2}) ^n - (\frac{1 + \sqrt{5}}{2})^n\right]$$

头递归实现（C）

//时间复杂度O(N^2)
//空间复杂度O(N)
long long fib(size_t n) {
    return (n < 2) ? n : (fib(n - 1) + fib(n - 2));
}

递归树

 

从图中可以看出：计算F(10)要计算F(9)和F(8)，而要计算F(9)，又要计算F(8)，以此类推，要计算很多重复的值，这样就浪费了时间，而计算重复值的数量随着N值而急剧增大，事实上该算法的时间复杂度随着n值呈指数增长。不信，大家可以取N = 100看看递归要慢到什么程度。

缺点

（1）只适用于n比较小的时候，否则效率低，因为会做很多次重复操作；
（2）该例递归属于多分支递归，容易造成栈溢出；

尾递归实现（C）

//时间复杂度O(N)
long long fib(long long first, long long second, size_t n)
{
    if(n<2) {
        return n;
    }
    if(2 == n) {
        return first+second；
    }
    return fib(second, first+second, n-1);
}

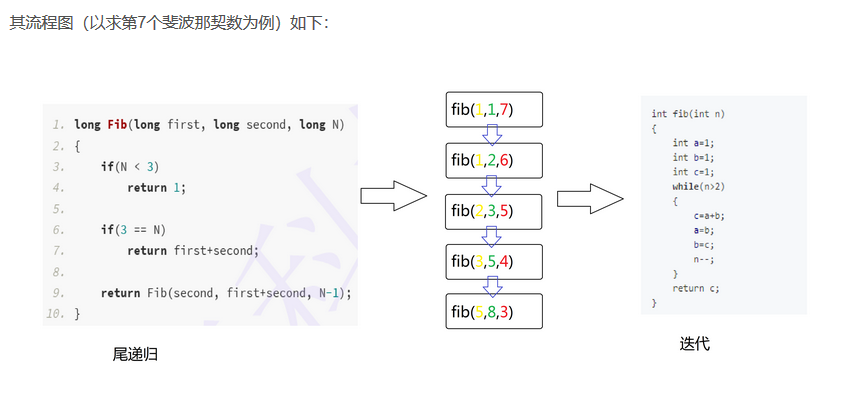
优点

（1）计算结果参与到下一次的计算，从而减少很多重复计算量；

（2）原本朴素的递归产生的栈的层次像二叉树一样，以指数级增长，但是现在栈的层次却像是数组，变成线性增长了。简单来说，原本栈是先扩展开，然后边收拢边计算结果，现在却变成在调用自身的同时通过参数来计算；

（3）部分编译器对于尾递归有特别进行优化，可以提升性能；

总结

尾递归的本质是：将单次计算的结果缓存起来，传递给下次调用，相当于自动累积。

尾递归可以转换成迭代算法。

迭代实现（C）

//时间复杂度O(N)
//空间复杂度O(1)
long long fib(size_t n) {
    long long n1 = 0, n2= 1, n3=n;
    int i = 0;
    for(i = 2;i<=n;i++) {
        n3 = n1+n2;
        n1 = n2;
        n2 = n3;
    }
    return n3;
}

矩阵乘法实现（矩阵快速幂）

关于矩阵快速幂的详细介绍见矩阵快速幂详解一文，斐波拉契数列作为快速幂的一个经典应用，这里直接上公式：

公式

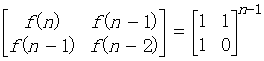
代码实现（C++）

#include<iostream>
#include<string>
using namespace std;
 
 //定义2×2矩阵；
struct Matrix2by2 {
     //构造函数
     Matrix2by2(
         long m_00,
         long m_01,
         long m_10,
         long m_11
     ) :m00(m_00), m01(m_01), m10(m_10), m11(m_11) {}
 
     //数据成员
     long m00;
     long m01;
     long m10;
     long m11;
 };
 
 //定义2×2矩阵的乘法运算
Matrix2by2 MatrixMultiply(const Matrix2by2& matrix1,const Matrix2by2& matrix2) {
     Matrix2by2 matrix12(1,1,1,0);
     matrix12.m00 = matrix1.m00 * matrix2.m00 + matrix1.m01 * matrix2.m10;
     matrix12.m01 = matrix1.m00 * matrix2.m01 + matrix1.m01 * matrix2.m11;
     matrix12.m10 = matrix1.m10 * matrix2.m00 + matrix1.m11 * matrix2.m10;
     matrix12.m11 = matrix1.m10 * matrix2.m01 + matrix1.m11 * matrix2.m11;
     return matrix12;
 }
 
 
 //定义2×2矩阵的幂运算
Matrix2by2 MatrixPower(unsigned int n) {
     Matrix2by2 matrix(1,1,1,0);
     if(n == 1) {
         matrix = Matrix2by2(1,1,1,0);
     }
     else if(n % 2 == 0) {
         matrix = MatrixPower(n / 2);
         matrix = MatrixMultiply(matrix, matrix);
     }
     else if(n % 2 == 1) {
         matrix = MatrixPower((n-1) / 2);
         matrix = MatrixMultiply(matrix, matrix);
         matrix = MatrixMultiply(matrix, Matrix2by2(1,1,1,0));
     }
     return matrix;
 }
 //计算Fibnacci的第n项
long Fibonacci(unsigned int n) {
     if(n == 0)
         return 0;
     if(n == 1)
         return 1;
 
     Matrix2by2 fibMatrix = MatrixPower(n-1);
     return fibMatrix.m00;     
 }
 
 int main() {
     cout << "Enter A Number:" << endl;
     unsigned int number;
     cin >> number;
     cout << Fibonacci(number) << endl;
     return 0;
 }

（整理自网络）

参考资料：

https://blog.csdn.net/qq_41035588/article/details/81814547