深度学习之解密Batch Normalization
本文主要是对知乎、CSDN平台上BN相关文章的转载、整理与汇总,记录以方便自己日后的复习巩固,并分享给同样渴望知识的你们。
主体来自知乎soplars理解Batch Normalization系列文章,感谢作者的耕耘!
一图解释BN作用:

简单粗暴地说,BN就是按批次对网络输出的数据分布先进行一个标准化,再进行一个“还原化”。(归一化 、标准化 和中心化/零均值化)

原理
初始idea
如果做神经网络训练前,对输入的像素进行标准化处理,将有效降低模型的训练难度(见神经网络训练技巧的初始化部分)。受此启发,作者想到,既然输入层可以加标准化有好处,那么网络里的隐层为什么不可以标准化?
于是,作者通过对每层加权和进行标准化,然后再通过缩放平移来“适度还原”。这样,做到了既不过分破坏输入信息,又抑制了各batch之间各位置点像素分布的剧烈变化带来的学习难度。
在原作中,最主要的思想就是下面这个公式。

原始神经网络的结构
一个经典的神经网络,它的某一个隐层如下图所示:
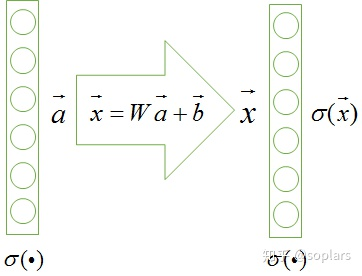
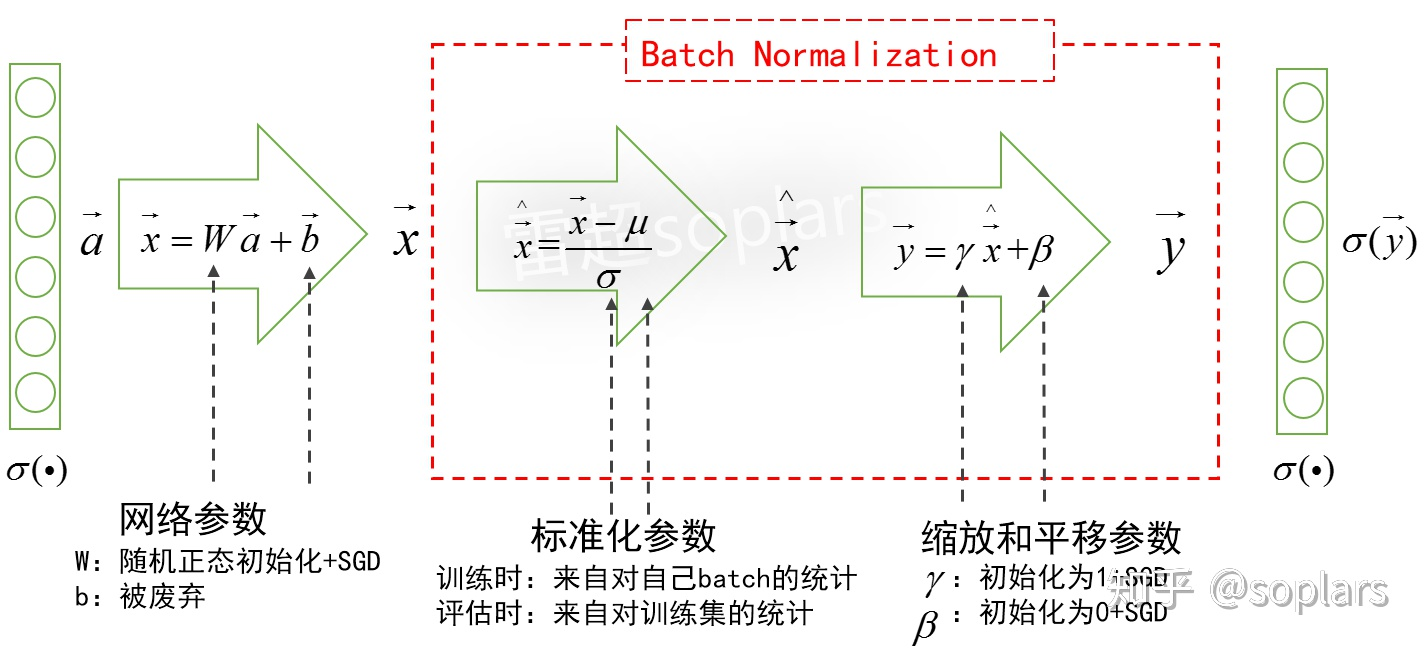
为了和原始论文统一,将之前常见的加权和符号$\vec z$改用$\vec x$表示。即上一层输出的激活值为$\vec a$ ,那么经过本层加权和$W\vec a + \vec b$处理后,获得加权和$\vec x$,然后经过本层激活后即输出$\sigma(\vec x)$。
BN的神经网络结构
加入BN之后的网络结构如图所示。
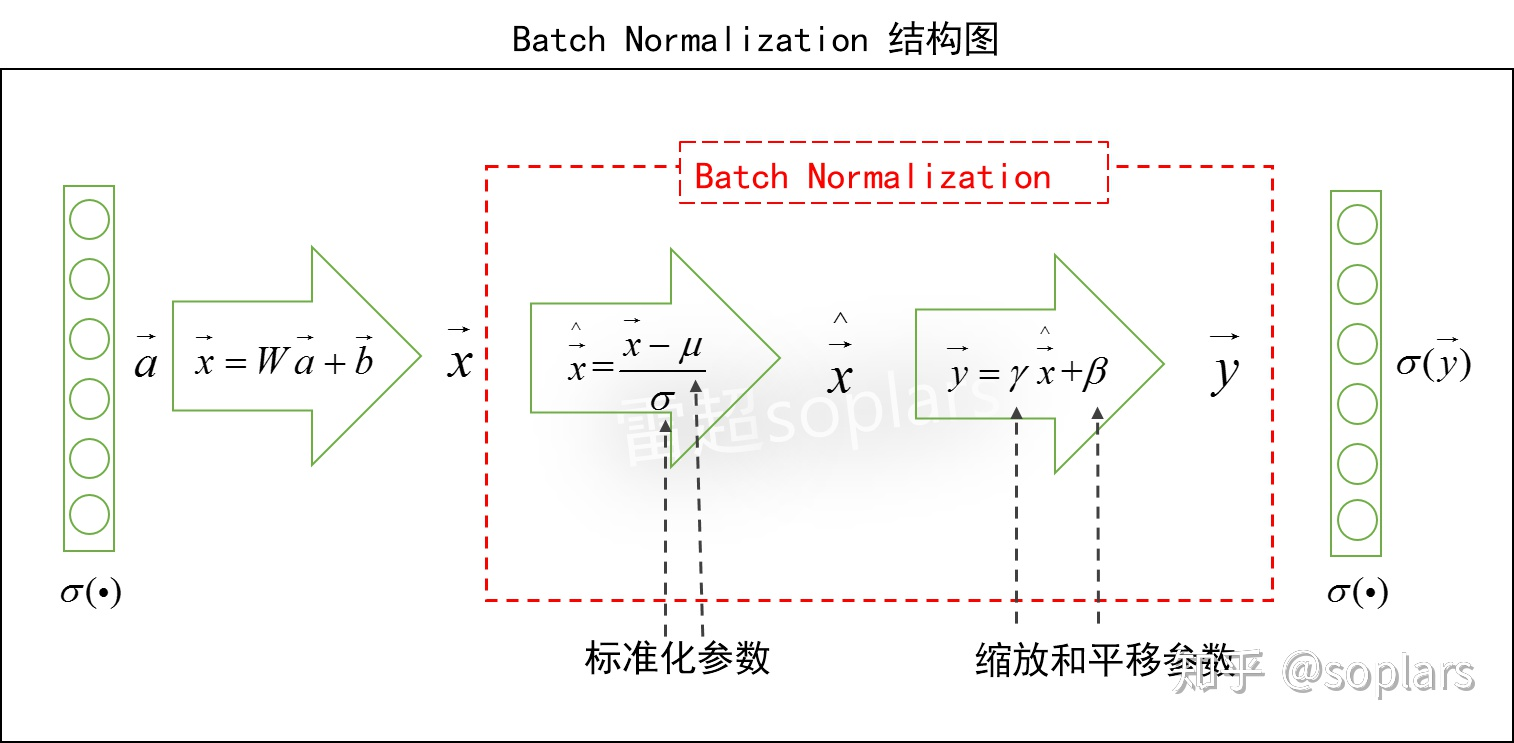
总体上来说,对于本层的加权和$\vec x$,
- BN先进行标准化求出$\hat{\vec x}$;
- 再进行缩放和平移求出$\vec y$,这个$\vec y$取代了原始的$\vec x$,然后进行激活。
BN的前向传播
认识BN的困难在于维度太多了!大脑里至少能联想到三个维度:batch_size维度(时间顺序维度)、网络层维度(结构横向维度)、向量维度(结构纵向维度)。
下图用一个究极简明的例子,说明了BN到底在干啥。
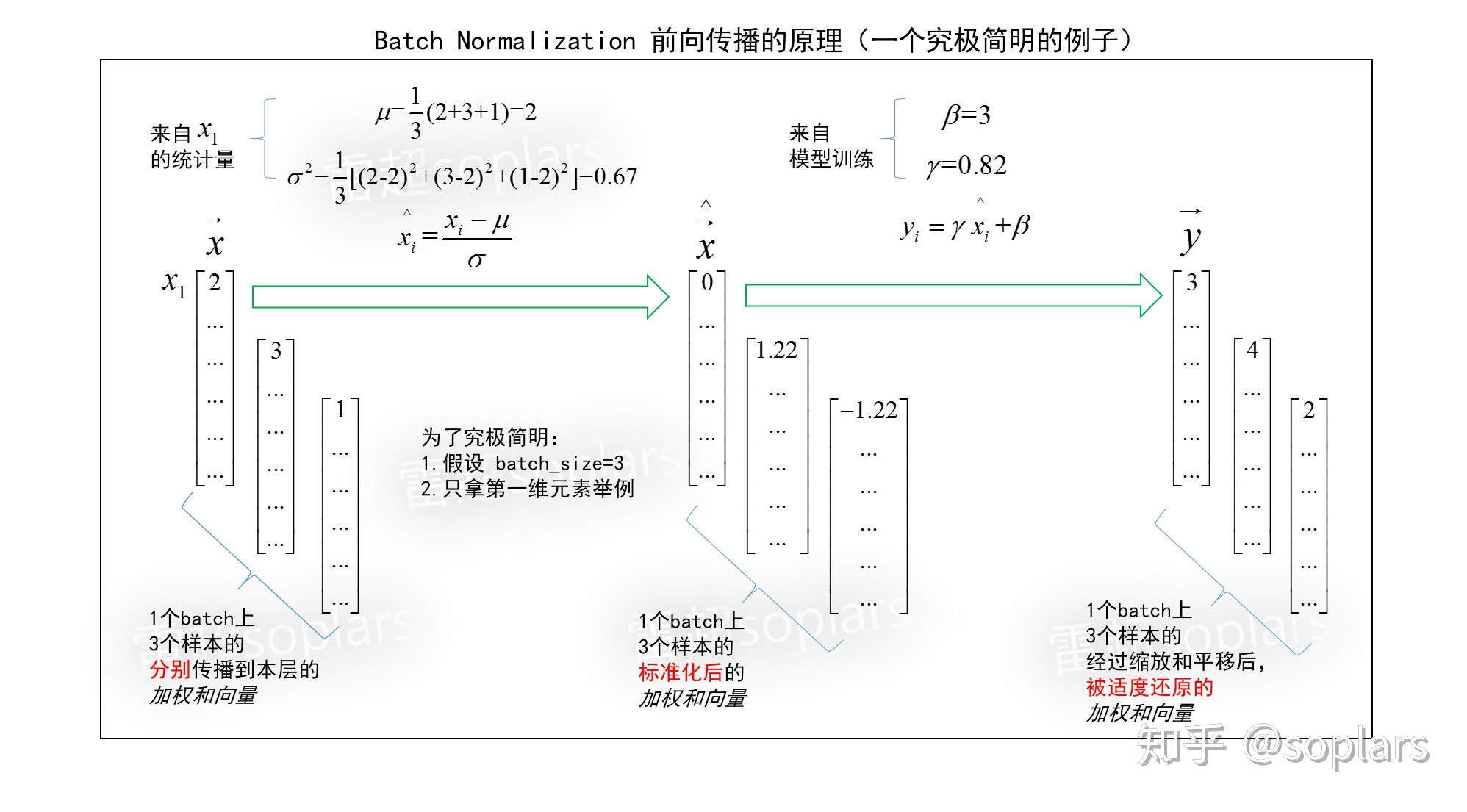
标准化
标准化即对一组数据中的每个数字,减均值再除以标准差,就可把一个该组数据转换为一个均值为$0$方差为$1$的标准正态分布。
Batch Normalization的数据组的构造方法:一个batch上所有m个样本分别进行前向传播时,传到这个隐层时所有m个$\vec x$的每个维度,分别构成一个数据组。
在原始论文里,用下标B指的正是一个batch(也就是我们常说的mini-batch),包含m个样本。这也就是为啥叫Batch Normalization的原因。
- 对这m个$\vec x$,每一个维度上的标量们,分别求均值和方差。
- 得到的均值$\mu$和方差$\sigma^2$分别对应该层的每个神经元维度。
只要我们求得均值$\mu$和方差$\sigma^2$,就可以进行标准化了:$\hat{x_i} = \frac{x_i - \mu}{\sqrt{\sigma^2}}$
为避免分母为$0$的极端情况,工程上可以给分母增加一个非常小的小数$\epsilon$(例如$10^{-8}$):$\hat{x_i} = \frac{x_i - \mu}{\sigma^2 + \epsilon}$
缩放平移
由标准化公式可以反推出:$x_i = \sigma \hat{x_i} + \mu$,仿照这个公式,作者构造了scale and shift公式:$y_i = \gamma\hat{x_i} + \beta$。
很直觉就能看出来,$\gamma$是对$\hat{x_i}$的缩放,\beta是对$\gamma\hat{x_i}$的平移。可以增加可学习的参数$\gamma, beta$,如果$\gamma = \sigma, \beta = \mu$,那么必然有$y_i = x_i$,即我们就能够完全地还原成功!
我们可以通过反向传播来训练这两个参数(推导表明这是可以训练的),而至于$\gamma$多大程度上接近$\sigma$,$\beta$多大程度上接近$\mu$,让损失函数对它们计算出的梯度决定!注意,$\gamma$ 和 $\beta$都是向量。
因此,
- 只要损失函数有需要,scale and shift公式赋予了它左右BN层还原程度的能力,而且上限是完全还原;
- 具体对每一层还原多少,则是由损失函数对每一层这两个系数的梯度来决定;
- 损失通过梯度来控制还原的程度,较好利于减少损失,就多还原;较少利于减少损失,就少还原。
BN实现的效果
又回到了这张图:
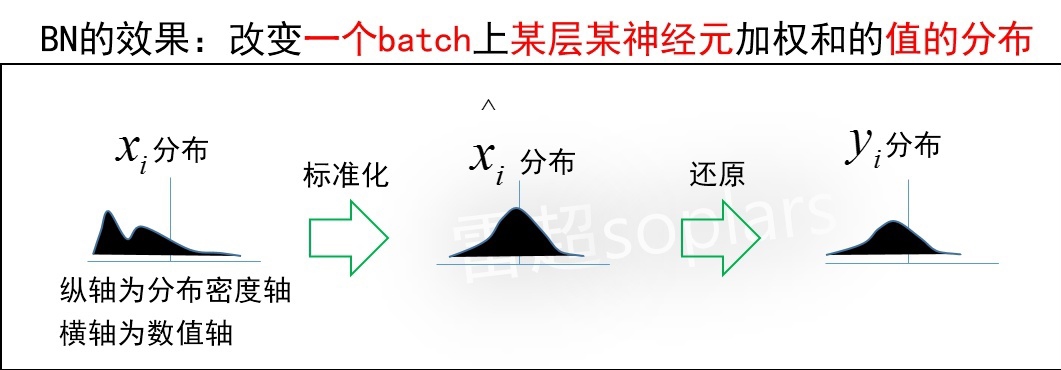
BN实现的效果是:对于某一层$\vec x$来说,它的每个元素$x_i$的数值,在一个batch上的分布是一个任意的未知分布,BN首先把它标准化为了一个标准正态分布。
这样是否太暴力了?如果所有输入样本被层层改分布,相当于输入信息都损失掉了,网络是没法训练的。所以需要第二步对标准正态分布再进行一定程度的还原操作,即缩放平移。
最终使得这个数值分布,兼顾保留有效信息、加速梯度训练。
训练及评估
训练阶段
引入BN,增加了$\mu, \sigma, \gamma, \beta$四个参数。
这四个参数的引入,能否计算梯度?它们分别是如何初始化与更新的?
反向传播
神经网络的训练,离不开反向传播,必须保证BN引入的两个操作(标准化、缩放平移)均可导。
缩放平移就是一个线性公式,求导很简单。而对于标准化时的统计量,可以绘制计算图,如下图所示。Frederik Kratzert 在这篇博文中有详细的计算,对每一个环节都进行了详细的描述。
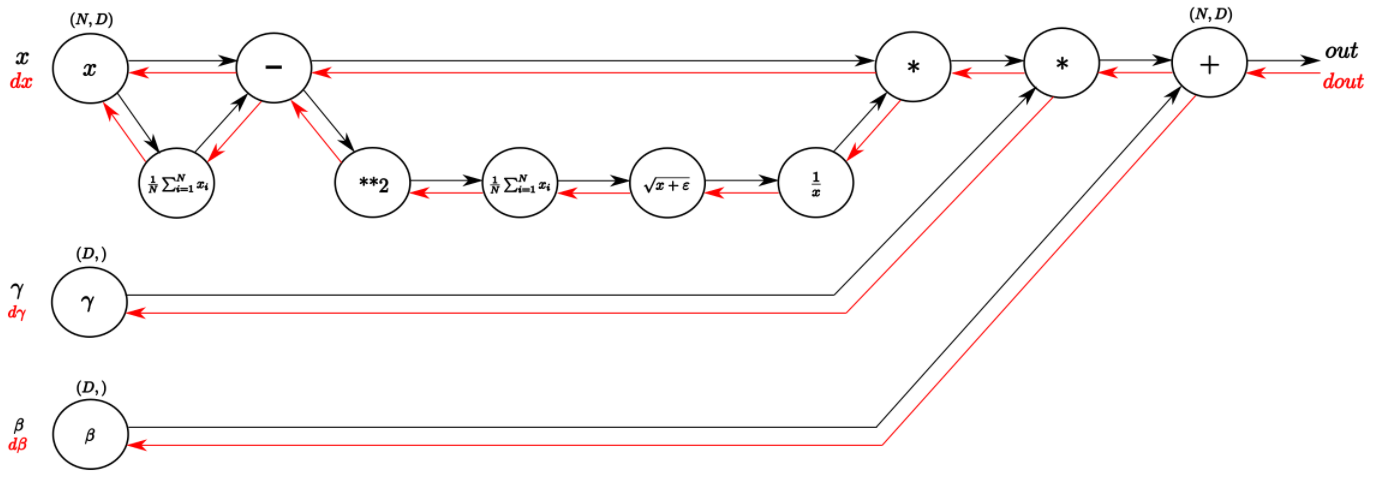
上图可见:
- 每个环节都可导
- 只要求出各个环节的导数
- 用链式法则(串联关系就相乘,并联关系就相加)求出总梯度。
狗尾续貂,对这个反传大致做了一个流程图,如下图所示,帮助理解。
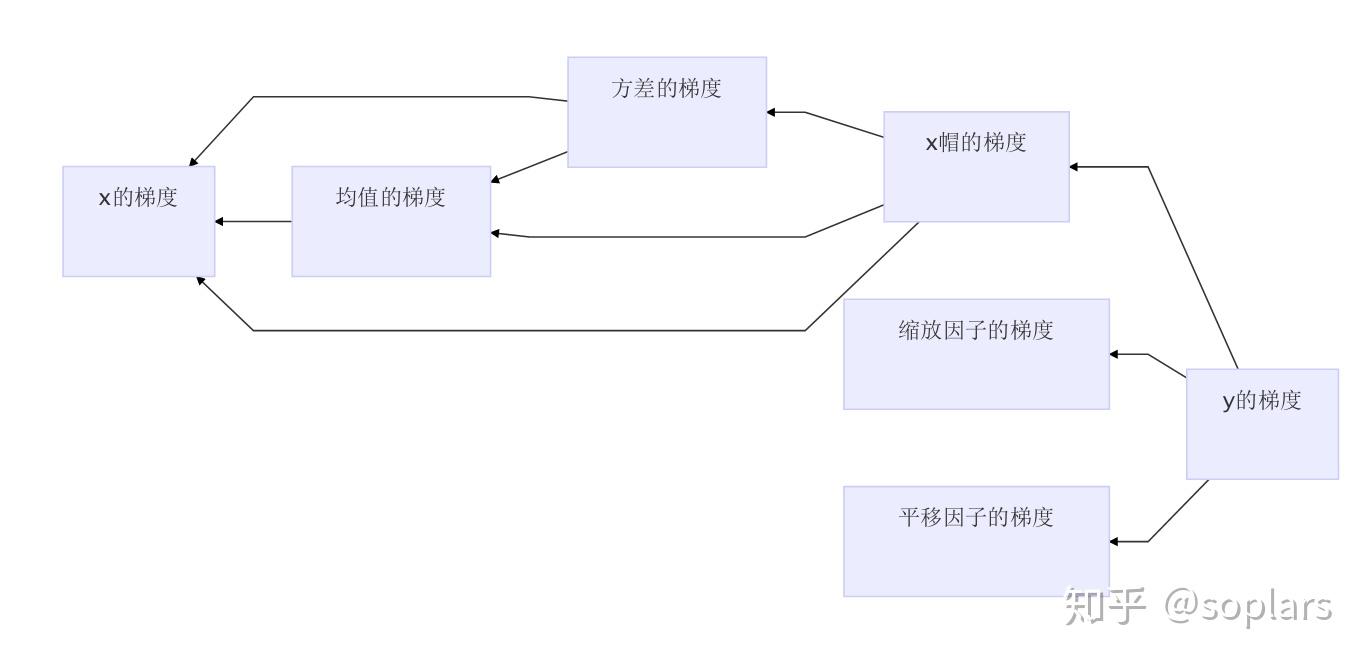
注意,均值的梯度、方差的梯度的计算,只是为了保证梯度的反向传播链路的通畅,而不是为了更新自己(没明白下文还会解释);缩放因子$\gamma$和平移因子$\beta$的梯度传播则和权重$W$一样,不影响反向传播链路的通畅,只是为了更新自己。
最后的结果就是原论文中表述:

参数的初始化及更新
讨论一下参数的初始化及更新问题。
- $W$
初始化用标准正态分布,更新用梯度下降。
与经典网络的初始化相同,初始化一个标准正态分布(即Xavier方法)。 - $b$
省略掉该参数。
在经典的神经网络里,$b$作为偏置,用于解决那些$W$无法通过与$x$相乘搞定的"损失减少要求",即对于本层所有神经元的加权和进行各自的平移。而加入BN后,$\beta$的作用正是进行平移。$b$的作用被$\beta$所完全替代了,因此省略掉$b$。
了解过ResNet结构的朋友会发现该网络中的卷积,都没有偏置,为什么?下面截图是Kaiming He在github上回答原话。(踩坑无数必须体会深刻)

- $\mu$和$\sigma$
初始化取决于统计量,仅更新梯度,但不更新值本身。
在训练阶段,每个mini-batch上进行前向传播时,通过对本batch上的$m$个样本进行统计得到;
在反向传播时,计算出它们的梯度$\ell$对$\mu$的梯度、$\ell$对$\sigma$的梯度,用于进行梯度传播。
但是$\mu$和$\sigma$这两个值本身不必进行更新,因为在下一个mini-batch会计算自己的统计量,所以前一个mini-batch获得的$\mu$和$\sigma$没意义。$\gamma$和$\beta$ - 初始化为1、0,更新用梯度下降。
$\gamma$作为“准方差”,初始化为一个全1向量;而$\beta$作为"准均值”,初始化为一个全$0$向量,他俩的初始值对于刚刚完成标准正态化的$\hat{\vec x}$来说,没起任何作用。
至于将要变成什么值,起多大作用,那就交给后续的训练,即采用梯度下降进行更新,方式同$W$。
评估阶段
$\gamma, \beta$是在整个训练集上训练出来的,与$W$一样,训练结束就可获得。
然而,$\mu$和$\sigma$是靠每一个mini-batch的统计得到,因为评估时只有一条样本,batch_size相当于是1,在只有1个向量的数据组上进行标准化后,成了一个全0向量,这可咋办?
来自训练集的均值和方差
做法是用训练集来估计总体均值$\mu$和总体标准差$\sigma$。
- 简单平均法
把每个mini-batch的均值和方差都保存下来,然后训练完了求均值的均值,方差的均值即可。 - 移动指数平均(Exponential Moving Average)
这是对均值的近似。
仅以$\mu$举例:$\mu_{total} = decay * \mu_{total} + (1 - decay) * \mu$,其中$decay$是衰减系数。即总均值$\mu_{total}$是前一个mini-batch统计的总均值和本次mini-batch的$\mu$加权求和。至于衰减率$decay$在区间$[0, 1]$之间,$decay$越接近1,结果$\mu_{total}$越稳定,越受较远的大范围的样本影响;$decay$越接近0,结果$\mu_{total}$越波动,越受较近的小范围的样本影响。
事实上,简单平均可能更好,简单平均本质上是平均权重,但是简单平均需要保存所有BN层在所有mini-batch上的均值向量和方差向量,如果训练数据量很大,会有较可观的存储代价。移动指数平均在实际的框架中更常见(例如tensorflow),可能的好处是EMA不需要存储每一个mini-batch的值,永远只保存着三个值:总统计值、本batch的统计值,$decay$系数。
在训练阶段同步获得了$\mu_{total}$和$\sigma_{total}$后,在评估时即可对样本进行BN操作。
评估阶段的计算
为避免分母不为0,增加一个非常小的常数$\epsilon$,并为了计算优化,被转换为:
这样,只要训练结束,$\frac{\gamma}{\sqrt{\sigma^2_{total} + \epsilon}}、\mu_{total}、\beta$就已知了,1个BN层对一条测试样本的前向传播只是增加了一层线性计算而已。
一张图小结:
补充解答
BN改善了ICS吗?
原作者认为BN是旨在解决了 ICS(Internal Covariate Shift)问题。原文是这样解释:

什么是ICS?
所谓Covariate Shift,是指相比于训练集数据的特征,测试集数据的特征分布发生了变化。
而原作者定义的Internal Covariate Shift,设想把每层神经网络看做一个单独的模型,它有着自己对应的输入与输出。如果这个“模型”越靠近输出层,由于训练过程中前面多层的权重的更新频繁,导致它每个神经元的输入(即上一层的激活值)的数值分布,总在不停地变化,这导致训练困难。
【更详细通俗地讲,网络一旦train起来,那么参数就要发生更新,除了输入层的数据外(因为输入层数据,我们已经人为地为每个样本归一化),后面网络每一层的输入数据分布是一直在发生变化的。因为在训练的时候,前面层训练参数的更新将导致后面层输入数据分布的变化。以网络第二层为例:网络的第二层输入,是由第一层的参数和input计算得到的,而第一层的参数在整个训练过程中一直在变化,因此必然会引起后面每一层输入数据分布的改变。我们把网络中间层在训练过程中,数据分布的改变称之为:“Internal Covariate Shift”。
对于深度网络的训练是一个复杂的过程,只要网络的前面几层发生微小的改变,那么后面几层就会被累积放大下去。一旦网络某一层的输入数据的分布发生改变,那么这一层网络就需要去适应学习这个新的数据分布,所以如果训练过程中,训练数据的分布一直在发生变化,那么将会影响网络的训练速度。】
然而,一个启发性的解释很容易被推翻,又有人做了更进一步的解释。
BN与ICS无关
2018年的文章《How Does Batch Normalization Help Optimization?》做了实验,如下图所示。

- 应用了BN,观察到的右图(Standard + BatchNorm)的激活值分布变化很明显,理论上将引起明显的ICS问题。
- 在BN层后叠加噪音(输入到后面的非线性激活,相当于BN白干了),观察到的右图(Standard+"Noisy" BatchNorm)的激活值分布变化更为突出,理论上将引起更为明显的ICS问题。
(然而,我的理解是:如果每个BN层后叠加噪音,下一层的BN也会进行标准化,层层抵消,相当于仅最后一个BN层后叠加的噪音增大了ICS)然而两种情况下,左图BN的表现依然非常稳定。即BN并没有减少ICS。
那么,BN是为什么有效?
BN改善了损失的平滑性
上图论文的作者定义了一个描述损失函数平滑度的函数,观察加入BN的前后,损失函数平滑性的变化。如下图所示,纵轴的数值越小,表明损失函数曲面越平滑;纵轴数值越大,表明损失函数曲面越颠簸。蓝色线为加入BN后的损失函数的平滑度,可以看到,加入BN后,损失函数曲面的平滑程度得到了显著改善。
什么是平滑性?
对平滑性的理解,我想没有比下图更合适的了:
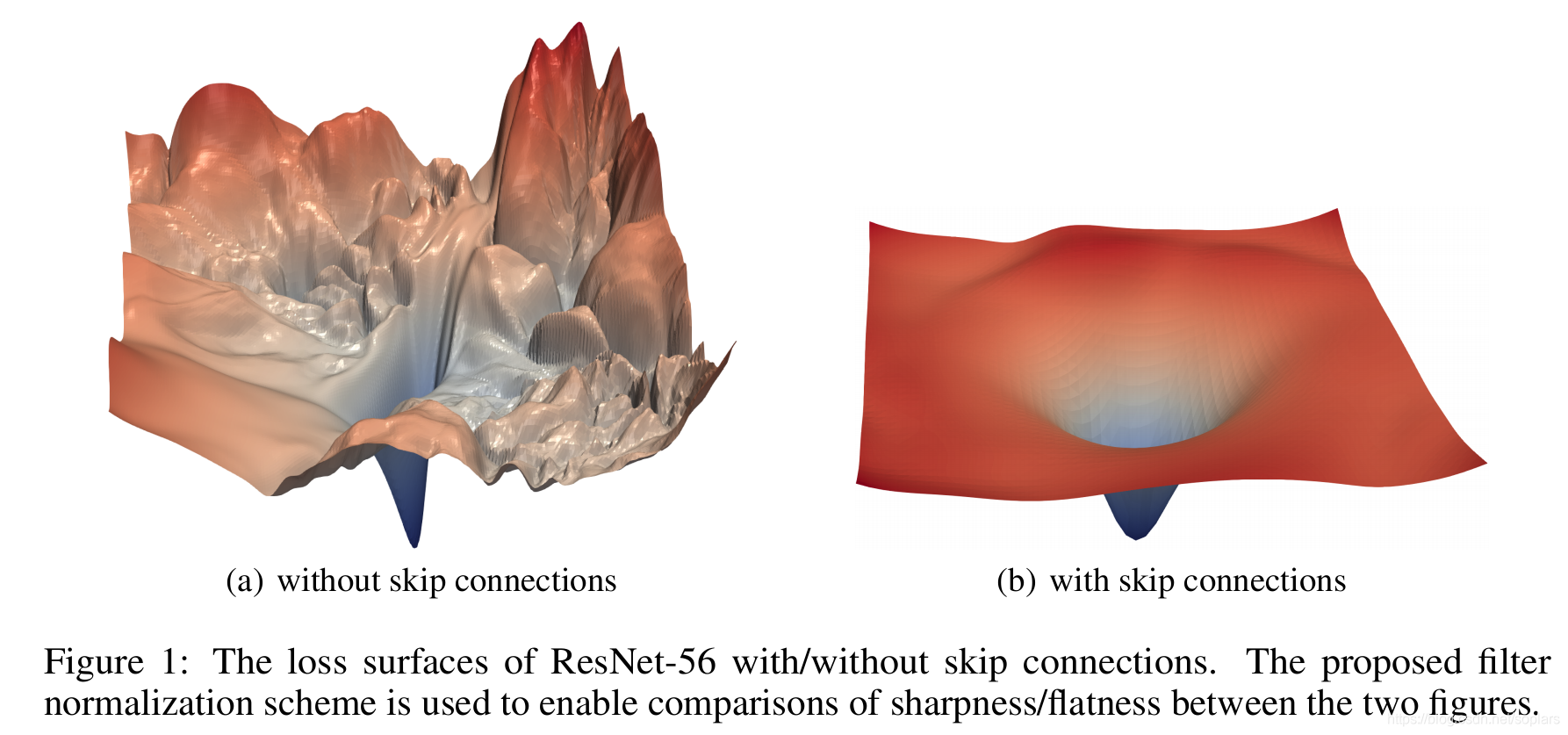
其他值得讨论的问题
BN层的位置能不能调整?如果能调整哪个位置更好?
能。原因:由前述BN的反向传播可知,BN不管放在网络的哪个位置,都可以实现这两个功能:训练$\gamma$和$\beta$、传递梯度到前一层,所以位置并不限于ReLU之前。原始论文中,BN被放在本层ReLU之前,即$$\vec a^{l+1} = ReLU[BN(W^{l+1}\vec a^l + \vec b^{l+1})]$$
也有[测试](https://github.com/ducha-aiki/caffenet-benchmark/blob/master/batchnorm.md)表明,BN放在上一层ReLU之后,效果更好,即$$\vec a^{l+1} = ReLU[W^{l+1}BN(\vec a^l) + \vec b^{l+1}]$$
在训练时为什么不直接使用整个训练集的均值/方差?
使用 BN 的目的就是为了保证每批数据的分布稳定,使用全局统计量反而违背了这个初衷。在预测时为什么不直接使用整个训练集的均值/方差?
batch_size的配置
对学习率有何影响?
BN是正则化吗?
与Dropout的有何异同?
能否和Dropout混合使用?
BN可以用在哪些层?
BN可以用在哪些类型的网络?
BN的缺点
除此之外,从上述也可以看出,batch normalization依赖于batch的大小,当batch值很小时,计算的均值和方差不稳定。研究表明对于ResNet类模型在ImageNet数据集上,batch从16降低到8时开始有非常明显的性能下降,在训练过程中计算的均值和方差不准确,而在测试的时候使用的就是训练过程中保持下来的均值和方差。这一个特性,导致batch normalization不适合以下的几种场景:
(1) batch非常小,比如训练资源有限无法应用较大的batch,也比如在线学习等使用单例进行模型参数更新的场景。
(2) RNN,因为它是一个动态的网络结构,同一个batch中训练实例有长有短,导致每一个时间步长必须维持各自的统计量,这使得BN并不能正确的使用。在rnn中,对bn进行改进也非常的困难。不过,困难并不意味着没人做,事实上现在仍然可以使用的,不过这超出了咱们初识境的学习范围。
BN的改进
针对BN依赖于batch的这个问题,BN的作者亲自现身提供了改进,即在原来的基础上增加了一个仿射变换:$$x_i' = \frac{x_i - \mu_{\beta}}{\sigma_{\beta}}\cdot r + d$$
其中参数$r, d$就是仿射变换参数,它们本身是通过如下的方式进行计算的$r = \frac{\sigma_{\beta}}{\sigma}, d = \frac{\mu_{\beta} - \mu}{\sigma}$,其中参数都是通过滑动平均的方法进行更新:$$\begin{align}\mu & := \mu + \alpha(\mu_{\beta} - \mu) \\ \sigma & := \sigma + \alpha(\sigma_{\beta} - \sigma)\end{align}$$
在实际使用的时候,先使用BN进行训练得到一个相对稳定的移动平均,网络迭代的后期再使用刚才的方法,称为Batch Renormalization,当然$r$ 和 $d$的大小必须进行限制。
Batch Normalization的变种
Normalization思想非常简单,为深层网络的训练做出了很大贡献。对于CNN,BN的操作是在各个特征维度之间单独进行,也就是说各个通道是分别进行Batch Normalization操作的。如果输出的blob大小为$(N,C,H,W)$,那么在每一层normalization就是基于$N*H*W$个数值进行求平均以及方差的操作。而因为有依赖于样本数目的缺陷,所以也被研究人员盯上进行改进。说的比较多的就是Layer Normalization与Instance Normalization,Group Normalization了。
Layer Normalization
前面说了Batch Normalization各个通道之间是独立进行计算,如果抛弃对batch的依赖,也就是每一个样本都单独进行normalization,同时各个通道都要用到,就得到了Layer Normalization。跟Batch Normalization仅针对单个神经元不同,Layer Normalization考虑了神经网络中一层的神经元。如果输出的blob大小为(N,C,H,W),那么在每一层Layer Normalization就是基于$C*H*W$个数值进行求平均以及方差的操作。
Instance Normalization
Layer Normalization把每一层的特征通道一起用于归一化,如果每一个特征层单独进行归一化呢?也就是限制在某一个特征通道内,那就是instance normalization了。如果输出的blob大小为(N,C,H,W),那么在每一层Instance Normalization就是基于$H*W$个数值进行求平均以及方差的操作。对于风格化类的图像应用,Instance Normalization通常能取得更好的结果,它的使用本来就是风格迁移应用中提出。
Group Normalization
Group Normalization是Layer Normalization和Instance Normalization 的中间体, Group Normalization将channel方向分group,然后对每个Group内做归一化,算其均值与方差。如果输出的blob大小为(N,C,H,W),将通道C分为G个组,那么Group Normalization就是基于$G*H*W$个数值进行求平均以及方差的操作。我只想说,你们真会玩,要榨干所有可能性。
在Batch Normalization之外,有人提出了通用版本Generalized Batch Normalization,有人提出了硬件更加友好的L1-Norm Batch Normalization等,不再一一讲述。
另一方面,以上的Batch Normalization,Layer Normalization,Instance Normalization都是将规范化应用于输入数据$x$,Weight normalization则是对权重进行规范化,感兴趣的可以自行了解,使用比较少,也不在我们的讨论范围。
这么多的Normalization怎么使用呢?有一些基本的建议吧,不一定是正确答案。
(1)正常的处理图片的CNN模型都应该使用Batch Normalization。只要保证batch size较大(不低于32),并且打乱了输入样本的顺序。如果batch太小,则优先用Group Normalization替代。
(2)对于RNN等时序模型,有时候同一个batch内部的训练实例长度不一(不同长度的句子),则不同的时态下需要保存不同的统计量,无法正确使用BN层,只能使用Layer Normalization。
(3)对于图像生成以及风格迁移类应用,使用Instance Normalization更加合适。
BN的优点总结
(1) 主流观点,Batch Normalization调整了数据的分布,不考虑激活函数,它让每一层的输出归一化到了均值为0方差为1的分布,这保证了梯度的有效性,目前大部分资料都这样解释,比如BN的原始论文认为的缓解了Internal Covariate Shift(ICS)问题。
(2) 可以使用更大的学习率,Bjorck论文《Understanding batch normalization》指出BN有效是因为用上BN层之后可以使用更大的学习率,从而跳出不好的局部极值,增强泛化能力,在它们的研究中做了大量的实验来验证。
(3) 损失平面平滑。Santurkar论文《How does batch normalization help optimization?》的研究提出,BN有效的根本原因不在于调整了分布,因为即使是在BN层后模拟ICS,也仍然可以取得好的结果。它们指出,BN有效的根本原因是平滑了损失平面。之前我们说过,Z-score标准化对于包括孤立点的分布可以进行更平滑的调整。
实践
【感谢作者的代码分享与详细讲解!】
构造网络
构建两个全连接神经网络:
- 一个是普通网络,包括2个隐层,1个输出层。
- 一个是有BN的网络,包括2个隐层,1个输出层。
第1层中的BN是我们自定义的,第2层和第3层中的BN是调用tensorflow实现。
定义输入占位符,定义三个层的权重,方便后面使用
w1_initial = np.random.normal(size=(784,100)).astype(np.float32) w2_initial = np.random.normal(size=(100,100)).astype(np.float32) w3_initial = np.random.normal(size=(100,10)).astype(np.float32) # 为BN层准备一个非常小的数字,防止出现分母为0的极端情况。 epsilon = 1e-3 x = tf.placeholder(tf.float32, shape=[None, 784]) y_ = tf.placeholder(tf.float32, shape=[None, 10])
Layer 1 层:无BN
w1 = tf.Variable(w1_initial) b1 = tf.Variable(tf.zeros([100])) z1 = tf.matmul(x,w1)+b1 l1 = tf.nn.sigmoid(z1)
Layer 1 层:有BN(自定义BN层)
w1_BN = tf.Variable(w1_initial) # 因为BN的引入,b的作用被BN层替代,省略。 z1_BN = tf.matmul(x,w1_BN) # 计算加权和的均值和方差,0是指batch这个维度 batch_mean1, batch_var1 = tf.nn.moments(z1_BN,[0]) # 正则化 z1_hat = (z1_BN - batch_mean1) / tf.sqrt(batch_var1 + epsilon) # 新建两个变量scale and beta scale1 = tf.Variable(tf.ones([100])) beta1 = tf.Variable(tf.zeros([100])) # 计算被还原的BN1,即BN文章里的y BN1 = scale1 * z1_hat + beta1 # l1_BN = tf.nn.sigmoid(BN1) l1_BN = tf.nn.relu(BN1)
Layer 2 层:无BN
w2 = tf.Variable(w2_initial) b2 = tf.Variable(tf.zeros([100])) z2 = tf.matmul(l1,w2)+b2 # l2 = tf.nn.sigmoid(z2) l2 = tf.nn.relu(z2)
Layer 2 层:有BN(使用tensorflow创建BN层)
w2_BN = tf.Variable(w2_initial) z2_BN = tf.matmul(l1_BN,w2_BN) # 计算加权和的均值和方差,0是指batch这个维度 batch_mean2, batch_var2 = tf.nn.moments(z2_BN,[0]) # 新建两个变量scale and beta scale2 = tf.Variable(tf.ones([100])) beta2 = tf.Variable(tf.zeros([100])) # 计算被还原的BN2,即BN文章里的y。使用 BN2 = tf.nn.batch_normalization(z2_BN,batch_mean2,batch_var2,beta2,scale2,epsilon) # l2_BN = tf.nn.sigmoid(BN2) l2_BN = tf.nn.relu(BN2)
Layer 3 层:无BN
w3 = tf.Variable(w3_initial) b3 = tf.Variable(tf.zeros([10])) y = tf.nn.softmax(tf.matmul(l2,w3)+b3)
Layer 3 层:有BN(使用tensorflow创建BN层)
# w3_BN = tf.Variable(w3_initial) # b3_BN = tf.Variable(tf.zeros([10])) # y_BN = tf.nn.softmax(tf.matmul(l2_BN,w3_BN)+b3_BN) w3_BN = tf.Variable(w3_initial) z3_BN = tf.matmul(l2_BN,w3_BN) batch_mean3, batch_var3 = tf.nn.moments(z3_BN,[0]) scale3 = tf.Variable(tf.ones([10])) beta3 = tf.Variable(tf.zeros([10])) BN3 = tf.nn.batch_normalization(z3_BN,batch_mean3,batch_var3,beta3,scale3,epsilon) # print(BN3.get_shape()) y_BN = tf.nn.softmax(BN3)
针对普通网络和BN网络,分别定义损失、优化器、精度三个op。
- 损失使用交叉熵,因为我们输出层的激活函数为softmax。
- 优化器用梯度下降
# 普通网络的损失 cross_entropy = -tf.reduce_sum(y_*tf.log(y)) # BN网络的损失 cross_entropy_BN = -tf.reduce_sum(y_*tf.log(y_BN)) # 普通网络的优化器 train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy) # BN网络的优化器 train_step_BN = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy_BN) # 普通网络的accuracy correct_prediction = tf.equal(tf.arg_max(y,1),tf.arg_max(y_,1)) accuracy = tf.reduce_mean(tf.cast(correct_prediction,tf.float32)) # BN网络的accuracy_BN correct_prediction_BN = tf.equal(tf.arg_max(y_BN,1),tf.arg_max(y_,1)) accuracy_BN = tf.reduce_mean(tf.cast(correct_prediction_BN,tf.float32)) WARNING:tensorflow:From <ipython-input-9-175577f60212>:12: arg_max (from tensorflow.python.ops.gen_math_ops) is deprecated and will be removed in a future version. Instructions for updating: Use `argmax` instead
训练网络
- 训练普通网络、有BN网络,
- 对比训练阶段的学习曲线。
- 对比BN对输入加权和的影响。
首先是训练普通网络、有BN网络
# zs存放普通网络第2个隐层的非线性激活前的加权和向量。 # BNs存放BN网络第2个隐层的非线性激活前的加权和向量(经过了BN)。 # acc, acc_BN存放训练阶段,通过测试集测得的精度序列。用于绘制learning curve zs, BNs, acc, acc_BN = [], [], [], [] # 开一个sess,同时跑train_step、train_step_BN sess = tf.InteractiveSession() sess.run(tf.global_variables_initializer()) for i in tqdm.tqdm(range(40000)): batch = mnist.train.next_batch(60) # 运行train_step,训练无BN网络 train_step.run(feed_dict={x: batch[0], y_: batch[1]}) # 运行train_step_BN,训练有BN的网络 train_step_BN.run(feed_dict={x: batch[0], y_: batch[1]}) if i % 50 is 0: # 每50个batch,测一测精度,并把第二层的加权输入,没进BN层之前的z2,被BN层处理过的BN2,都算一遍 res = sess.run([accuracy,accuracy_BN,z2,BN2],feed_dict={x: mnist.test.images, y_: mnist.test.labels}) # 保存训练阶段的精度记录,acc是无BN网络的记录,acc_BN是有BN网络的记录, acc.append(res[0]) acc_BN.append(res[1]) # 保存训练阶段的z2,BN2的历史记录 zs.append(np.mean(res[2],axis=0)) BNs.append(np.mean(res[3],axis=0)) zs, BNs, acc, acc_BN = np.array(zs), np.array(BNs), np.array(acc), np.array(acc_BN) 100%|████████████████████████████████████| 40000/40000 [06:54<00:00, 96.44it/s]
对学习曲线的影响
对比训练阶段的学习曲线:
绘制精度训练曲线的结果表明BN的加入,大大提升了训练效率。
fig, ax = plt.subplots() ax.plot(range(0,len(acc)*50,50),acc, label='Without BN') ax.plot(range(0,len(acc)*50,50),acc_BN, label='With BN') ax.set_xlabel('Training steps') ax.set_ylabel('Accuracy') # ax.set_ylim([0.8,1]) ax.set_title('Batch Normalization Accuracy') ax.legend(loc=4) plt.show()

对加权和的影响
zs 来自无BN网络的第二个隐层的输入加权和向量,即下一步将喂给本层的激活函数。
BNs 来自有BN网络的第二个隐层的输入加权和经过BN层处理后的向量,即下一步也将喂给本层的激活函数。
- 效果:没有BN,则网络的加权和完全跑飞了;有BN,则加权和会被约束在0附近。
# 显示在无BN和有BN两个网络里,800次前向传播中第2个隐层的5个神经元的加权和的输入范围。 fig, axes = plt.subplots(5, 2, figsize=(6,12)) # fig, axes = plt.subplots(5, 2) fig.tight_layout() for i, ax in enumerate(axes): ax[0].set_title("Without BN") ax[1].set_title("With BN") # [:,i]表示取其中一列,也就是对应神经网络中 # print(zs[:,i].shape) ax[0].plot(zs[:,i]) ax[1].plot(BNs[:,i]) plt.show()

测试阶段的问题
因为测试阶段每个样本如果是逐个输入,相当于batch_size=1,那么均值为自己,方差为0,正则化后将为0。
导致模型的输入永远是一个0值。因此预测将根据训练的权重输出一个大概率是错误的预测。
predictions = [] correct = 0 for i in range(100): pred, corr = sess.run([tf.arg_max(y_BN,1), accuracy_BN], feed_dict={x: [mnist.test.images[i]], y_: [mnist.test.labels[i]]}) # 累加,最终用于求取100次预测的平均精度 correct += corr # 保存每次预测的结果 predictions.append(pred[0]) print("PREDICTIONS:", predictions) print("ACCURACY:", correct/100) sess.close() # 结果将是:不管输入的是什么照片,结果都将相同。因为每个图片在仅有自己的mini-batch上都被标准化为了全0向量。 PREDICTIONS: [8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8] ACCURACY: 0.02
实际应用的细节
为了避免推理(or预测)时出现的问题,需要注意一下几点:
构造BN层
batch_norm_wrapper将实现在更为高级的功能,合二为一:
- 训练阶段,统计训练集均值和方差;
- 推理阶段,直接使用训练阶段的统计结果。
# batch_norm_wrapper 是对tensorflow中BN层实现的一个核心功能的重现。 # https://github.com/tensorflow/tensorflow/blob/master/tensorflow/contrib/layers/python/layers/layers.py#L102 # 其功能是:对于每个batch的每一层的加权输入 # 在训练阶段,统计方差和均值,一边记录和更新总体方差和均值。 # 在测试/评估阶段,直接使用训练时统计好的总体方差和均值。 def batch_norm_wrapper(inputs, is_training, decay = 0.999): # 每个BN层,引入了4个变量 scale beta pop_mean pop_var,其中: # scale beta 是可训练的,训练结束后被保存为模型参数 # pop_mean pop_var 是不可训练,只在训练中进行统计, # pop_mean pop_var 最终保存为模型的变量。在测试时重构的计算图会接入该变量,只要载入训练参数即可。 scale = tf.Variable(tf.ones([inputs.get_shape()[-1]])) beta = tf.Variable(tf.zeros([inputs.get_shape()[-1]])) pop_mean = tf.Variable(tf.zeros([inputs.get_shape()[-1]]), trainable=False) pop_var = tf.Variable(tf.ones([inputs.get_shape()[-1]]), trainable=False) if is_training: # 以下为训练时的BN计算图构造 # batch_mean、batch_var在一个batch里的每一层,在前向传播时会计算一次, # 在反传时通过它来计算本层输入加权和的梯度,仅仅作为整个网络传递梯度的功能。在训练结束后被废弃。 batch_mean, batch_var = tf.nn.moments(inputs,[0]) # 通过移动指数平均的方式,把每一个batch的统计量汇总进来,更新总体统计量的估计值pop_mean、pop_var # assign构建计算图一个operation,即把pop_mean * decay + batch_mean * (1 - decay) 赋值给pop_mean train_mean = tf.assign(pop_mean,pop_mean * decay + batch_mean * (1 - decay)) train_var = tf.assign(pop_var,pop_var * decay + batch_var * (1 - decay)) # 确保本层的train_mean、train_var这两个operation都执行了,才进行BN。 with tf.control_dependencies([train_mean, train_var]): return tf.nn.batch_normalization(inputs,batch_mean, batch_var, beta, scale, epsilon) else: # 以下为测试时的BN计算图构造,即直接载入已训练模型的beta, scale,已训练模型中保存的pop_mean, pop_var return tf.nn.batch_normalization(inputs,pop_mean, pop_var, beta, scale, epsilon)
构造计算图
def build_graph(is_training): x = tf.placeholder(tf.float32, shape=[None, 784],name="x") y_ = tf.placeholder(tf.float32, shape=[None, 10],name="y_") w1 = tf.Variable(w1_initial) z1 = tf.matmul(x,w1) bn1 = batch_norm_wrapper(z1, is_training) l1 = tf.nn.sigmoid(bn1) w2 = tf.Variable(w2_initial) z2 = tf.matmul(l1,w2) bn2 = batch_norm_wrapper(z2, is_training) l2 = tf.nn.sigmoid(bn2) w3 = tf.Variable(w3_initial) # b3 = tf.Variable(tf.zeros([10])) # y = tf.nn.softmax(tf.matmul(l2, w3)) z3 = tf.matmul(l2,w3) bn3 = batch_norm_wrapper(z3, is_training) y = tf.nn.softmax(bn3) cross_entropy = -tf.reduce_sum(y_*tf.log(y)) train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy) correct_prediction = tf.equal(tf.arg_max(y,1),tf.arg_max(y_,1)) accuracy = tf.reduce_mean(tf.cast(correct_prediction,tf.float32),name='accuracy') return (x, y_), train_step, accuracy, y
训练阶段
- 通过传入is_training=True,开启计算图的方差和均值统计操作。
- 训练结束后,保存模型,包含计算图和参数,实际上只有参数会被用到,因为在预测时会新建计算图。
tf.reset_default_graph() (x, y_), train_step, accuracy, _,= build_graph(is_training=True) acc = [] with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for i in tqdm.tqdm(range(10000)): batch = mnist.train.next_batch(60) train_step.run(feed_dict={x: batch[0], y_: batch[1]}) if i % 200 is 0: res = sess.run([accuracy],feed_dict={x: mnist.test.images, y_: mnist.test.labels}) acc.append(res[0]) # print('batch:',i,' accuracy:',res[0]) # 保存模型,注意该模型是不可用的。因为其计算图是训练的计算图。 saver=tf.train.Saver() # saved_model = saver.save(sess, './temp-bn-save') saver.save(sess, './bn_test/temp-bn-save') writer=tf.summary.FileWriter('./improved_graph2',sess.graph) writer.flush() writer.close() print("Final accuracy:", acc[-1]) 100%|███████████████████████████████████| 10000/10000 [00:38<00:00, 260.31it/s] Final accuracy: 0.9538
测试阶段
先构造推理的计算图,再把训练好的模型参数载入到这个计算图中。
tf.reset_default_graph() # (x, y_), _, accuracy, y, saver = build_graph(is_training=False) (x, y_), _, accuracy, y = build_graph(is_training=False) predictions = [] correct = 0 with tf.Session() as sess: sess.run(tf.global_variables_initializer()) # 读取训练时模型,将学到的权重参数、估计的总体均值、方差,通过restore,载入到运行的计算图中。 saver=tf.train.Saver() saver.restore(sess, './bn_test/temp-bn-save') saver.save(sess, './bn_release/temp-bn-save') for i in range(100): pred, corr = sess.run([tf.arg_max(y,1), accuracy], feed_dict={x: [mnist.test.images[i]], y_: [mnist.test.labels[i]]}) correct += corr predictions.append(pred[0]) print("PREDICTIONS:", predictions) print("ACCURACY:", correct/100) INFO:tensorflow:Restoring parameters from ./bn_test/temp-bn-save PREDICTIONS: [7, 2, 1, 0, 4, 1, 4, 9, 6, 9, 0, 6, 9, 0, 1, 5, 9, 7, 3, 4, 9, 6, 6, 5, 4, 0, 7, 4, 0, 1, 3, 1, 3, 4, 7, 2, 7, 1, 2, 1, 1, 7, 4, 2, 3, 5, 1, 2, 4, 4, 6, 3, 5, 5, 6, 0, 4, 1, 9, 7, 7, 8, 9, 3, 7, 4, 1, 4, 3, 0, 7, 0, 2, 9, 1, 7, 3, 2, 9, 7, 7, 6, 2, 7, 8, 4, 7, 3, 6, 1, 3, 6, 9, 3, 1, 4, 1, 7, 6, 9] ACCURACY: 0.97
其他可以做的试验
如果感兴趣,不妨基于上面的代码继续进行试验
BN到添加位置试验
在加权和后 vs 在加权和前
靠近输入层 vs 靠近输出层
BN的添加量试验
在每一层都加BN vs 在少数几层加BN
BN对学习率的影响
大学习率 vs 小学习率
Batch_size对BN效果的影响
小batch_size vs 大batch_size


 浙公网安备 33010602011771号
浙公网安备 33010602011771号