向量叉积之判断两条线段相交

数学基础：向量叉乘

详情点击数学基础之向量点乘与叉乘

判断线段相交

常用的方法是通过向量叉乘来判断，这种方法不需要算出直线方程（再判断交点有否），在代码实现上比较简便。
用这种方法判别线段是否相交一般分为两步：
    1. 快速排斥实验
    2. 跨立实验

Part1：快速排斥实验

首先判断两条线段在$x$以及$y$坐标的投影是否有重合。也就是判断一个线段中$x$较大的端点是否小于另一个线段中$x$较小的段点，若是，则说明两个线段必然没有交点，同理判断下$y$。

//如果四条判断有一个为真，则代表两线段必不可交，否则应该进行第二步判断。
max(C.x,D.x)<min(A.x,B.x) || max(C.y,D.y)<min(A.y,B.y) || max(A.x,B.x)<min(C.x,D.x) || max(A.y,B.y)<min(C.y,C.y)

显然，上图通不过快速排斥实验。

Part2：跨立实验

向量间的顺逆时针关系

计算向量叉乘是与直线和线段相关算法的核心部分。
设向量$\vec P = (x_1, y_1)$，$\vec Q = (x_2, y_2)$，则向量叉乘定义为：$\vec P \times \vec Q = x_1 * y_2 - x_2 * y_1$，其结果是一个向量，且为向量$\vec P$, $\vec Q$所在平面的法向量。显然有性质$\vec P \times \vec Q = - (\vec Q \times \vec P)$和$\vec P \times (-\vec Q) = - (\vec P \times \vec Q)$。
叉乘的一个非常重要性质是可以通过它的符号判断两向量相互之间的顺逆时针关系：

• 　　若$\vec P \times \vec Q > 0$, 则$\vec P$在$\vec Q$的顺时针方向。
• 　　若$\vec P \times \vec Q < 0$, 则$\vec P$在$\vec Q$的逆时针方向。
• 　　若$\vec P \times \vec Q = 0$, 则$\vec P$与$\vec Q$共线，但可能同向也可能反向。

通过叉乘来判断线段相交

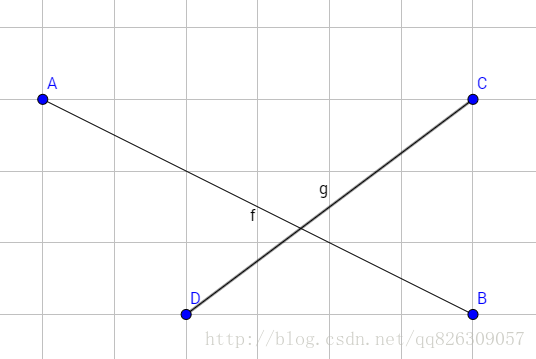
如果两线段相交那么就意味着它们互相跨立，即如上图点A和B分别在线段CD两侧，点C和D分别在线AB两侧。

判断A点与B点是否在线段DC的两侧，即向量$\vec {AD}$与向量$\vec {BD}$分别在向量$\vec {CD}$的两端，也就是其叉积是异号的，即($\vec {AD}$ $\times$ $\vec {CD}$) ∗ ($\vec {BD}$ $\times$ $\vec {CD}$) < 0。同时也要证明C点与D点在线段AB的两端，两个同时满足，则表示线段相交。

然后我们来看看临界情况，也就是上式恰好等于 0 的情况下：

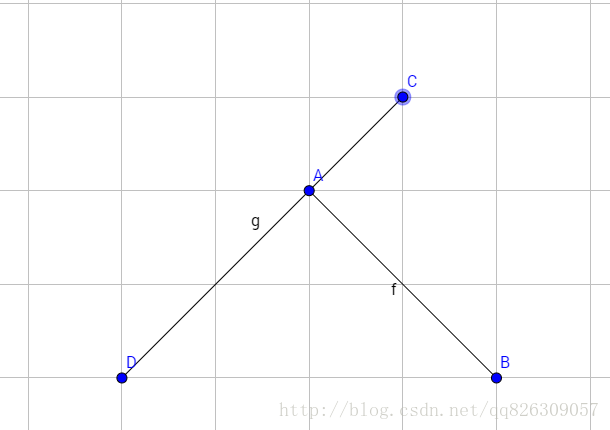
当出现如上图所示的情况的时候，($\vec {AD}$ $\times$ $\vec {CD}$) * ($\vec {BD}$ $\times$ $\vec {CD}$) = 0，显然，这种情况是相交的。只要将等号直接补上即可。

再接得想一想，如果没有第一步的快速排斥实验，仅判断第二步，会出现什么问题？

 

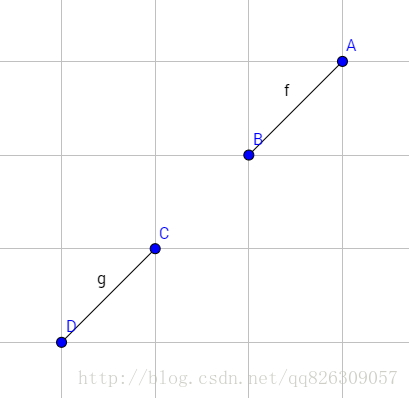
 当出现如上所示的情况的时候，叉积都为 0, 可以通过跨立实验，但是两个线段并没有交点。不过还好，这种情况在第一步快速排斥已经被排除了。

代码实现

struct Line {
    double x1;
    double y1;
    double x2;
    double y2;
};

bool intersection(const Line &l1, const Line &l2)
{
    //快速排斥实验
    if ((l1.x1 > l1.x2 ? l1.x1 : l1.x2) < (l2.x1 < l2.x2 ? l2.x1 : l2.x2) ||
        (l1.y1 > l1.y2 ? l1.y1 : l1.y2) < (l2.y1 < l2.y2 ? l2.y1 : l2.y2) ||
        (l2.x1 > l2.x2 ? l2.x1 : l2.x2) < (l1.x1 < l1.x2 ? l1.x1 : l1.x2) ||
        (l2.y1 > l2.y2 ? l2.y1 : l2.y2) < (l1.y1 < l1.y2 ? l1.y1 : l1.y2))
    {
        return false;
    }
    //跨立实验
    if ((((l1.x1 - l2.x1)*(l2.y2 - l2.y1) - (l1.y1 - l2.y1)*(l2.x2 - l2.x1))*
        ((l1.x2 - l2.x1)*(l2.y2 - l2.y1) - (l1.y2 - l2.y1)*(l2.x2 - l2.x1))) > 0 ||
        (((l2.x1 - l1.x1)*(l1.y2 - l1.y1) - (l2.y1 - l1.y1)*(l1.x2 - l1.x1))*
        ((l2.x2 - l1.x1)*(l1.y2 - l1.y1) - (l2.y2 - l1.y1)*(l1.x2 - l1.x1))) > 0)
    {
        return false;
    }
    return true;
}

参考资料：

https://blog.csdn.net/qq826309057/article/details/70942061