深度学习之参数初始化
初始化概念
初始化参数指的是在网络模型训练之前,对各个节点的权重和偏置进行初始化赋值的过程。
在深度学习中,神经网络的权重初始化方法(weight initialization)对模型的收敛速度和性能有着至关重要的影响。模型的训练,简而言之,就是对权重参数$W$的不停迭代更新,以期达到更好的性能。而随着网络深度(层数)的增加,训练中极易出现梯度消失或者梯度爆炸等问题。因此,对权重$W$的初始化显得至关重要,一个好的权重初始化虽然不能完全解决梯度消失或梯度爆炸的问题,但是对于处理这两个问题是有很大帮助的,并且十分有利于提升模型的收敛速度和性能表现。
初始化原则
一些基本的储备知识
在总结参数初始化的原则之前,先简单看一下网络模型运行的过程,参数初始化的目的是使网络模型能够更好地进行训练。现在大部分的网络训练依然采用误差的反向传播算法,误差反向传播分为正反两个过程,这里就不再赘述了,先引入几个概念。下面这幅图是一个神经网络的某一个层:

由图可知,每一个层内部的组成主要有:
输入$X/h^i$:来自原始样本$X$的输入($i = 0$)或上一层(第$i - 1层$)的输出$h^i$。
权重$W$:网络模型训练的主体对象,第$i$层的权重参数$w^i$。
状态值$z$:作为每一层激活函数$f$的输入,处于网络层的内部,所以称之为状态值。
激活值$h$:状态值$z^i$经过了激活函数$f$后的输出,也就是第$i$层的最终输出$h^i$;
数据在网络模型中流动的时候,则会有(这里默认没有偏置项$B$):$$\begin{align}z^i &= w^i \cdot h^{i - 1} \\ h^i &= f(z^i)\end{align}$$
然后在反向传播的过程中,由于是复合函数的求导,根据链式法则,会有两组导数,一个是损失函数$Cost$对$z$的导数,一个是损失函数$Cost$对$W$的导数,(详细过程这里不推导),这里再引入两个概念:
1)损失函数$Cost$关于状态$z$的梯度:即$\frac{\partial Cost}{\partial z}$
2)损失函数$Cost$关于权重参数$W$的梯度:即$\frac{\partial Cost}{\partial W}$
参数初始化的几个基本条件
什么样的初始化参数才是最好的呢?
需要牢记参数初始化的目的是为了让神经网络在训练过程中学习到有用的信息,这意味着参数梯度不应该为0。而我们知道在全连接的神经网络中,参数梯度和反向传播得到的状态梯度以及入激活值有关——激活值饱和会导致该层状态梯度信息为0,然后导致下面所有层的参数梯度为0;入激活值为0会导致对应参数梯度为0。所以如果要保证参数梯度不等于0,那么参数初始化应该使得各层激活值不会出现饱和现象且激活值不为0。我们把这两个条件总结为参数初始化条件:
- 初始化必要条件一:各层激活值不会出现饱和现象。
- 初始化必要条件二:各层激活值不为$0$。
下面从最常见的全0初始化和标准随机初始化展开来讨论。
全0初始化的可行性
在线性回归,logistics回归的时候,基本上都是把参数初始化为0,我们的模型也能够很好的工作(可初始化为0的模型见这篇文章)。然后在神经网络中,把$W$初始化为0是不可以的。这是因为如果把$W$初始化$0$,那么在前向传播过程中,每一层的神经元学到的东西都是一样的(激活值均为0),而在bp的时候,不同维度的参数会得到相同的更新,因为他们的gradient相同,称之为“对称失效”(具体可看这篇文章)。下面用一段代码来演示,当把$W$初始化为$0$:
def initialize_parameters_zeros(layers_dims): """ Arguments: layer_dims -- python array (list) containing the size of each layer. Returns: parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL": W1 -- weight matrix of shape (layers_dims[1], layers_dims[0]) b1 -- bias vector of shape (layers_dims[1], 1) ... WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1]) bL -- bias vector of shape (layers_dims[L], 1) """ parameters = {} np.random.seed(3) L = len(layers_dims) # number of layers in the network for l in range(1, L): parameters['W' + str(l)] = np.zeros((layers_dims[l], layers_dims[l - 1])) parameters['b' + str(l)] = np.zeros((layers_dims[l], 1)) return parameters

import numpy as np import matplotlib.pyplot as plt def initialize_parameters(layer_dims): """ :param layer_dims: list,每一层单元的个数(维度) :return:dictionary,存储参数w1,w2,...,wL,b1,...,bL """ np.random.seed(3) L = len(layer_dims)#the number of layers in the network parameters = {} for l in range(1,L): parameters["W" + str(l)] = np.random.randn(layer_dims[l],layer_dims[l-1])*0.01 parameters["b" + str(l)] = np.zeros((layer_dims[l],1)) return parameters def forward_propagation(): data = np.random.randn(1000, 100000) # layer_sizes = [100 - 10 * i for i in range(0,5)] layer_sizes = [1000,800,500,300,200,100,10] num_layers = len(layer_sizes) parameters = initialize_parameters(layer_sizes) A = data for l in range(1,num_layers): A_pre = A W = parameters["W" + str(l)] b = parameters["b" + str(l)] z = np.dot(W,A_pre) + b #计算z = wx + b A = np.tanh(z) #画图 plt.subplot(2,3,l) plt.hist(A.flatten(),facecolor='g') plt.xlim([-1,1]) plt.yticks([]) plt.show()
我们可以看看cost function是如何变化的:
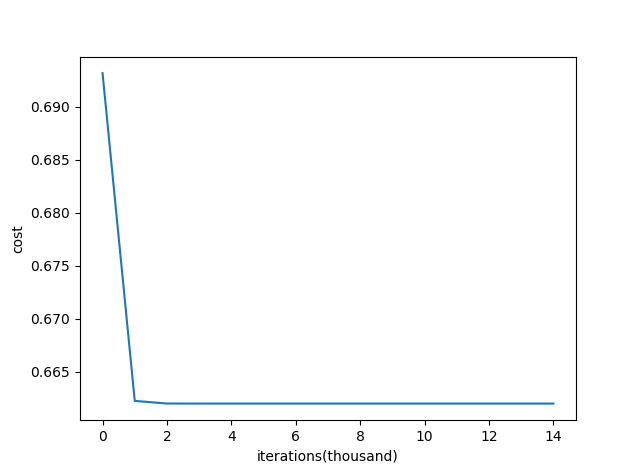
能够看到代价函数降到0.64(迭代1000次)后,再迭代已经不起什么作用了。
标准随机初始化
我们希望所有参数的期望接近$0$。遵循这个原则,可以将参数设置为接近$0$的很小的随机数(有正有负),在实际中,随机参数服从高斯分布/正态分布(Gaussian distribution / normal distribution)和均匀分布(uniform distribution)都是有效的初始化方法。还是用一段代码来演示:
def initialize_parameters_random(layers_dims): """ Arguments: layer_dims -- python array (list) containing the size of each layer. Returns: parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL": W1 -- weight matrix of shape (layers_dims[1], layers_dims[0]) b1 -- bias vector of shape (layers_dims[1], 1) ... WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1]) bL -- bias vector of shape (layers_dims[L], 1) """ np.random.seed(3) # This seed makes sure your "random" numbers will be the as ours parameters = {} L = len(layers_dims) # integer representing the number of layers for l in range(1, L): parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1])*0.01 parameters['b' + str(l)] = np.zeros((layers_dims[l], 1)) return parameters
【代码注解:
1. 是一个均值为$04,方差为$1$的高斯分布采样。
2. 乘$0.01$是因为要把$W$随机初始化到一个相对较小的值,因为如果X很大的话,$W$又相对较大,会导致$Z$非常大,这样如果激活函数是sigmoid,就会导致sigmoid的输出值$1$或者$0$,然后会导致一系列问题(比如cost function计算的时候,log里是0,这样会有点麻烦)。】
随机初始化后,cost function随着迭代次数的变化示意图为:
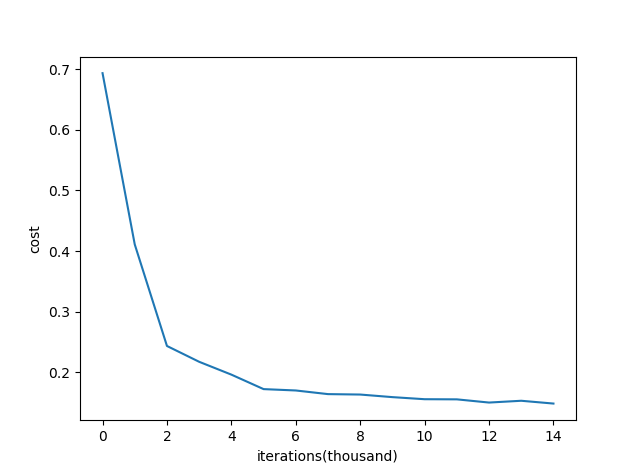
能够看出,cost function的变化是比较正常的。但是随机初始化也有缺点:当神经网络的层数增多时,会发现越往后面的层的激活函数(使用tanH)的输出值几乎都接近于0,如下图所示:
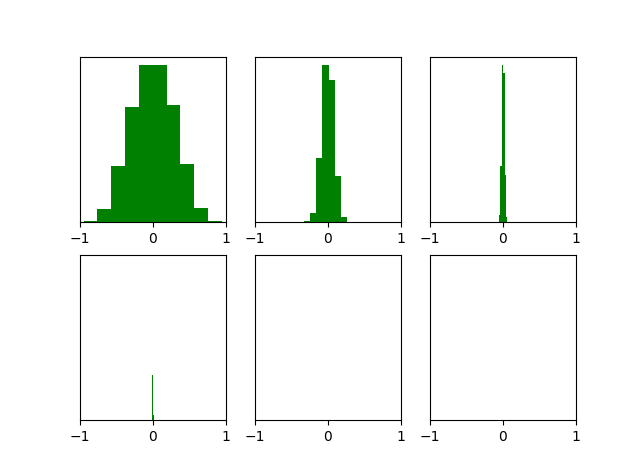
而激活函数输出值接近于0会导致梯度非常接近于$0$,因此会导致梯度消失。
总结来说,一般的随机初始化存在后层网络激活函数的输出值趋近于0的问题,且网络输出数据分布的方差会受每层神经元个数的影响(随之改变)。针对这些问题,Glorot 等人提出在初始化的同时加上对方差大小的规范化。这样不仅获得了更快的收敛速度,而且维持了输入输出数据分布方差的一致性,也避免了后面层的激活函数的输出值趋向于0的问题。
Glorot条件
这里直接引入Glorot条件——优秀的初始化应该保证以下两个条件:
(1)各个层的激活值$h$(输出值)的方差要保持一致,即$\forall(i, j) : Var(h^i) = Var(h^j)$;
(2)各个层对状态$z$的梯度的方差要保持一致,即$\forall(i, j) : Var(\frac{\partial Cost}{\partial z^i}) = Var(\frac{\partial Cost}{\partial z^i})$;
关于方差的三个事实
既然要保持上面的两个方差在各个网络层中不改变,那也就是它实际上是会改变的,关于为什么会改变的公式推导,这里不详细说明了,直接引入三个基本的客观事实(两有关一无关):
(1)各个层激活值$h$(输出值)的方差与网络的层数有关;
(2)关于状态$z$的梯度的方差与网络的层数有关;
(3)各个层权重参数$W$的梯度的方差与层数无关;
关于上面几个基本结论的详情以及公式推导,我们可以参考Xavier的原论文:Understanding the difficulty of training deep feedforward neural networks以及Vic时代的专栏深度学习之参数初始化(一)——Xavier初始化(里面有较为详实的公式推导)
借用论文中的几幅图,也可以看出这几个结论。
(1)各层激活值$h$直方图如下:
可以看出,激活值的方差逐层递减。
(2)各层状态Z的梯度的直方图如下:

状态的梯度在反向传播过程中越往下梯度越小(因为方差越来越小)。
(3)各层参数W的梯度的直方图如下:
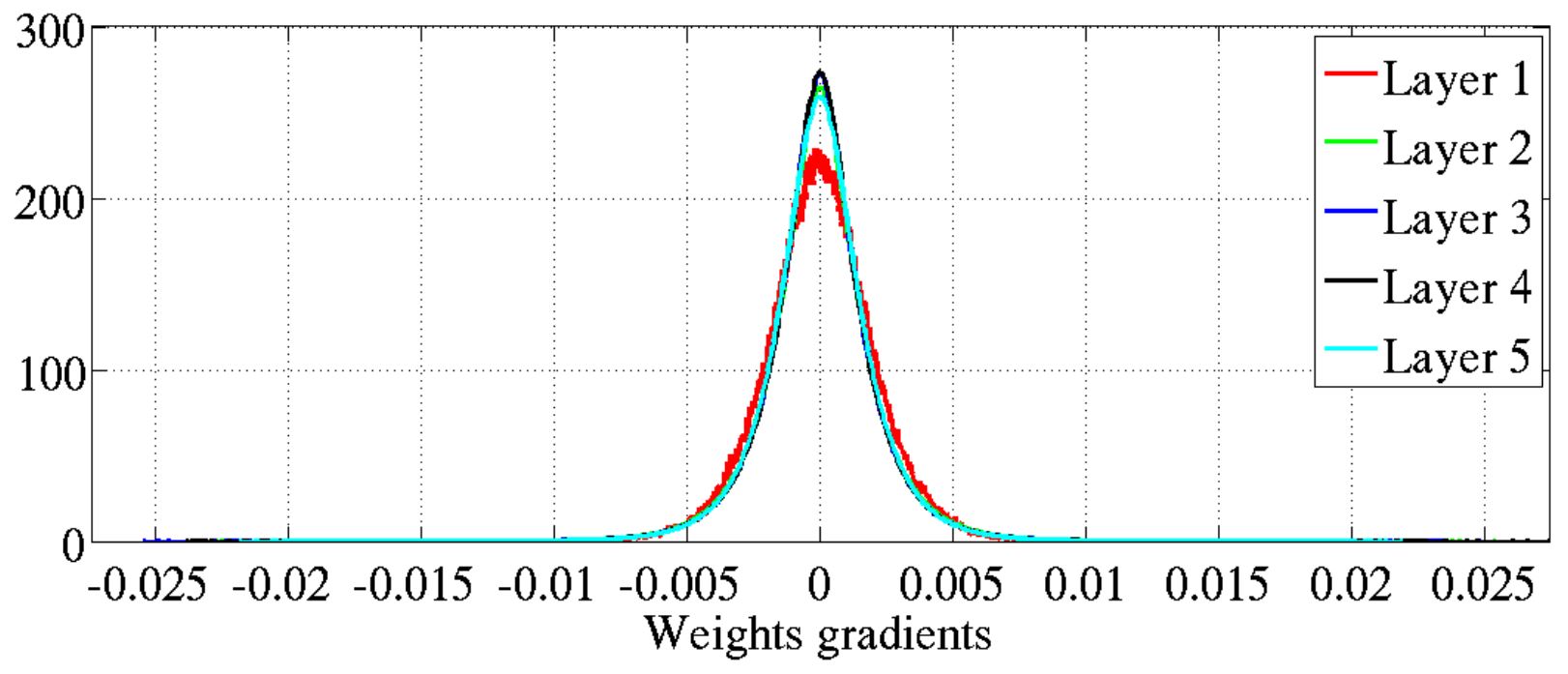
参数梯度的方差和层数基本无关。
参数初始化的几点要求
(1)参数不能全部初始化为$0$,也不能全部初始化同一个值;
(2)最好保证参数初始化的均值为$0$,正负交错,正负参数大致上数量相等;
(3)初始化参数不能太大或者是太小,参数太小会导致特征在每层间逐渐缩小而难以产生作用,参数太大会导致数据在逐层间传递时逐渐放大而导致梯度消失发散,不能训练;
(4)如果有可能满足Glorot条件也是不错的;
上面的几点要求中,(1)(2)(3)基本上是硬性要求,这也就衍生出了一系列的参数初始化方法,什么正态标准化等诸如此类的标准化方法,关于各种参数初始化方法,会在后面继续说明。
常见的参数初始化方法
我们常见的几种初始化方法是按照“正态分布随机初始化——对应为normal”和按照“均匀分布随机初始化——对应为uniform”,这里就不再多说了,这里介绍几种遇见较少的初始化方法。
Xavier初始化方法(又称Glorot初始化)
正态化的Glorot初始化——glorot_normal
Glorot 正态分布初始化器,也称为 Xavier 正态分布初始化器。它从以$0$为中心(均值),标准差为$stddev = sqrt(\frac{2}{fan_{in} + fan_{out}})$的截断正态分布中抽取样本, 其中$fan_{in}$ 和 $fan_{out}$是权重张量的扇入扇出(即输入和输出的单元数目):$$fan_in = chanels_{in} * kernels_{width} * kernels_{height} \\ fan_{out} = chanels_{out} * kernels_{width} * kernels_{height}$$
举个栗子:假设输入网络的一个$28 * 28 * 1$的数据,卷积核$kernels$形状为$3 * 3$,卷积核通道数$chanels$有$32$个(即输出的通道数有$32$个),那么此时有$limit = sqrt(\frac{6}{1 * 3 * 3 + 32 * 3 * 3})$
在keras和tensorflow均有实现,以keras为例: keras.initializers.glorot_normal(seed=None)
标准化的Glorot初始化——glorot_uniform
Glorot 均匀分布初始化器,也称为 Xavier 均匀分布初始化器。它从$[-limit, limit]$中的均匀分布中抽取样本, 其中$limit = sqrt(\frac{6}{fan_{in}] + fan_{out}})$, $fan_{in}$是权值张量中的输入神经元的数量,$fan_{out}$是权重张量的输出神经元的数量。
【有关均匀分布的上下限$limit$取值的详细推导过程请点击:均匀分布】
以keras为例: keras.initializers.glorot_uniform(seed=None)
输出值分布:tanh vs. ReLU(Xavier initialization)
左边是tanh,右边是ReLU。
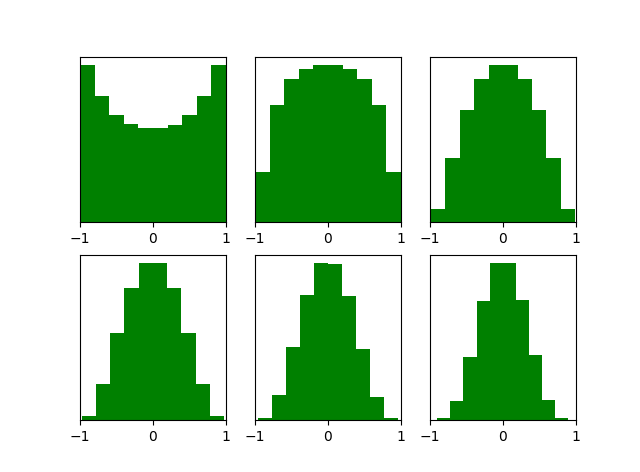
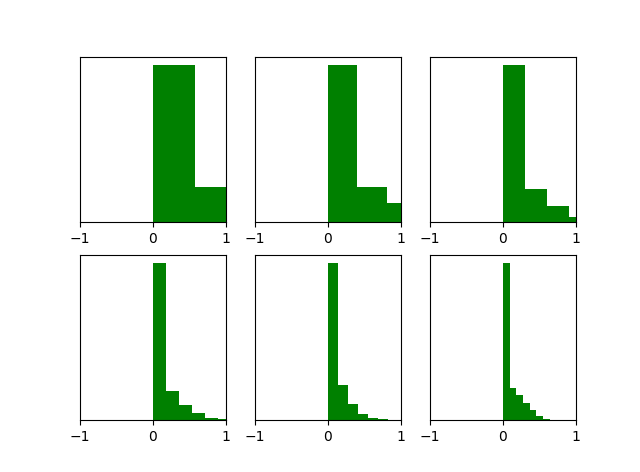
可以看出Xavier搭配tanh,深层的激活函数输出值还是非常漂亮得服从标准高斯分布,但是对于目前神经网络中最常用的ReLU激活函数,还是无能能力,当达到5,6层后几乎又开始趋向于0,更深层的话很明显又会趋向于0。。
Xavier初始化器的缺点
Xavier的推导过程是基于几个假设的,所以这限制了Xavier 初始化器的适用范围。
比如,其中一个假设是激活函数趋近于线性,这并不适用于ReLU等非线性激活函数;
另一个是激活值关于0对称,这个则不适用于sigmoid、ReLU等不是关于0对称的激活函数。
可以实验验证sigmoid激活函数用Xavier初始化后的初始化激活值、反向梯度、参数梯度特性:以MNIST做训练数据,发现标准初始化和Xavier初始化得到的初始激活、参数梯度特性是一样的。激活值的方差逐层递减,参数梯度的方差也逐层递减。
Kaiming初始化(又称He / MSRA初始化)
Kaiming初始化,也称之为He初始化,又称之为MSRA初始化,出自大神何凯明之手。
因为前面讲了Glorot初始化不适合ReLU激活函数,所以残差网络(ResNet)的作者何凯明在Delving Deep into Rectifiers:Surpassing Human-Level Performance on ImageNet Classification文中提出了ReLU网络的初始化方法:Kaming初始化。作者的推导过程针对的其实是卷积网络的前向和反向过程。而为了和Xavier初始化方法保持一致,这里我们还是讨论全连接的网络结构。
关于期望、方差的性质,我们已经在Xavier初始化一节介绍过了,这里不再重复。
在Xavier论文中,作者给出的Glorot条件是:正向传播时,激活值的方差保持不变;反向传播时,关于状态值的梯度的方差保持不变。
这在Kaiming论文中稍作变换:正向传播时,状态值的方差保持不变;反向传播时,关于激活值的梯度的方差保持不变。
正态化的kaiming初始化——he_normal
he正态分布初始化器。它从以$0$为中心,标准差为$stddev = sqrt(\frac{2}{fan_{in}})$的截断正态分布中抽取样本, 其中$fan_{in}$是权值张量中的输入神经元的数量。在keras中的实现为 keras.initializers.he_normal(seed=None)
标准化化的kaiming初始化——he_uniform
he均匀方差缩放初始化器。它从$[-limit, limit]$中的均匀分布中抽取样本, 其中$limit = sqrt(\frac{6}{fan_{in}})$,其中$fan_{in}$是权值张量中的输入神经元的数量。在keras中的实现为 keras.initializers.he_uniform(seed=None)
代码演示
def initialize_parameters_he(layers_dims): """ Arguments: layer_dims -- python array (list) containing the size of each layer. Returns: parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL": W1 -- weight matrix of shape (layers_dims[1], layers_dims[0]) b1 -- bias vector of shape (layers_dims[1], 1) ... WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1]) bL -- bias vector of shape (layers_dims[L], 1) """ np.random.seed(3) parameters = {} L = len(layers_dims) # integer representing the number of layers for l in range(1, L): parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1]) * np.sqrt(2 / layers_dims[l - 1]) parameters['b' + str(l)] = np.zeros((layers_dims[l], 1)) return parameters
经过he initialization后,当隐藏层使用ReLU时,激活函数的输出值的分布情况:
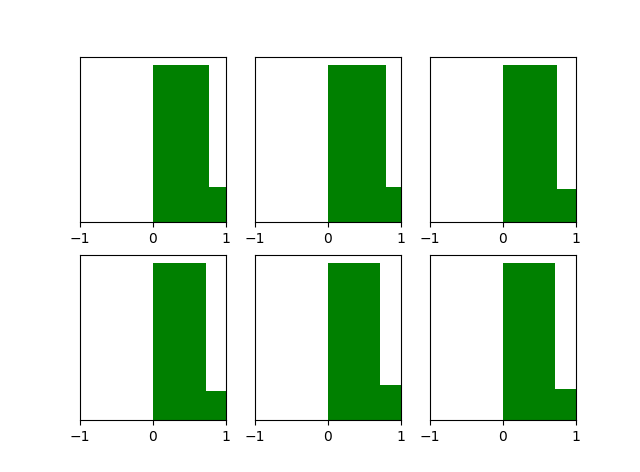
效果是比Xavier initialization好很多。 现在神经网络中,隐藏层常使用ReLU,权重初始化常用He initialization这种方法。
Lecun初始化
出自大神Lecun之手。
正态化的Lecun初始化——lecun_normal
LeCun 正态分布初始化器。它从以$0$为中心,标准差为$stddev = sqrt(\frac{1}{fan_{in}})$的截断正态分布中抽取样本, 其中 fan_in是权值张量中的输入单位的数量。在keras中的实现为 keras.initializers.lecun_normal(seed=None)
标准化的Lecun初始化——lecun_uniform
LeCun 均匀初始化器。它从$[-limit, limit]$中的均匀分布中抽取样本, 其中$limit = sqrt(\frac{3}{fan_{in}})$,$fan_{in}$是权值张量中的输入神经元的数量。在keras中的实现为 keras.initializers.lecun_uniform(seed=None)
Batch Normalization
BN是将输入的数据分布变成高斯分布,这样可以保证每一层神经网络的输入保持相同分布。

优点
随着网络层数的增加,分布逐渐发生偏移,之所以收敛慢,是因为整体分布往非线性函数取值区间的上下限靠近。这会导致反向传播时梯度消失。BN就是通过规范化的手段,把每层神经网络任意神经元这个输入值的分布强行拉回到均值0方差1的标准正态分布,使得激活输入值落入非线性函数中比较敏感的区域。可以让梯度变大,学习收敛速度快,能大大加快收敛速度。
Scale and Shift作用
$\gamma$和$\beta$是学习到的参数,他们可以让标准正态分布变得更高/更胖和向左右偏移。
有关BN的详细解读见深度学习之解密Batch Normalization。
参数初始化方法总结
三种随机初始化器公式汇总

初始化方案建议
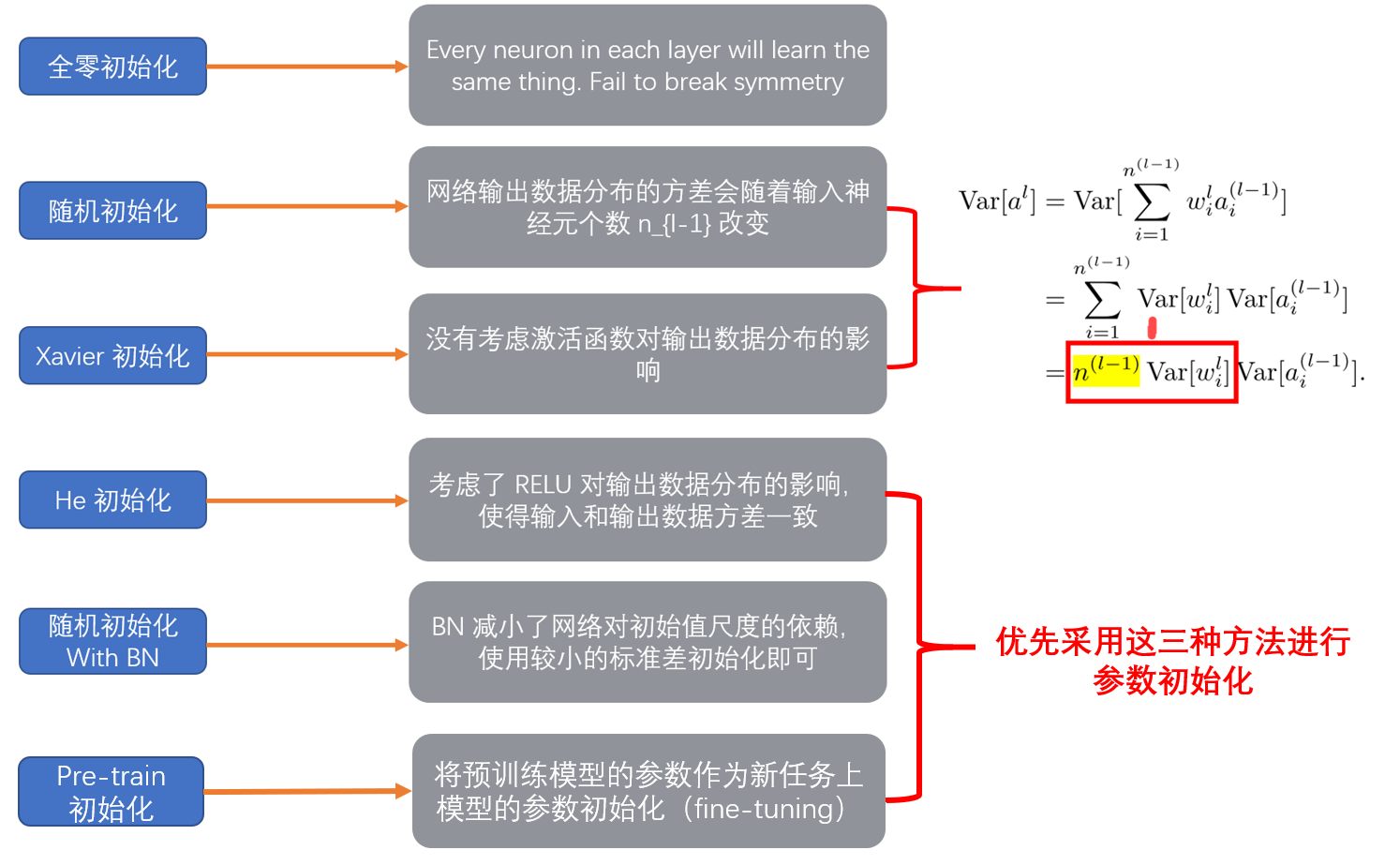
文中代码来自于compare_initialization,感谢作者分享!
参考资料:
https://keras.io/zh/initializers/
https://blog.csdn.net/siyue0211/article/details/80384951
https://blog.csdn.net/u012328159/article/details/80025785




 浙公网安备 33010602011771号
浙公网安备 33010602011771号