数学基础之矩阵求导
本文主要是对刘建平的机器学习中的矩阵向量求导系列文章的整理和转载,并融入了CSDN、知乎等平台上相关文章要点的学习心得,主要参考链接附在文章结尾处。
求导定义与求导布局
矩阵求导引入
在高等数学里面,我们已经学过了标量对标量的求导,比如标量$y$对标量$x$的求导,可以表示为$\frac{\partial y}{\partial x}$。
有些时候,我们会有一组标量$y_i(i = 1, 2,\dots , m)$来对一个标量$x$求导,那么我们会得到一组标量求导的结果:$$\frac{\partial y_i}{\partial x}, i=1,2.,,,m$$
如果我们把这组标量写成向量的形式,即维度为m的一个向量$\mathbf{y}$对一个标量$x$求导,那么结果也是一个m维的向量:$\frac{\partial \mathbf{y}}{\partial x}$。
可见,所谓向量对标量的求导,其实就是向量里的每个分量分别对标量求导,最后把求导的结果排列在一起,按一个向量表示而已。类似的结论也存在于标量对向量的求导,向量对向量的求导,向量对矩阵的求导,矩阵对向量的求导,以及矩阵对矩阵的求导等。
总而言之,所谓的矩阵向量求导本质上就是多元函数求导,仅仅是把函数的自变量,因变量以及标量求导的结果排列成了向量矩阵的形式,方便表达与计算,更加简洁而已。
为了便于描述,后面如果没有指明,则求导的自变量用$x$表示标量,$\mathbf{x}$表示n维向量,$\mathbf{X}$表示$m \times n$维度的矩阵,求导的因变量用$y$表示标量,$\mathbf{y}$表示m维向量,$\mathbf{Y}$表示$p \times q$维度的矩阵。
矩阵求导定义
根据求导的自变量和因变量是标量,向量还是矩阵,我们有9种可能的矩阵求导定义,如下:
| 自变量\因变量 | 标量$y$ | 向量$\mathbf{y}$ | 矩阵$\mathbf{Y}$ |
| 标量$x$ | $\frac{\partial y}{\partial x}$ | $\frac{\partial \mathbf{y}}{\partial x}$ | $\frac{\partial \mathbf{Y}}{\partial x}$ |
| 向量$\mathbf{x}$ | $\frac{\partial y}{\partial \mathbf{x}}$ | $\frac{\partial \mathbf{y}}{\partial \mathbf{x}}$ | $\frac{\partial \mathbf{Y}}{\partial \mathbf{x}}$ |
| 矩阵$\mathbf{X}$ | $\frac{\partial y}{\partial \mathbf{X}}$ | $\frac{\partial \mathbf{y}}{\partial \mathbf{X}}$ | $\frac{\partial \mathbf{Y}}{\partial \mathbf{X}}$ |
这9种里面,标量对标量的求导高数里面就有,不需要我们单独讨论,在剩下的8种情况里面,本节先讨论上图中标量对向量或矩阵求导,向量或矩阵对标量求导,以及向量对向量求导这5种情况。另外三种向量对矩阵的求导,矩阵对向量的求导,以及矩阵对矩阵的求导在第3节再讲。
现在我们回看前面讲到的例子,维度为m的一个向量$\mathbf{y}$对一个标量$x$的求导,那么结果也是一个m维的向量:$\frac{\partial \mathbf{y}}{\partial x}$。这是我们表格里面向量对标量求导的情况。这里有一个问题没有讲到,就是这个m维的求导结果排列成的m维向量到底应该是列向量还是行向量?
这个问题的答案是:行向量或者列向量皆可!毕竟我们求导的本质只是把标量求导的结果排列起来,至于是按行排列还是按列排列都是可以的。但是这样也有问题,在我们机器学习算法法优化过程中,如果行向量或者列向量随便写,那么结果就不唯一,乱套了。
为了解决这个问题,我们引入求导布局的概念。
矩阵向量求导布局
为了解决矩阵向量求导的结果不唯一,我们引入求导布局。最基本的求导布局有两个:分子布局(numerator layout)和分母布局(denominator layout )。
- 对于分子布局来说,我们求导结果的维度以分子为主,比如对于我们上面对标量求导的例子,结果的维度和分子的维度是一致的。也就是说,如果向量$\mathbf{y}$是一个m维的列向量,那么求导结果$\frac{\partial \mathbf{y}}{\partial x}$也是一个m维列向量。如果向量$\mathbf{y}$是一个m维的行向量,那么求导结果$\frac{\partial \mathbf{y}}{\partial x}$也是一个m维行向量。
- 对于分母布局来说,我们求导结果的维度以分母为主,比如对于我们上面对标量求导的例子,如果向量$\mathbf{y}$是一个m维的列向量,那么求导结果$\frac{\partial \mathbf{y}}{\partial x}$是一个m维行向量。如果向量$\mathbf{y}$是一个m维的行向量,那么求导结果$\frac{\partial \mathbf{y}}{\partial x}$是一个m维的列向量向量。
可见,对于分子布局和分母布局的结果来说,两者相差一个转置。
再举一个例子,标量$y$对矩阵$ \mathbf{X}$求导,那么如果按分母布局,则求导结果的维度和矩阵$X$的维度$m \times n$是一致的。如果是分子布局,则求导结果的维度为$n \times m$。
这样,对于标量对向量或者矩阵求导,向量或者矩阵对标量求导这4种情况,对应的分子布局和分母布局的排列方式已经确定了。
稍微麻烦点的是向量对向量的求导,本文只讨论列向量对列向量的求导,其他的行向量求导只是差一个转置而已。比如m维列向量$\mathbf{y}$对n维列向量$\mathbf{x}$求导,它的求导结果在分子布局和分母布局各是什么呢?
对于这2个向量求导,那么一共有$mn$个标量对标量的求导。求导的结果一般是排列为一个矩阵。如果是分子布局,则矩阵的第一个维度以分子为准,即结果是一个$m \times n$的矩阵,如下:$$ \frac{\partial \mathbf{y}}{\partial \mathbf{x}} = \left( \begin{array}{ccc} \frac{\partial y_1}{\partial x_1}& \frac{\partial y_1}{\partial x_2}& \ldots & \frac{\partial y_1}{\partial x_n}\\ \frac{\partial y_2}{\partial x_1}& \frac{\partial y_2}{\partial x_2} & \ldots & \frac{\partial y_2}{\partial x_n}\\ \vdots& \vdots & \ddots & \vdots \\ \frac{\partial y_m}{\partial x_1}& \frac{\partial y_m}{\partial x_2} & \ldots & \frac{\partial y_m}{\partial x_n} \end{array} \right)$$
上边这个按分子布局的向量对向量求导的结果矩阵,我们一般叫做雅克比 (Jacobian)矩阵。
如果是按分母布局,则求导的结果矩阵的第一维度会以分母为准,即结果是一个$n \times m$的矩阵,如下:$$ \frac{\partial \mathbf{y}}{\partial \mathbf{x}} = \left( \begin{array}{ccc} \frac{\partial y_1}{\partial x_1}& \frac{\partial y_2}{\partial x_1}& \ldots & \frac{\partial y_m}{\partial x_1}\\ \frac{\partial y_1}{\partial x_2}& \frac{\partial y_2}{\partial x_2} & \ldots & \frac{\partial y_m}{\partial x_2}\\ \vdots& \vdots & \ddots & \vdots \\ \frac{\partial y_1}{\partial x_n}& \frac{\partial y_2}{\partial x_n} & \ldots & \frac{\partial y_m}{\partial x_n} \end{array} \right)$$
上边这个按分母布局的向量对向量求导的结果矩阵,我们一般叫做梯度矩阵。
有了布局的概念,我们对于上面5种求导类型,可以各选择一种布局来求导。但是对于某一种求导类型,不能同时使用分子布局和分母布局求导。
但是在机器学习算法原理的资料推导里,我们并没有看到说正在使用什么布局,也就是说布局被隐含了,这就需要自己去推演,比较麻烦。但是一般来说我们会使用一种叫混合布局的思路,即如果是向量或者矩阵对标量求导,则使用分子布局为准,如果是标量对向量或者矩阵求导,则以分母布局为准。对于向量对对向量求导,有些分歧,本文中会以分子布局的雅克比矩阵为主。
具体总结如下:
| 自变量\因变量 | 标量$y$ | 列向量$\mathbf{y}$ | 矩阵$\mathbf{Y}$ |
| 标量$x$ | / |
$\frac{\partial \mathbf{y}}{\partial x}$ 分子布局:m维列向量(默认布局) 分母布局:m维行向量 |
$\frac{\partial \mathbf{Y}}{\partial x}$ 分子布局:$p \times q$矩阵(默认布局) 分母布局:$q \times p$矩阵 |
| 列向量$\mathbf{x}$ |
$\frac{\partial y}{\partial \mathbf{x}}$ 分子布局:n维行向量 分母布局:n维列向量(默认布局) |
$\frac{\partial \mathbf{y}}{\partial \mathbf{x}}$ 分子布局:$m \times n$雅克比矩阵(默认布局) 分母布局:$n \times m$梯度矩阵 |
/ |
| 矩阵$\mathbf{X}$ |
$\frac{\partial y}{\partial \mathbf{X}}$ 分子布局:$n \times m$矩阵 分母布局:$m \times n$矩阵(默认布局) |
/ | / |
矩阵向量求导基础总结
有了矩阵向量求导的定义和默认布局,我们后续就可以对上表中的5种矩阵向量求导过程进行一些常见的求导推导并总结求导方法,并讨论向量求导的链式法则。
定义法
上一节主要讨论了向量矩阵求导的9种定义与求导布局的概念。本节就其中的标量对向量求导,标量对矩阵求导, 以及向量对向量求导这三种场景的基本求解思路进行讨论。
对于本文中的标量对向量或矩阵求导这两种情况,如上节所说,以分母布局为默认布局。向量对向量求导,以分子布局为默认布局。如遇到其他文章中的求导结果和本文不同,请先确认使用的求导布局是否一样。另外,由于机器学习中向量或矩阵对标量求导的场景很少见,本文不会单独讨论这两种求导过程。
用定义法求解标量对向量求导
标量对向量求导,严格来说是实值函数对向量的求导。即定义实值函数$f: R^{n} \to R$,自变量$\mathbf{x}$是n维向量,而输出$y$是标量。对于一个给定的实值函数,如何求解$\frac{\partial y}{\partial \mathbf{x}}$呢?
首先我们想到的是基于矩阵求导的定义来做,由于所谓标量对向量的求导,其实就是标量对向量里的每个分量分别求导,最后把求导的结果排列在一起,按一个向量表示而已。那么我们可以将实值函数对向量的每一个分量来求导,最后找到规律,得到求导的结果向量。
首先我们来看一个简单的例子:$y=\mathbf{a}^T\mathbf{x}$,求解$\frac{\partial \mathbf{a}^T\mathbf{x}}{\partial \mathbf{x}}$
根据定义,我们先对$\mathbf{x}$的第i个分量进行求导,这是一个标量对标量的求导,如下:$$\frac{\partial \mathbf{a}^T\mathbf{x}}{\partial x_i} = \frac{\partial \sum\limits_{j=1}^n a_jx_j}{\partial x_i} = \frac{\partial a_ix_i}{\partial x_i} =a_i$$
可见,对向量的第i个分量的求导结果就等于向量$\mathbf{a}$的第i个分量。由于我们是分子布局,最后所有求导结果的分量组成的是一个n维向量。那么其实就是向量$\mathbf{a}$。也就是说:$$\frac{\partial \mathbf{a}^T\mathbf{x}}{\partial \mathbf{x}} = \mathbf{a}$$
同样的思路,我们也可以直接得到:$$\frac{\partial \mathbf{x}^T\mathbf{a}}{\partial \mathbf{x}} = \mathbf{a}$$
给一个简单的测试,大家看看自己能不能按定义法推导出:$$\frac{\partial \mathbf{x}^T\mathbf{x}}{\partial \mathbf{x}} =2\mathbf{x}$$
再来看一个复杂一点点的例子:$y=\mathbf{x}^T\mathbf{A}\mathbf{x}$,求解$\frac{\partial \mathbf{x}^T\mathbf{A}\mathbf{x}}{\partial \mathbf{x}}$
我们对$\mathbf{x}$的第k个分量进行求导如下:$$\frac{\partial \mathbf{x}^T\mathbf{A}\mathbf{x}}{\partial x_k} = \frac{\partial \sum\limits_{i=1}^n\sum\limits_{j=1}^n x_iA_{ij}x_j}{\partial x_k} = \sum\limits_{i=1}^n A_{ik}x_i + \sum\limits_{j=1}^n A_{kj}x_j $$
这个第k个分量的求导结果稍微复杂些了,仔细观察一下,第一部分是矩阵$\mathbf{A}$的第k列转置后和$x$相乘得到,第二部分是矩阵$\mathbf{A}$的第k行和$x$相乘得到,排列好就是: $$\frac{\partial \mathbf{x}^T\mathbf{A}\mathbf{x}}{\partial \mathbf{x}} = \mathbf{A}^T\mathbf{x} + \mathbf{A}\mathbf{x}$$
从上面可以看出,定义法求导对于简单的实值函数是很容易的,但是复杂的实值函数就算求出了任意一个分量的导数,要排列出最终的求导结果还挺麻烦的,因此我们需要找到其他的简便一些的方法来整体求导,而不是每次都先去针对任意一个分量,再进行排列。
标量对向量求导的一些基本法则
在我们寻找一些简单的方法前,我们简单看下标量对向量求导的一些基本法则,这些法则和标量对标量求导的过程类似。
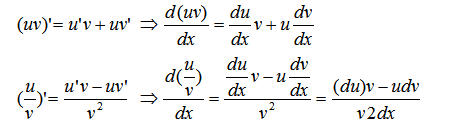
1) 常量对向量的求导结果为0。
2) 线性法则:如果$f,g$都是实值函数,$c_1,c_2$为常数,则:$$\frac{\partial (c_1f(\mathbf{x})+c_2g(\mathbf{x})}{\partial \mathbf{x}} = c_1\frac{\partial f(\mathbf{x})}{\partial \mathbf{x}} +c_2\frac{\partial g(\mathbf{x})}{\partial \mathbf{x}} $$
3) 乘法法则:如果$f,g$都是实值函数,则:$$\frac{\partial f(\mathbf{x})g(\mathbf{x})}{\partial \mathbf{x}} = f(\mathbf{x})\frac{\partial g(\mathbf{x})}{\partial \mathbf{x}} +\frac{\partial f(\mathbf{x})}{\partial \mathbf{x}} g(\mathbf{x}) $$
要注意的是如果不是实值函数,则不能这么使用乘法法则。
4) 除法法则:如果$f,g$都是实值函数,且$g(\mathbf{x}) \neq 0$,则:$$\frac{\partial f(\mathbf{x})/g(\mathbf{x})}{\partial \mathbf{x}} = \frac{1}{g^2(\mathbf{x})}(g(\mathbf{x})\frac{\partial f(\mathbf{x})}{\partial \mathbf{x}} - f(\mathbf{x})\frac{\partial g(\mathbf{x})}{\partial \mathbf{x}})$$
用定义法求解标量对矩阵求导
现在我们来看看定义法如何解决标量对矩阵的求导问题。其实思路和2.2的标量对向量的求导是类似的,只是最后的结果是一个和自变量同型的矩阵。
我们还是以一个例子来说明。$y=\mathbf{a}^T\mathbf{X}\mathbf{b}$,求解$\frac{\partial \mathbf{a}^T\mathbf{X}\mathbf{b}}{\partial \mathbf{X}}$
其中, $\mathbf{a}$是m维向量,$\mathbf{b}$是n维向量, $\mathbf{X}$是$m \times n$的矩阵。
我们对矩阵$\mathbf{X}$的任意一个位置的$X_{ij}$求导,如下:$$\frac{\partial \mathbf{a}^T\mathbf{X}\mathbf{b}}{\partial X_{ij}} = \frac{\partial \sum\limits_{p=1}^m\sum\limits_{q=1}^n a_pA_{pq}b_q}{\partial X_{ij}} = \frac{\partial a_iA_{ij}b_j}{\partial X_{ij}} = a_ib_j$$
即求导结果在$(i.j)$位置的求导结果是$\mathbf{a}$向量第i个分量和$\mathbf{b}$第j个分量的乘积,将所有的位置的求导结果排列成一个$m \times n$的矩阵,即为$ab^T$,这样最后的求导结果为:$$\frac{\partial \mathbf{a}^T\mathbf{X}\mathbf{b}}{\partial \mathbf{X}} = ab^T$$
简单的求导的确不难,但是如果是比较复杂的标量对矩阵求导,比如$y=\mathbf{a}^Texp(\mathbf{X}\mathbf{b})$,对任意标量求导容易,排列起来还是蛮麻烦的,也就是我们遇到了和标量对向量求导一样的问题,定义法比较适合解决简单的问题,复杂的求导需要更简便的方法。这个方法我们在下一节来讲。
同时,标量对矩阵求导也有和第二节对向量求导类似的基本法则,这里就不累述了。
用定义法求解向量对向量求导
这里我们也同样给出向量对向量求导的定义法的具体例子。
先来一个简单的例子: $\mathbf{y} = \mathbf{A} \mathbf{x} $,其中$ \mathbf{A}$为$n \times m$的矩阵。$\mathbf{x}, \mathbf{y}$分别为$m,n$维向量。需要求导$\frac{\partial \mathbf{A}\mathbf{x}}{\partial \mathbf{x}}$,根据定义,结果应该是一个$n \times m$的矩阵。
先求矩阵的第i行和向量的内积对向量的第j分量求导,用定义法求解过程如下:$$\frac{\partial \mathbf{A_i}\mathbf{x}}{\partial \mathbf{x_j}} = \frac{\partial A_{ij}x_j}{\partial \mathbf{x_j}}= A_{ij}$$
可见矩阵 $\mathbf{A}$的第i行和向量的内积对向量的第j分量求导的结果就是矩阵 $\mathbf{A}$的$(i,j)$位置的值。排列起来就是一个矩阵了,由于我们分子布局,所以排列出的结果是$ \mathbf{A}$,而不是 $\mathbf{A}^T$。
定义法矩阵向量求导的局限
使用定义法虽然已经求出一些简单的向量矩阵求导的结果,但是对于复杂的求导式子,则中间运算会很复杂,同时求导出的结果排列也是很头痛的。下一节我们讨论使用矩阵微分和迹函数的方法来求解矩阵向量求导。
矩阵向量求导之微分法
第2节主要讨论了定义法求解矩阵向量求导的方法,但是这个方法对于比较复杂的求导式子,中间运算会很复杂,同时排列求导出的结果也很麻烦。因此我们需要其他的一些求导方法。本节我们讨论使用微分法来求解标量对向量的求导,以及标量对矩阵的求导。
本文的标量对向量的求导,以及标量对矩阵的求导使用分母布局。如果遇到其他资料求导结果不同,请先确认布局是否一样。
矩阵微分
在高数里面我们学习过标量的导数和微分,它们之间有这样的关系:$\mathrm{d}f = f'(x)\mathrm{d}x$。如果是多变量的情况,则微分可以写成:$$df=\sum\limits_{i=1}^n\frac{\partial f}{\partial x_i}dx_i = (\frac{\partial f}{\partial \mathbf{x}})^Td\mathbf{x}$$
从上次我们可以发现标量对向量的求导和它的向量微分有一个转置的关系。
现在我们再推广到矩阵。对于矩阵微分,我们的定义为:$$df=\sum\limits_{i=1}^m\sum\limits_{j=1}^n\frac{\partial f}{\partial X_{ij}}dX_{ij} = tr((\frac{\partial f}{\partial \mathbf{X}})^Td\mathbf{X})$$
其中第二步使用了矩阵迹的性质,即迹函数等于主对角线的和。即$$tr(A^TB) = \sum\limits_{i,j}A_{ij}B_{ij}$$
【推导注释:矩阵微分到迹函数的详细推导请点】
从上面矩阵微分的式子,我们可以看到矩阵微分和它的导数也有一个转置的关系,不过在外面套了一个迹函数而已。由于标量的迹函数就是它本身,那么矩阵微分和向量微分可以统一表示,即:$$df= tr((\frac{\partial f}{\partial \mathbf{X}})^Td\mathbf{X})\;\; \;df= tr((\frac{\partial f}{\partial \mathbf{x}})^Td\mathbf{x})$$
矩阵微分的性质
我们在讨论如何使用矩阵微分来求导前,先看看矩阵微分的性质:
1) 微分加减法:$d(X+Y) =dX+dY, d(X-Y) =dX-dY$
2) 微分乘法:$d(XY) =(dX)Y + X(dY)$
3) 微分转置:$d(X^T) =(dX)^T$
4) 微分的迹:$dtr(X) =tr(dX)$
5) 微分哈达马乘积: $d(X \odot Y) = X\odot dY + dX \odot Y$
6) 逐元素求导:$d \sigma(X) =\sigma'(X) \odot dX$
【公式注解:这里的$\sigma ()$是逐元素求导,即是对$X$中的每个元素各自做变换的函数。附哈达马乘积详解】
7) 逆矩阵微分:$d X^{-1}= -X^{-1}dXX^{-1}$
8) 行列式微分:$d |X|= |X|tr(X^{-1}dX)$
【公式注解:行列式的导数】
有了这些性质,我们再来看看如何由矩阵微分来求导数。
使用微分法求解矩阵向量求导
由于3.1我们已经得到了矩阵微分和导数关系,现在我们就来使用微分法求解矩阵向量求导。
若标量函数$f$是矩阵$X$经加减乘法、逆、行列式、逐元素函数等运算构成,则使用相应的运算法则对$f$求微分,再使用迹函数技巧给$df$套上迹并将其它项交换至$dX$左侧,那么对于迹函数里面在$dX$左边的部分,我们只需要加一个转置就可以得到导数了。
这里需要用到的迹函数的技巧主要有这么几个:
1) 标量的迹等于自己:$tr(x) =x$
2) 转置不变:$tr(A^T) =tr(A)$
3) 交换率:$tr(AB) =tr(BA)$,需要满足$A,B^T$同维度。
4) 加减法:$tr(X+Y) =tr(X)+tr(Y), tr(X-Y) =tr(X)-tr(Y)$
5) 矩阵乘法和迹交换:$tr((A\odot B)^TC)= tr(A^T(B \odot C))$,需要满足$A,B,C$同维度。
我们先看第一个例子,我们使用上一篇定义法中的一个求导问题:$$y=\mathbf{a}^T\mathbf{X}\mathbf{b}, \frac{\partial y}{\partial \mathbf{X}}$$
首先,我们使用微分乘法的性质对$f$求微分,得到:$$dy = d\mathbf{a}^T\mathbf{X}\mathbf{b} + \mathbf{a}^Td\mathbf{X}\mathbf{b} + \mathbf{a}^T\mathbf{X}d\mathbf{b} = \mathbf{a}^Td\mathbf{X}\mathbf{b}$$ 【推导注解:常量的微分为0】
第二步,就是两边套上迹函数,即:$$dy =tr(dy) = tr(\mathbf{a}^Td\mathbf{X}\mathbf{b}) = tr(\mathbf{b}\mathbf{a}^Td\mathbf{X})$$
其中第一到第二步使用了上面迹函数性质1,第三步到第四步用到了上面迹函数的性质3。
根据我们矩阵导数和微分的定义,迹函数里面在$dX$左边的部分$\mathbf{b}\mathbf{a}^T$,加上一个转置即为我们要求的导数,即:$$\frac{\partial f}{\partial \mathbf{X}} = (\mathbf{b}\mathbf{a}^T)^T = \mathbf{ab}^T$$
以上就是微分法的基本流程,先求微分再做迹函数变换,最后得到求导结果。比起定义法,我们现在不需要去对矩阵中的单个标量进行求导了。
再来看看$$y=\mathbf{a}^Texp(\mathbf{X}\mathbf{b}), \frac{\partial y}{\partial \mathbf{X}}$$
$$dy =tr(dy) = tr(\mathbf{a}^Tdexp(\mathbf{X}\mathbf{b})) = tr(\mathbf{a}^T (exp(\mathbf{X}\mathbf{b}) \odot d(\mathbf{X}\mathbf{b}))) = tr((\mathbf{a} \odot exp(\mathbf{X}\mathbf{b}) )^T d\mathbf{X}\mathbf{b}) = tr(\mathbf{b}(\mathbf{a} \odot exp(\mathbf{X}\mathbf{b}) )^T d\mathbf{X}) $$
其中第三步到第四步使用了上面迹函数的性质5。【推导注解:$exp(x)$的导数是其本身】
这样我们的求导结果为:$$\frac{\partial y}{\partial \mathbf{X}} =(\mathbf{a} \odot exp(\mathbf{X}\mathbf{b}) )b^T $$
以上就是微分法的基本思路。
【推导注解:标量的迹等于自身,所以标量函数的微分都可以直接套上迹来算】
迹函数对向量矩阵求导
由于微分法使用了迹函数的技巧,那么迹函数对对向量矩阵求导这一大类问题,使用微分法是最简单直接的。下面给出一些常见的迹函数的求导过程,也顺便给大家熟练掌握微分法的技巧。
首先是$\frac{\partial tr(AB)}{\partial A} = B^T, \frac{\partial tr(AB)}{\partial B} =A^T$,这个直接根据矩阵微分的定义即可得到。
再来看看$\frac{\partial tr(W^TAW)}{\partial W}$:$$d(tr(W^TAW)) = tr(dW^TAW +W^TAdW) = tr(dW^TAW)+tr(W^TAdW) = tr((dW)^TAW) + tr(W^TAdW) = tr(W^TA^TdW) + tr(W^TAdW) = tr(W^T(A+A^T)dW) $$
因此可以得到:$$\frac{\partial tr(W^TAW)}{\partial W} = (A+A^T)W$$
最后来个更加复杂的迹函数求导:$\frac{\partial tr(B^TX^TCXB)}{\partial X} $: $$d(tr(B^TX^TCXB)) = tr(B^TdX^TCXB) + tr(B^TX^TCdXB) = tr((dX)^TCXBB^T) + tr(BB^TX^TCdX) = tr(BB^TX^TC^TdX) + tr(BB^TX^TCdX) = tr((BB^TX^TC^T + BB^TX^TC)dX)$$
因此可以得到:$$\frac{\partial tr(B^TX^TCXB)}{\partial X}= (C+C^T)XBB^T$$
【推导注解:多次用到了迹函数转置不变的技巧】
微分法求导小结
使用矩阵微分,可以在不对向量或矩阵中的某一元素单独求导再拼接,因此会比较方便,当然熟练使用的前提是对上面矩阵微分的性质,以及迹函数的性质熟练运用。
【结论注解:对于未提及的向量对向量求导在分母布局时与微分存在转置关系,而在分子布局时相等。】
还有一些场景,求导的自变量和因变量直接有复杂的多层链式求导的关系,此时微分法使用起来也有些麻烦。如果我们可以利用一些常用的简单求导结果,再使用链式求导法则,则会非常的方便。因此下一节我们讨论向量矩阵求导的链式法则。
矩阵向量求导链式法则
第3节讨论了使用微分法来求解矩阵向量求导的方法。但是很多时候,求导的自变量和因变量直接有复杂的多层链式求导的关系,此时微分法使用起来也有些麻烦。需要一些简洁的方法。本文我们讨论矩阵向量求导链式法则,使用该法则很多时候可以帮我们快速求出导数结果。
本节的标量对向量的求导,标量对矩阵的求导使用分母布局, 向量对向量的求导使用分子布局。如果遇到其他资料求导结果不同,请先确认布局是否一样。
向量对向量求导的链式法则
首先我们来看看向量对向量求导的链式法则。假设多个向量存在依赖关系,比如三个向量$\mathbf{x} \to \mathbf{y} \to \mathbf{z}$存在依赖关系,则我们有下面的链式求导法则:$$\frac{\partial \mathbf{z}}{\partial \mathbf{x}} = \frac{\partial \mathbf{z}}{\partial \mathbf{y}}\frac{\partial \mathbf{y}}{\partial \mathbf{x}}$$
该法则也可以推广到更多的向量依赖关系。但是要注意的是要求所有有依赖关系的变量都是向量,如果有一个$\mathbf{Y}$是矩阵,,比如是$\mathbf{x} \to \mathbf{Y} \to \mathbf{z}$, 则上式并不成立。
从矩阵维度相容的角度也很容易理解上面的链式法则,假设$\mathbf{x} , \mathbf{y} ,\mathbf{z}$分别是$m, n, p$维向量,则求导结果$\frac{\partial \mathbf{z}}{\partial \mathbf{x}}$是一个$p \times m$的雅克比矩阵,而右边$\frac{\partial \mathbf{z}}{\partial \mathbf{y}}$是一个$p \times n$的雅克比矩阵,$\frac{\partial \mathbf{y}}{\partial \mathbf{x}}$是一个$n \times m$的矩阵,两个雅克比矩阵的乘积维度刚好是$p \times m$,和左边相容。
标量对多个向量的链式求导法则
在我们的机器学习算法中,最终要优化的一般是一个标量损失函数,因此最后求导的目标是标量,无法使用上面的链式求导法则,比如2向量,最后到1标量的依赖关系:$\mathbf{x} \to \mathbf{y} \to z$,此时很容易发现维度不相容。
假设$\mathbf{x} , \mathbf{y} $分别是$m,n$维向量, 那么$\frac{\partial z}{\partial \mathbf{x}}$的求导结果是一个$m \times 1$的向量, 而$\frac{\partial z}{\partial \mathbf{y}}$是一个$n \times 1$的向量,$\frac{\partial \mathbf{y}}{\partial \mathbf{x}}$是一个$n \times m$的雅克比矩阵,右边的向量和矩阵是没法直接乘的。
但是假如我们把标量求导的部分都做一个转置,那么维度就可以相容了,也就是:$$(\frac{\partial z}{\partial \mathbf{x}})^T = (\frac{\partial z}{\partial \mathbf{y}})^T\frac{\partial \mathbf{y}}{\partial \mathbf{x}} $$
但是毕竟我们要求导的是$(\frac{\partial z}{\partial \mathbf{x}})$,而不是它的转置,因此两边转置我们可以得到标量对多个向量求导的链式法则:$$\frac{\partial z}{\partial \mathbf{x}} = (\frac{\partial \mathbf{y}}{\partial \mathbf{x}} )^T\frac{\partial z}{\partial \mathbf{y}}$$
如果是标量对更多的向量求导,比如$\mathbf{y_1} \to \mathbf{y_2} \to …\to \mathbf{y_n} \to z$,则其链式求导表达式可以表示为:$$\frac{\partial z}{\partial \mathbf{y_1}} = (\frac{\partial \mathbf{y_n}}{\partial \mathbf{y_{n-1}}} \frac{\partial \mathbf{y_{n-1}}}{\partial \mathbf{y_{n-2}}} …\frac{\partial \mathbf{y_2}}{\partial \mathbf{y_1}})^T\frac{\partial z}{\partial \mathbf{y_n}}$$
这里我们给一个最常见的最小二乘法求导的例子。最小二乘法优化的目标是最小化如下损失函数:$$l=(X\theta – y)^T(X\theta – y)$$
我们优化的损失函数$l$是一个标量,而模型参数$\theta$是一个向量,期望$\ell$对$\theta$求导,并求出导数等于0时候的极值点。我们假设向量$z = X\theta – y$, 则$l=z^Tz$, $\theta \to z \to l$存在链式求导的关系,因此:$$\frac{\partial l}{\partial \mathbf{\theta}} = (\frac{\partial z}{\partial \theta} )^T\frac{\partial l}{\partial \mathbf{z}} = X^T(2z) =2X^T(X\theta – y)$$
其中最后一步转换使用了如下求导公式:$$\frac{\partial X\theta – y}{\partial \theta} = X$$ $$\frac{\partial z^Tz}{\partial z} = 2z$$
这两个式子我们在前几篇里已有求解过,现在可以直接拿来使用了,非常方便。
当然上面的问题使用微分法求导数也是非常简单的,这里只是给出链式求导法的思路。
标量对多个矩阵的链式求导法则
下面我们再来看看标量对多个矩阵的链式求导法则,假设有这样的依赖关系:$\mathbf{X} \to \mathbf{Y} \to z$,那么我们有:$$\frac{\partial z}{\partial x_{ij}} = \sum\limits_{k,l}\frac{\partial z}{\partial Y_{kl}} \frac{\partial Y_{kl}}{\partial X_{ij}} =tr((\frac{\partial z}{\partial Y})^T\frac{\partial Y}{\partial X_{ij}})$$
这里大家会发现我们没有给出基于矩阵整体的链式求导法则,主要原因是矩阵对矩阵的求导是比较复杂的定义,我们目前也未涉及。因此只能给出对矩阵中一个标量的链式求导方法。这个方法并不实用,因为我们并不想每次都基于定义法来求导最后再去排列求导结果。
虽然我们没有全局的标量对矩阵的链式求导法则,但是对于一些线性关系的链式求导,我们还是可以得到一些有用的结论的。
【神经网络经典范例】
我们来看这个常见问题:$A,X,B,Y$都是矩阵,$z$是标量,其中$z= f(Y), Y=AX+B$,我们要求出$\frac{\partial z}{\partial X}$,这个问题在机器学习中是很常见的。此时,我们并不能直接整体使用矩阵的链式求导法则,因为矩阵对矩阵的求导结果不好处理。
这里我们回归初心,使用定义法试一试,先使用上面的标量链式求导公式:$$\frac{\partial z}{\partial x_{ij}} = \sum\limits_{k,l}\frac{\partial z}{\partial Y_{kl}} \frac{\partial Y_{kl}}{\partial X_{ij}}$$
我们再来看看后半部分的导数:$$ \frac{\partial Y_{kl}}{\partial X_{ij}} = \frac{\partial \sum\limits_s(A_{ks}X_{sl})}{\partial X_{ij}} = \frac{\partial A_{ki}X_{il}}{\partial X_{ij}} =A_{ki}\delta_{lj}$$
其中$\delta_{lj}$在$l = j$时为$1$,否则为$0$。
那么最终的标签链式求导公式转化为:$$\frac{\partial z}{\partial x_{ij}} = \sum\limits_{k,l}\frac{\partial z}{\partial Y_{kl}} A_{ki}\delta_{lj} = \sum\limits_{k}\frac{\partial z}{\partial Y_{kj}} A_{ki}$$
即矩阵$A^T$的第i行和$\frac{\partial z}{\partial Y} $的第j列的内积。排列成矩阵即为:$$\frac{\partial z}{\partial X} = A^T\frac{\partial z}{\partial Y}$$
总结下就是:$$z= f(Y), Y=AX+B \to \frac{\partial z}{\partial X} = A^T\frac{\partial z}{\partial Y}$$
这结论在$\mathbf{x}$是一个向量的时候也成立,即:$$z= f(\mathbf{y}), \mathbf{y}=A\mathbf{x}+\mathbf{b} \to \frac{\partial z}{\partial \mathbf{x}} = A^T\frac{\partial z}{\partial \mathbf{y}}$$
如果要求导的自变量在左边,线性变换在右边,也有类似稍有不同的结论如下,证明方法是类似的,这里直接给出结论:$$z= f(Y), Y=XA+B \to \frac{\partial z}{\partial X} = \frac{\partial z}{\partial Y}A^T$$ $$z= f(\mathbf{y}), \mathbf{y}=X\mathbf{a}+\mathbf{b} \to \frac{\partial z}{\partial \mathbf{X}} = \frac{\partial z}{\partial \mathbf{y}}a^T$$
使用好上述四个结论,对于机器学习尤其是深度学习里的求导问题可以非常快的解决,大家可以试一试。
矩阵向量求导小结
矩阵向量求导在前面我们讨论三种方法,定义法,微分法和链式求导法。在同等情况下,优先考虑链式求导法,尤其是第三节的四个结论。其次选择微分法、在没有好的求导方法的时候使用定义法是最后的保底方案。
基本上大家看了系列里这四篇后对矩阵向量求导就已经很熟悉了,对于机器学习中出现的矩阵向量求导问题已足够。这里还没有讲到的是矩阵对矩阵的求导,还有矩阵对向量,向量对矩阵求导这三种形式,将在第5节简单讨论一下,如果大家只是关注机器学习的优化问题,不涉及其他应用数学问题的,可以不关注。
矩阵对矩阵的求导
前4节我们主要讨论了标量对向量矩阵的求导,以及向量对向量的求导。本文我们就讨论下之前没有涉及到的矩阵对矩阵的求导,还有矩阵对向量,向量对矩阵求导这几种形式的求导方法。
本节所有求导布局以分母布局为准,为了适配矩阵对矩阵的求导,本文向量对向量的求导也以分母布局为准,这和前面的文章不同,需要注意。
本节主要参考了张贤达的《矩阵分析与应用》和长躯鬼侠的矩阵求导术
矩阵对矩阵求导的定义
假设我们有一个$p \times q$的矩阵$F$要对$m \times n$的矩阵$X$求导,那么根据我们第1节求导的定义,矩阵$F$中的$pq$个值要对矩阵$X$中的$mn$个值分别求导,那么求导的结果一共会有$mnpq$个。那么求导的结果如何排列呢?方法有很多种。
最直观可以想到的求导定义有2种:
第一种是矩阵$F$对矩阵$X$中的每个值$X_{ij}$求导,这样对于矩阵$X$每一个位置$(i, j)$求导得到的结果是一个矩阵$\frac{\partial F}{\partial X_{ij}}$,可以理解为矩阵$X$的每个位置都被替换成一个$p \times q$的矩阵,最后我们得到了一个$mp \times nq$的矩阵。
第二种和第一种类似,可以看做矩阵$F$中的每个值$F_{kl}$分别对矩阵$X$求导,这样矩阵$F$每一个位置(k,l)对矩阵$X$求导得到的结果是一个矩阵$\frac{\partial F_{kl}}{\partial X}$, 可以理解为矩阵$F$的每个位置都被替换成一个$m \times n$的矩阵,最后我们得到了一个$mp \times nq$的矩阵。
这两种定义虽然没有什么问题,但是很难用于实际的求导,比如类似我们在第3节中很方便使用的微分法求导。
目前主流的矩阵对矩阵求导定义是对矩阵先做向量化,然后再使用向量对向量的求导。而这里的向量化一般是使用列向量化。也就是说,现在我们的矩阵对矩阵求导可以表示为:$$\frac{\partial F}{\partial X} = \frac{\partial vec(F)}{\partial vec(X)}$$
对于矩阵$F$,列向量化后,$vec(F)$的维度是$pq \times 1$的向量,同样的,$vec(X)$的维度是$mn \times 1$的向量。最终求导的结果,这里我们使用分母布局,得到的是一个$mn \times pq$的矩阵。
矩阵对矩阵求导的微分法
按第一节的向量化的矩阵对矩阵求导有什么好处呢?主要是为了使用类似于前面讲过的微分法求导。回忆之前标量对向量矩阵求导的微分法里,我们有:$$df= tr((\frac{\partial f}{\partial \mathbf{X}})^Td\mathbf{X})$$
这里矩阵对矩阵求导我们有:$$vec(dF) =\frac{\partial vec(F)^T}{\partial vec(X)} vec(dX) = \frac{\partial F^T}{\partial X} vec(dX)$$
和之前标量对矩阵的微分法相比,这里的迹函数被矩阵向量化代替了。
矩阵对矩阵求导的微分法,也有一些法则可以直接使用。主要集中在矩阵向量化后的运算法则,以及向量化和克罗内克积之间的关系。关于矩阵向量化和克罗内克积,具体可以参考张贤达的《矩阵分析与应用》,这里只给出微分法会用到的常见转化性质, 相关证明可以参考张的书。
矩阵向量化的主要运算法则有:
1) 线性性质:$vec(A+B) =vec(A) +vec(B)$
2) 矩阵乘法:$vec(AXB)= (B^T \bigotimes A)vec(X)$,其中$\bigotimes$是克罗内克积。
3) 矩阵转置:$vec(A^T) =K_{mn}vec(A)$,其中$A$是$m \times n$的矩阵,$K_{mn}$是$mn \times mn$的交换矩阵,用于矩阵列向量化和行向量化之间的转换。
4) 逐元素乘法:$vec(A \odot X) = diag(A)vec(X)$, 其中$diag(A)$是$mn \times mn$的对角矩阵,对角线上的元素是矩阵$A$按列向量化后排列出来的。
克罗内克积的主要运算法则有:
1) $(A \bigotimes B)^T = A^T \bigotimes B^T$
2) $vec(ab^T) = b \bigotimes a$
3) $(A \bigotimes B)(C \bigotimes D )=AC \bigotimes BD$
4) $K_{mn} = K_{nm}^T, K_{mn}K_{nm}=I$
使用上面的性质,求出$vec(dF)$关于$ vec(dX)$的表达式,则表达式左边的转置即为我们要求的$\frac{\partial vec(F)}{\partial vec(X)} $,或者说$\frac{\partial F}{\partial X} $
矩阵对矩阵求导实例
下面我们给出一个使用微分法求解矩阵对矩阵求导的实例。
首先我们来看看:$\frac{\partial AXB}{\partial X}$, 假设$A,X,B$都是矩阵,$X$是$m \times n$的矩阵。
首先求$dF$, 和之前第3节的微分法类似,我们有: $$dF =AdXB$$
然后我们两边列向量化(之前的微分法是套上迹函数), 得到:$$vec(dF) = vec(AdXB) = (B^T \bigotimes A)vec(dX)$$
其中,第二个式子使用了上面矩阵向量化的性质2。
这样,我们就得到了求导结果为:$$\frac{\partial AXB}{\partial X} = (B^T \bigotimes A)^T = B \bigotimes A^T$$
利用上面的结果我们也可以得到:$$\frac{\partial AX}{\partial X} = I_n \bigotimes A^T$$$$\frac{\partial XB}{\partial X} = B \bigotimes I_m$$
来个复杂一些的:$\frac{\partial Aexp(BXC)D}{\partial X}$
首先求微分得到:$$dF =A [dexp(BXC)]D = A[exp(BXC) \odot (BdXC)]D $$
两边矩阵向量化,我们有:$$vec(dF) = (D^T \bigotimes A) vec[exp(BXC) \odot (BdXC)] = (D^T \bigotimes A) diag(exp(BXC))vec(BdXC) = (D^T \bigotimes A) diag(exp(BXC))(C^T\bigotimes B)vec(dX) $$
其中第一个等式使用了矩阵向量化性质2,第二个等式使用了矩阵向量化性质4, 第三个等式使用了矩阵向量化性质2。
这样我们最终得到:$$\frac{\partial Aexp(BXC)D}{\partial X} = [(D^T \bigotimes A) diag(exp(BXC))(C^T\bigotimes B)]^T = (C \bigotimes B^T) diag(exp(BXC)) (D\bigotimes A^T )$$
矩阵对矩阵求导小结
由于矩阵对矩阵求导的结果包含克罗内克积,因此和之前我们讲到的其他类型的矩阵求导很不同,在机器学习算法优化中中,我们一般不在推导的时候使用矩阵对矩阵的求导,除非只是做定性的分析。如果遇到矩阵对矩阵的求导不好绕过,一般可以使用4.3最后的几个链式法则公式来避免。
到此机器学习中的矩阵向量求导系列就写完了,希望可以帮到对矩阵求导的推导过程感到迷茫的同学们。
以上所有内容的细节补充请点。
参考资料:
https://www.cnblogs.com/pinard/p/10750718.html
https://www.cnblogs.com/pinard/p/10773942.html
https://www.cnblogs.com/pinard/p/10791506.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号