深度学习之损失函数

机器学习中的所有算法都依靠最小化或最大化函数，我们将其称为“目标函数”。被最小化的函数就被称为“损失函数”。损失函数也能衡量预测模型在预测期望结果方面的性能，如果预测值与实际结果偏离较远，损失函数会得到一个非常大的值。而在一些优化策略的辅助下，我们可以让模型“学会”逐步减少损失函数预测值的误差，从而找到其最小值点。这些优化策略中，最常用的是“梯度下降”。如果把损失函数比作连绵起伏的山峦，那么梯度下降就好比愚公一样尽力削低山脉，让山达到最低点。

损失函数，并非只有一种。根据不同的因素，包括是否存在异常值，所选机器学习算法，梯度下降的的时效，找到预测的置信度和导数的难易度，我们可以选择不同的损失函数。在深度学习之神经网络模型的基本工作原理这篇文章中，损失函数这部分的介绍主要从思路与公式设计的角度展开，对常用的损失函数公式类型进行了粗浅的介绍，本文是关于损失函数的专篇，将换个角度，从其在机器学习和深度学习领域的应用场景来进行分析与归纳。总而言之，没有一个适合所有机器学习算法的损失函数。针对特定问题选择损失函数涉及到许多因素，比如所选机器学习算法的类型、是否易于计算导数以及数据集中异常值所占比例。

损失函数的划分

从学习任务的类型出发，可以从广义上将损失函数分为两大类——回归损失和分类损失。在回归问题处理的则是连续值的预测问题，例如给定房屋面积、房间数量以及房间大小，预测房屋价格。而在分类任务中，我们要从类别值有限的数据集中预测输出，比如给定一个手写数字图像的大数据集，将其分为$0 \sim 9$中的一个。

符号约定

$y$：真实值    $\hat{y}$：预测值    $n$：样本量

回归损失

L2损失

$$MSE = \frac{\sum_{i=1}^{n}(y_i - \hat{y_i})^2}{n}$$

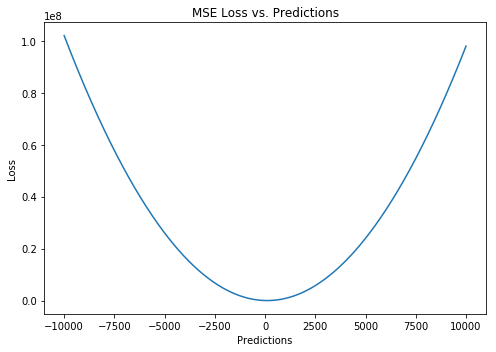
最常见的损失函数，名字也有很多：均方误差（Mean Square Error，MSE）/ 平方损失（Quadratic Loss）。顾名思义，L2损失度量的是预测值和实际观测值间差的平方的均值。它只考虑误差的平均大小，不考虑其方向。但由于经过平方，与真实值偏离较多的预测值会比偏离较少的预测值受到更为严重的惩罚。再加上MSE的数学特性很好，这使得计算梯度变得更容易。

下图是均方误差函数图，其中目标真值为100，预测值范围在-10000到10000之间。均方误差损失（Y轴）在预测值（X轴）= 100处达到最小值。范围为[0, \infty)$。

L1损失

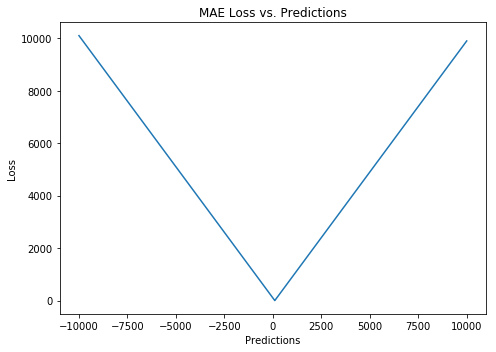
$$MAE = \frac{\sum_{i=1}^{n}|y_i - \hat{y_i}|}{n}$$

L1损失又名平均绝对误差，英文全称Mean Absolute Error。L1损失度量的是预测值和实际观测值之间绝对差之和的平均值。和L2损失一样，这种度量方法也是在不考虑方向的情况下衡量一组预测值的平均误差大小，范围在$[0, \infty)$。但L2的不同之处的是，L1损失需要像线性规划这样更复杂的工具来计算梯度。此外，MAE对异常值更加稳健，因为它不使用平方。

L1 vs. L2

通常来说，使用平方误差更容易解决问题，但使用绝对误差对于异常值更鲁棒。

不管我们什么时候训练机器学习模型，我们的目标都是想找到一个点将损失函数最小化。当然，当预测值正好等于真值时，这两个函数都会达到最小值。

我们来看看两种情况下MAE和均方根误差（RMSE，和MAE相同尺度下MSE的平方根）。在第一种情况下，预测值和真值非常接近，误差在众多观测值中变化很小。在第二种情况下，出现了一个异常观测值，误差就很高。

因为MSE是误差的平方值，那么误差$e$的值在$e > 1$时会增加很多。如果我们的数据中有异常值，$e$的值会非常高，$e^2$会远大于$|e|$。这会让存在MSE误差的模型比存在MAE误差的模型向异常值赋予更多的权重。在上面第2种情况中，存在RMSE误差的模型为了能将该单个异常值最小化会牺牲其它常见情况，这降低模型的整体性能。如果训练数据被异常值破坏的话（也就是我们在训练环境中错误地接收到巨大的不切实际的正/负值，但在测试环境中却没有），MAE会很有用。

试想：如果我们必须为所有的观测值赋予一个预测值，以最小化MSE，那么该预测值应当为所有目标值的平均值。但是如果我们想将MAE最小化，那么预测值应当为所有观测值的中间值。我们知道中间值比起平均值，对异常值有更好的鲁棒性，这样就会让MAE比MSE对异常值更加鲁棒。

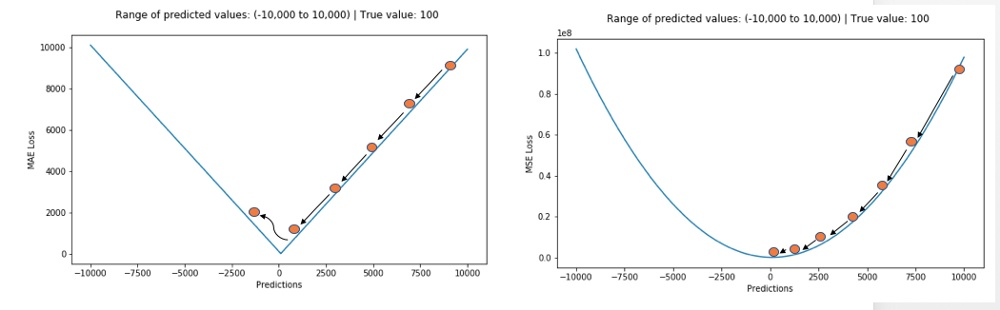
但使用MAE损失（特别是对于神经网络来说）的一个大问题就是，其梯度始终一样，这意味着梯度即便是对于很小的损失值来说，也还会非常大。这对于机器学习可不是件好事。为了修正这一点，我们可以使用动态学习率，它会随着我们越来越接近最小值而逐渐变小。在这种情况下，MSE会表现得很好，即便学习率固定，也会收敛。MSE损失的梯度对于更大的损失值来说非常高，当损失值趋向于0时会逐渐降低，从而让它在模型训练收尾时更加准确（见下图）。

总结

1. 如果异常值表示的反常现象对于业务非常重要，且应当被检测到，那么我们就应当使用MSE。另一方面，如果我们认为异常值仅表示损坏数据而已，那么我们应当选择MAE作为损失函数。
2. L1损失对异常值更鲁棒，但它的导数是不连续的，从而让它无法有效的求解。L2损失对异常值很敏感，但会求出更稳定和更接近的解（通过将导数设为0）。
3. 这两者存在的问题：可能会出现两种损失函数都无法给出理想预测值的情况。例如，如果我们的数据中90%的观测值的目标真值为150， 剩余10%的目标值在0-30之间。那么存在MAE损失的模型可能会预测全部观测值的目标值为150，而忽略了那10%的异常情况，因为它会试图趋向于中间值。在同一种情况下，使用MSE损失的模型会给出大量值范围在0到30之间的预测值，因为它会偏向于异常值。在很多业务情况中，这两种结果都不够理想。

平均偏差误差（Mean Bias Error）

$$MBE = \frac{\sum_{i=1}^{n}(y_i - \hat{y_i})}{n}$$

与其它损失函数相比，这个函数在机器学习领域没有那么常见。它与MAE相似，唯一的区别是这个函数没有用绝对值。用这个函数需要注意的一点是，正负误差可以互相抵消。尽管在实际应用中没那么准确，但它可以确定模型存在正偏差还是负偏差。

Huber Loss

$$L_\delta(y, \hat{y}) = \begin{cases} \frac{1}{2}(y - \hat{y})^2 \quad &for|y - \hat{y}| \leq \delta \\ \delta|y - \hat{y}| - \frac{1}{2}\delta^2 &otherwise \end{cases}$$

又称Smooth Mean Absolute Error，中文名平滑平均绝对误差。相比平方误差损失，Huber损失对于数据中异常值的敏感性要差一些。在值为0时，它也是可微分的。它基本上是绝对值，在误差很小时会变为平方值。误差使其平方值的大小如何取决于一个超参数$\delta$，该参数可以调整。当$\delta \sim 0$时，Huber损失会趋向于MAE；当$\delta \sim \infty$（很大的数字），Huber损失会趋向于MSE。

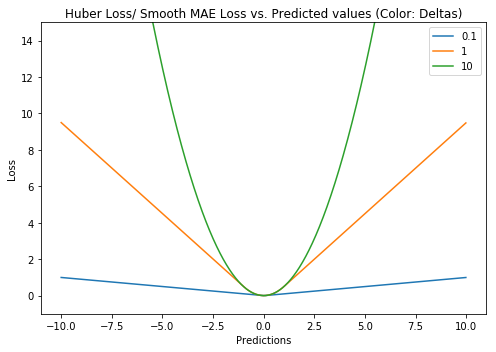
$\delta$的选择非常关键，因为它决定了你如何看待异常值。残差大于$\delta$，就用L1（它对很大的异常值敏感性较差）最小化，而残差小于$\delta$，就用L2“适当地”最小化。

为何使用Huber损失函数？

使用MAE用于训练神经网络的一个大问题就是，它的梯度始终很大，这会导致使用梯度下降训练模型时，在结束时遗漏最小值。对于MSE，梯度会随着损失值接近其最小值而逐渐减少，从而使其更准确。在这些情况下，Huber损失函数真的会非常有帮助，因为它围绕的最小值会减小梯度。而且相比MSE，它对异常值更具鲁棒性。因此，它同时具备MSE和MAE这两种损失函数的优点。不过，Huber损失函数也存在一个问题，我们可能需要训练超参数$\delta$，而且这个过程需要不断迭代。而Huber损失函数的良好表现得益于精心训练的超参数$\delta$。

Log cosh Loss

$$L(y, \hat{y}) = \sum_{i=1}^{n}\log(cosh(\hat{y_i} - y_i))$$

Log-Cosh是应用于回归任务中的另一种损失函数，它比L2损失更平滑。Log-cosh是预测误差的双曲余弦的对数。

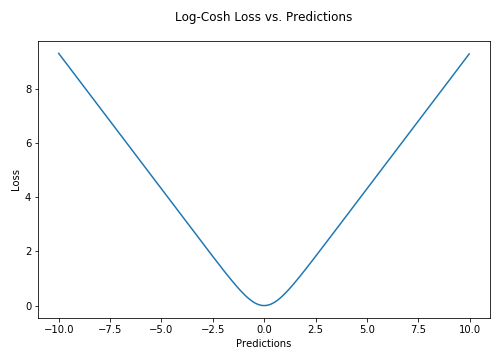
优点

对于较小的$x$值，$\log(cosh(x))$约等于$\frac{x^2}{2}$；对于较大的$x$值，则约等于$abs(x) - log(2)$。这意味着Log-cosh很大程度上工作原理和均方误差很像，但偶尔出现错得离谱的预测时对它影响又不是很大。它具备了Huber损失函数的所有优点，但不像Huber损失，它在所有地方都二次可微。

我们为何需要二阶导数？

很多机器学习模型，比如XGBoost，使用牛顿法来寻找最好结果，因此需要二阶导数（Hessian矩阵）。对于像XGBoost这样的机器学习框架，二次可微函数更为有利。

但Log-cosh也不是完美无缺。如果始终出现非常大的偏离目标的预测值时，它就会遭受梯度问题，因此会导致XGboost的节点不能充分分裂。

Quantile Loss

$$L_\gamma(y, \hat{y}) = \sum_{i=y_i<\hat{y_i}}  ({\gamma-1})|y_i - \hat{y_i}| + \sum_{i=y_i \geq \hat{y_i}}  ({\gamma})|y_i - \hat{y_i}|$$

在大多数现实预测问题中，我们常常很想知道我们的预测值的不确定性。对于很多业务问题而言，相对于知道某个预测点，了解预测值范围能够大幅优化决策过程。如果我们是想预测某个区间而非某个点，那么分位数损失（Quantile Loss）就会非常有用。

通常，最小二乘回归的预测区间基于假设：残差值$y - \hat{y}$在所有独立变量值上的变化保持一致，而违背此假设的回归模型是不可信的。当然我们也不能认为这种情况下用非线性函数或基于树的模型能更好地建模，把拟合线性模型作为基准的理念扔在一边就完了。这时，我们就可以用到Quantile损失和Quantile回归，因为基于Quantile损失的回归能够提供更明智的预测区间，即便是有非常量方差和非正常分布的误差，效果同样不错。

基于Quantile损失的回归能对异方差问题效果良好

Quantile回归 VS 普通最小二乘回归

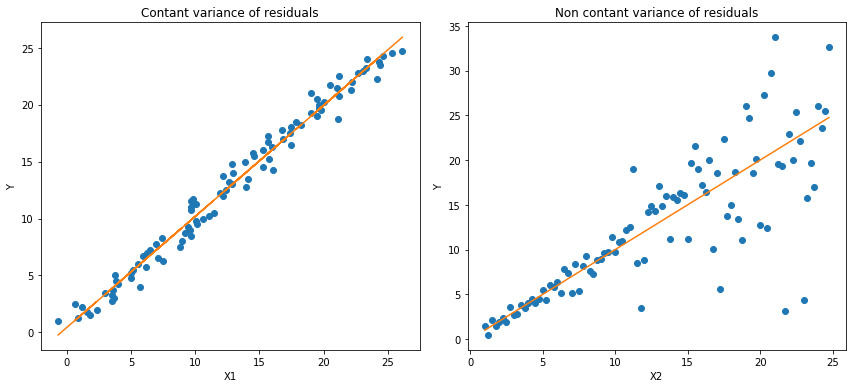
上左为$b/w$ $X1$和$Y$的线性关系，残差的方差为常量方差；上右为$b/w$ $X2$和$Y$的线性关系，$Y$的方差增加2倍。下边两幅图中的橙色直线表示两种情况的OLS预估。我们无法得到取值的区间范围，这时候就需要分位数损失函数来提供。

理解 Quantile 损失函数

基于Quantile的回归模型目的是根据预测变量的特定值，预测反应变量的条件分位数。Quantile损失实际上就是MAE的延伸（当分位数为第50个百分位数时，它就是MAE）。其理念就是根据我们是否想增加正误差或负误差的分量选择合适的分位数值。损失函数会根据所选分位数（$\gamma$）的值，为估计过高或估计不足做出不同的处罚。例如，$\gamma = 0.25$的Quantile损失函数会向估计过高做出更多的惩罚，将预测值保持在略微低于平均值的状态。$\gamma$就是所需的分位数，值范围在$0$和$1$之间。

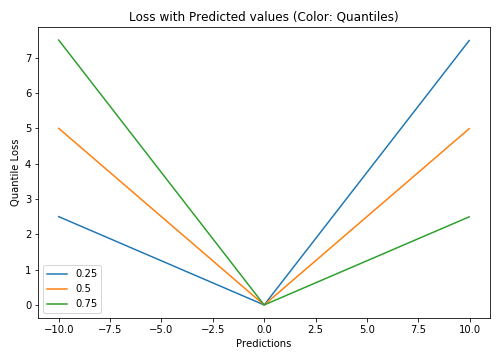
我们也能用该损失函数计算神经网络或基于树的模型的预测区间。下面是用Sklearn实现梯度渐进回归树模型的示例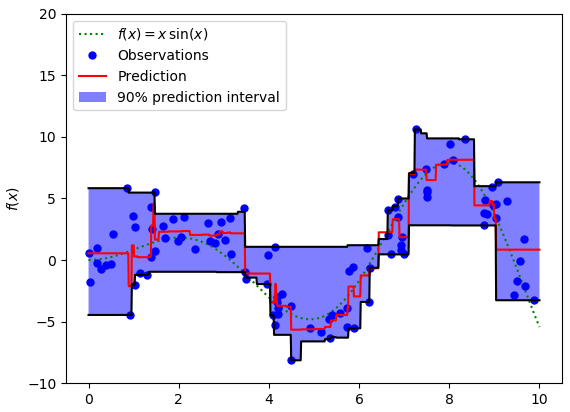

上图展示了用Sklearn和Quantile损失函数计算出的梯度渐进回归树中90%的预测区间。以$\gamma = 0.95$构建上界，以$\gamma =0.05$构建下界。

比较研究

在文章《Gradient Boosting Machines, a Tutorial》中，很好的比较了这几种损失函数。为了展示以上所有损失函数的属性，文章作者模拟了一个取样于sinc(x)函数的数据集，以及两个人工模拟噪声数据集：高斯噪声分量$\epsilon \sim N(0, \sigma^2)$，以及脉冲噪声分量$\xi \sim Bern(p)$。作者添加了脉冲噪声项来说明鲁棒影响。下图是用不同损失函数拟合GBM回归模型的结果。

图中依次为（A）MSE损失函数（B）MAE损失函数（C）Huber损失函数（D）Quantile损失函数（E）原始sinc(x) 函数（F）拟合了MSE和MAE损失的平滑GBM（G）拟合了huber损失为$\delta = \{4, 2, 1\}$的平滑GBM（H）拟合了Quantile损失为$\alpha = \{0.5, 0.1, 0.9\}$的平滑GBM。

从以上模拟中我们可以观察到：

• 有MAE损失的模型预测值受脉冲噪声的影响较小，而有MSE损失的模型预测值由于噪声数据导致的偏差，则出现轻微偏差。
• 有Huber损失的模型预测值对于所选超参数的值敏感度较小。
• Quantile损失在对应置信度水平上做出了很好的预测。

最后把以上所有损失函数绘制在一张图中：

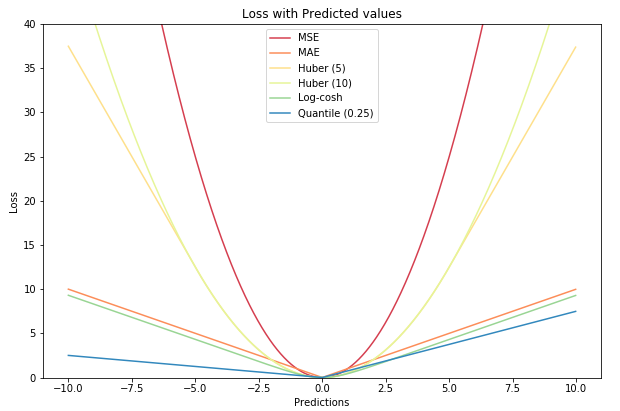
分类损失

逻辑回归是最常见的分类模型，具有如下形式：$$p(x;w,b) = \sigma(w^Tx + b) = \frac{1}{1 + \mathrm{e}^{-w^Tx+b}}$$

 

其中 $p(x;w,b)$表示预测类别为1的概率，记 $\theta = (b, w)$。

对于二分类问题，$y \in \{−1,+1\}，损失函数常表示为关于$yf(x)$的单调递减形式。如下图

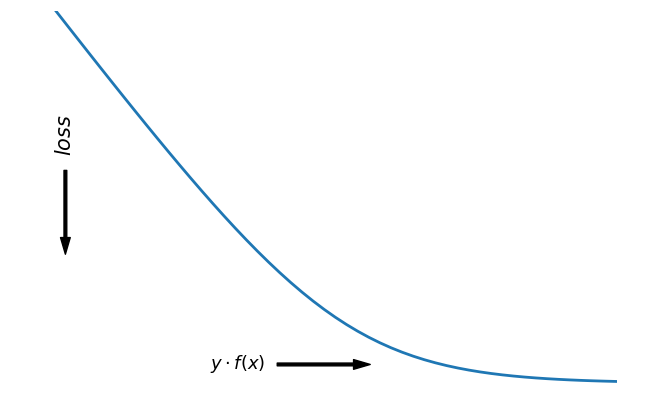
其中$yf(x)$被称为margin，其作用类似于回归问题中的残差$y - \hat{y}$。此处，$f(x)$即$\hat{y}$。

二分类问题中的分类规则通常为$$sign(f(x)) = \begin{cases} +1 \quad if\  yf(x) \geq 0 \\ -1 \quad if\ yf(x) < 0 \end{cases}$$ 

可以看到如果$yf(x) \geq 0$，则样本分类正确，$yf(x) < 0$则分类错误，而相应的分类决策边界即为$f(x) = 0$。所以最小化损失函数也可以看作是最大化margin的过程，任何合格的分类损失函数都应该对$margin < 0$的样本施以较大的惩罚。

0-1损失 (Zero-one loss)

$$L(y, f(x)) =  \begin{cases} 0\quad if\quad yf(x) \geq 0 \\ 1\quad if\quad yf(x) < 0 \end{cases}$$

0-1损失对每个错分类点都施以相同的惩罚，这样那些“错的离谱“ (即$margin \to -\infty$)的点并不会收到大的关注，这在直觉上不是很合适。另外0-1损失不连续、非凸，优化困难，因而常使用其他的代理损失函数进行优化。

Logistic Loss

$$L(y,f(x)) = \log(1 + \mathrm{e}^{-yf(x)})$$

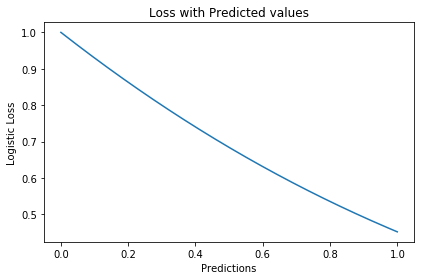
logistic Loss为Logistic Regression中使用的损失函数，下面做一下简单证明：

Logistic Regression中使用了Sigmoid函数表示预测概率：$$g(f(x)) = P(y=1|x) = \frac{1}{1 + \mathrm{e}^{-f(x)}}$$

而$$P(y = -1|x) = 1 - P(y = 1|x) = 1 - \frac{1}{1 + \mathrm{e}^{-f(x)}} = \frac{1}{1 + \mathrm{e}^{f(x)}} = g(-f(x))$$

因此利用$y \in \{-1, +1\}$，可写为$P(y|x) = \frac{1}{1 + \mathrm{e}^{-yf'(x)}}$。此为一个概率模型，利用极大似然的思想：

$$\max(\prod_{i=1}^{m}P(y_i|x_i)) = \max(\prod_{i=1}^{m}\frac{1}{1 + \mathrm{e}^{-y_if(x_i)}})$$

两边取对数，又因为是求损失函数，则将极大转为极小：$$\max(\sum_{i=1}^{m}\log P(y_i|x_i)) = -\min(\sum_{i=1}^{m}\log(\frac{1}{1 + \mathrm{e}^{-y_if(x_i)}})) = \min(\sum_{i=1}^{m}\log(1 + \mathrm{e}^{-y_if(x_i)}))$$

这样就得到了logistic loss。

如果定义$t = \frac{y + 1}{2} \in \{0, 1\}$，则极大似然法可写为：

$$\prod_{i=1}^{m}(P(t_i = 1|x_i))^{t_i}((1 - P(t_i = 1|x))^{1 - t_i}$$

取对数，并转为极小得：$$\sum_{i=1}^{m}\{-t_i\log P(t_i = 1|x_i) - (1 - t_i)\log(1 - P(t_i = 1|x_i))\}$$

上式被称为交叉熵损失（Cross entropy loss），可以看到在二分类问题中logistic loss和交叉熵损失是等价的，二者区别只是标签$y$的定义不同。

【以上证明是在概率函数确定为Sigmoid的基础上所做的推导，对于更普遍的直接用概率$p$表示而进行的推导，详见下一节交叉熵损失。】

交叉熵损失（Cross Entropy Loss）

$$Cross\ Entropy\ Loss = -(y_i\log(\hat{y_i}) + (1 - y_i)\log(1 - \hat{y_i}))$$

先介绍一个概念——KL距离，是Kullback-Leibler散度（Kullback-Leibler Divergence）的简称，也叫做相对熵（Relative Entropy）。它衡量的是相同事件空间里的两个概率分布的差异情况。其物理意义是：在相同事件空间里，概率分布$P(x)$对应的每个事件，若用概率分布$Q(x)$编码时，平均每个基本事件（符号）编码长度增加了多少比特。我们用$D(P||Q)$表示KL距离，计算公式如下：$$D(P||Q) = \sum_{x \in X}P(x)\log \frac{P(x)}{Q(x)} = -\sum_{x \in X}P(x)\log Q(x) - H(P)$$

其中$P$称为真实分布，$Q$称为拟合分布，$H(P)$是$P$的熵，为常数。因此$-\sum_{x \in X}P(x)\log Q(x)$度量了$P$和$Q$两个分布之间的距离，叫作交叉熵损失。

【有关熵的相关知识在信息，信息量与信息熵这篇有专门的介绍，这里就不展开详谈了。】

在二分类问题中，数据的真实分布为$(y, 1 - y)$，预测分布为$(P(x;\theta), 1 - P(x;\theta))$，因此交叉熵损失为$$-(y_i\log P(x;\theta) + (1 - y_i)\log(1 - P(x;\theta)))$$。

注意，当实际标签为 1(y(i)=1) 时，函数的后半部分消失，而当实际标签是为 0(y(i=0)) 时，函数的前半部分消失。简言之，我们只是把对真实值类别的实际预测概率的对数相乘。还有重要的一点是，交叉熵损失会重重惩罚那些置信度高但是错误的预测值。

负对数似然损失（Negative Log Likelihood）

上一节推导证明了交叉熵损失在某些条件下等价于负对数似然损失。

从极大似然的角度出发，我们希望极大化如下似然函数：$$l(\theta) = \log \prod_{i=1}^{n}P_{y_i}(x_i;\theta) = \sum_{i=1}{n}\log P_{y_i}(x_i;\theta)$$

其中$P_k(x;\theta) = P(y=k|x;\theta)$。当$y=1$时，$P_k(x;\theta) = P(x;\theta)$；当$y=0$时，$P_k(x;\theta) = 1 -P(x;\theta)$。于是，$$\log P_Y(x;\theta) = y\log P(x;\theta) + (1 - y)\log(1 - P(x;\theta))$$

最大化上式等价于极小化下式$$\sum_{i=1}^{m}\{-t_i\log P(t_i = 1|x_i) - (1 - t_i)\log(1 - P(t_i = 1|x_i))\}$$

该式被称为负对数似然损失，与上一节的推导结果一模一样。

交叉熵与Softmax

Softmax分类器使用的即为交叉熵损失函数，Binary Cross Entropy Loss为二分类交叉熵损失，Categorical Crossentropy为多分类交叉熵损失，当使用多分类交叉熵损失函数时，标签应该为多分类模式，即使用one-hot编码的向量。

实际上，Softmax是由Logistic Regression模型（用于二分类）推广得到的多项Logistic Regression模型（用于多分类）。具体可以参考李航大神的《统计学方法》第六章，这里给一个大致的过程：

逻辑回归的$P(Y=y|x)$表达式如下$$P(Y=y|x) = \begin{cases} h_{\theta}(x) = g(f(x)) = \frac{1}{1+exp\{-f(x)\}} \quad &y=1 \\ 1 - h_{\theta}(x) = 1 - g(f(x)) = \frac{1}{1+exp\{f(x)\}} &y=0\end{cases}$$

将它代入上式，通过推导可以得到logistic的损失函数表达式，如下$$L(y, P(Y=y|x)) = \begin{cases} \log(1+exp\{-f(x)\}) \quad y=1 \\ \log(1+exp\{f(x)\}) \quad y=0 \end{cases}$$

逻辑回归最后得到的式子如下$$J(\theta) = -\frac{1}{m}[\sum_{i=1}^{m}y^(i)\log h_{\theta}(x^{(i)}) + (1-y^{(i)})\log (1 - h_{\theta}(x^{(i)}))]$$

篇幅有限，有关交叉熵损失函数与softmax更多的理论与实践内容推荐飞鱼Talk的这篇：损失函数 - 交叉熵损失函数

Hinge Loss

$$L(y) = \max(1-y\hat{y})$$

Hinge loss，中文名铰链损失，也被翻译为“合页损失“”。在机器学习中常用于"最大间隔（maximum-margin）"的分类任务中，如支持向量机SVM。尽管不可微，但它是一个凸函数，因此可以轻而易举地使用机器学习领域中常用的凸优化器。

数学表达式中的$\hat{y}$是预测输出，通常都是软结果（即输出不是0，1这种，可能是0.87），$y$表示正确的类别。

• 如果$\hat{y}y < 1$，则损失为：$1 - \hat{y}y$
• 如果$\hat{y}y \geq 1$，则损失为：$0$

Hinge loss使得$hat{y}y > 1$的样本损失皆为0，由此带来了稀疏解，使得SVM仅通过少量的支持向量就能确定最终超平面。

其函数图像如下，与0-1损失对比：

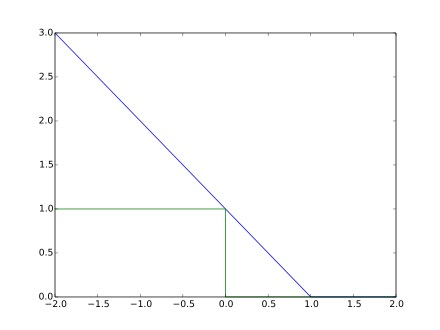
优化

以支持向量机为例，其模型为：$\hat{y} = w \cdot x$，如果用Hinge损失，其求导结果如下：

$$\frac{\partial L}{\partial w_i} = \begin{cases} -y\cdot x_i &if\quad \hat{y}y < 1 \\ 0 \quad&otherwise \end{cases}$$

变种

实际应用中，一方面很多时候我们的y的值域并不是$[-1,1]$，比如我们可能更希望$y$更接近于一个概率，即其值域最好是$[0,1]$。另一方面，很多时候我们希望训练的是两个样本之间的相似关系，而非样本的整体分类，所以很多时候我们会用下面的公式：

$$l(y, y') = \max(0, m - y + y')$$

其中，$y$是正样本的得分，$y’$是负样本的得分，$m$是margin（自己选一个数）。

即我们希望正样本分数越高越好，负样本分数越低越好，但二者得分之差最多到$m$就足够了，差距增大并不会有任何奖励。

比如，我们想训练词向量，我们希望经常同时出现的词，他们的向量内积越大越好；不经常同时出现的词，他们的向量内积越小越好。则我们的Hinge loss function可以是：$$l(w,w+,w-) = \max(0, 1 - w^T\cdot w +\ +w^T\cdot w-)$$

其中，$w$是当前正在处理的词， $w+$是$w$在文中前3个词和后3个词中的某一个词， $w-$是随机选的一个词。

Exponential Loss

$$L(y,f(x)) = \mathrm{e}^{-yf(x)}$$

学过Adaboost算法的人都知道，它是前向分步加法算法的特例，是一个加和模型，其损失函数就是指数损失（Exponential Loss）。在Adaboost中，经过$m$次迭代之后，可以得到$f_m(x)$：$f_m(x) = f_{m-1}(x)+\alpha_{m}G_m(x)$

Adaboost每次迭代时的目的是为了找到最小化下列式子时的参数$\alpha$和$G$：$$arg\min_{\alpha,G} = \sum_{i=1}^{N}exp[-y_i(f_{m-1}(x_i) + \alpha G(x_i))]$$

对比指数损失函数可以看出，Adaboost的目标式子就是指数损失，在给定$n$个样本的情况下，Adaboost的损失函数为：$$L(y,f(x)) =\frac{1}{n}\sum_{i=1}^{n}exp[-y_if(x_i)]$$

然而其和squared loss一样，对异常点敏感，不够robust。

忽略模型的具体形式，在指数损失下，我们的优化目标为$$\min_{f(x)}E_xE_{Y|x}(\mathrm{e}^{-Yf(x)})$$

最优解为（公式5）$$f^{*}(x) = arg\min_{f(x)}E_xE_{Y|x}(\mathrm{e}^{-Yf(x)}) = \frac{1}{2}\log \frac{Pr(Y=1|x)}{Pr(Y=-1|x)}$$

$f^{*}(x)$估计的是对数几率的一半。当$Pr(Y=1|x) > Pr(Y=-1)$时， $f^{*}(x)$的符号为正，反之为负。于是$sign(f^{*}(x))$作为预测值可达贝叶斯最优。这说明了指数函数作为损失函数的合理性。当$f(x)$为线性函数时，这就是Logistic Regression。

可以看到，损失函数决定了模型的最优值是什么，模型的形式决定了在哪个函数空间去逼近这个最优值。

从上式得到，$$P(x) = Pr(Y=1|x) = \frac{1}{1+\mathrm{e}^{-2f(x)}}$$

令$Y' = (Y + 1)/2 \in \{0, 1\}$，那么负对数似然损失为$$\begin{align}l(Y, P(x)) &= -Y'\log P(x) - (1 - Y')\log(1 - P(x)) \\ &=\log(1+\mathrm{e}^{-2Yf(x)}) \end{align}$$

其最优解（公式7）为$$f(x) = \frac{1}{2}\log\frac{P(y=1|x)}{P(y=-1|x)}$$

因此，在期望意义下，指数损失和负对数似然损失对应了相同的解公式5和7。

但对于样本损失来说，负对数似然损失有更好的鲁棒性。举个例子就好理解了，估计正态分布的均值，平均数（ L2损失的最优值）和中位数（ L1损失的最优值）都是无偏估计，但中位数对于异常值的波动性更小。因为L2对偏离较远的点惩罚较重（平方），L1对偏离较远的点惩罚较轻（线性）。同样的，指数损失对于向左偏离较远的$Yf(x)$惩罚也太重了（指数），负对数似然是线性惩罚。

Focal Loss

$$L_{FL}(y) = \begin{cases} -\alpha(1-y')^{\gamma}\log y' \quad &y=1 \\ -(1-alpha)y'^{\gamma}\log(1-y') &y=0\end{cases}$$

Focal Loss来自ICCV2017 RBG和Kaiming大神的新作《Focal Loss for Dense Object Detection》。论文详解推荐这篇Focal loss论文详解，介于篇幅，这里只做简单介绍。

Focal loss主要是为了解决one-stage目标检测中正负样本比例严重失衡的问题。该损失函数降低了大量简单负样本在训练中所占的权重，也可理解为一种困难样本挖掘。它是在交叉熵损失函数基础上进行的修改，首先回顾二分类交叉熵损失：$$L_{CE} = -y\log y' - (1-y)\log(1-y') = \begin{cases} -\log y' &y=1 \\ -\log(1-y') &y=0 \end{cases}$$

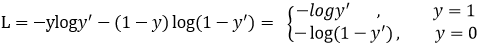
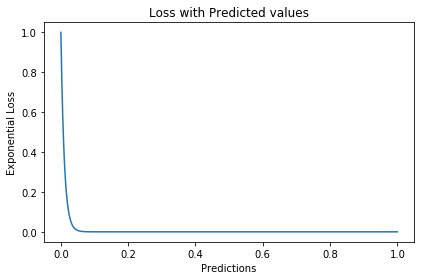
$y'$是经过激活函数的输出，所以在0-1之间。可见普通的交叉熵对于正样本而言，输出概率越大损失越小。对于负样本而言，输出概率越小则损失越小。此时的损失函数在大量简单样本的迭代过程中比较缓慢且可能无法优化至最优。那么Focal loss是怎么改进的呢？$$L_{FL} = \begin{cases} -(1-y')^{\gamma}\log y' &y=1 \\ -y'^{\gamma}\log(1-y') &y=0\end{cases}$$

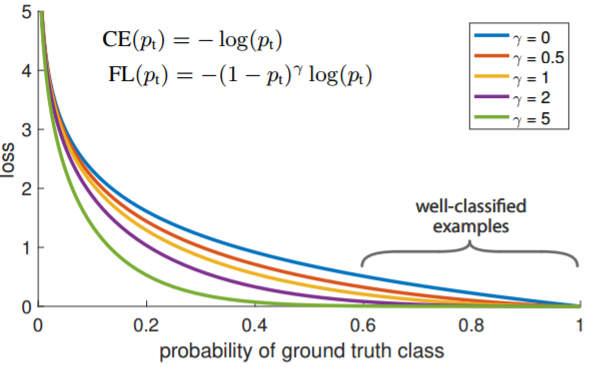
首先在原有的基础上加了一个因子，其中$\gamma > 0$使得减少易分类样本的损失。使得更关注于困难的、错分的样本。

例如$\gamma$为$2$，对于正类样本而言，预测结果为$0.95$肯定是简单样本，所以$(1-0.95)$的$\gamma$次方就会很小，这时损失函数值就变得更小。而预测概率为$0.3$的样本其损失相对很大。对于负类样本而言同样，预测$0.1$的结果应当远比预测$0.7$的样本损失值要小得多。对于预测概率为$0.5$时，损失只减少了$0.25$倍，所以更加关注于这种难以区分的样本。这样减少了简单样本的影响，大量预测概率很小的样本叠加起来后的效应才可能比较有效。

此外，加入平衡因子$\alpha$，用来平衡正负样本本身的比例不均：文中$\alpha$取$0.25$，即正样本要比负样本占比小，这是因为负例易分。

$$L_{FL} = \begin{cases} -\alpha(1-y')^{\gamma}\log y' &y=1 \\ -(1-\alpha)y'^{\gamma}\log(1-y') &y=0 \end{cases}$$

只添加$\alpha$虽然可以平衡正负样本的重要性，但是无法解决简单与困难样本的问题。

$\gamma$调节简单样本权重降低的速率，当$\gamma$为$0$时即为交叉熵损失函数，当$\gamma$增加时，调整因子的影响也在增加。实验发现$\gamma$为$2$是最优。

总结

作者认为one-stage和two-stage的表现差异主要原因是大量前景背景类别不平衡导致。作者设计了一个简单密集型网络RetinaNet来训练在保证速度的同时达到了精度最优。在双阶段算法中，在候选框阶段，通过得分和nms筛选过滤掉了大量的负样本，然后在分类回归阶段又固定了正负样本比例，或者通过OHEM在线困难挖掘使得前景和背景相对平衡。而one-stage阶段需要产生约100k的候选位置，虽然有类似的采样，但是训练仍然被大量负样本所主导。

补充解答

为什么平方损失函数不适用分类问题？

直观上，对特定的分类问题，平方差的损失有上限(所有标签都错，损失值是一个有效值)，但交叉熵则可以用整个非负域来反映优化程度的程度。

从本质上看，平方差的意义和交叉熵的意义不一样。概率理解上，平方损失函数意味着模型的输出是以预测值为均值的高斯分布，损失函数是在这个预测分布下真实值的似然度，Softmax损失意味着真实标签的似然度。

分类问题中的标签，是没有连续的概念的。one-hot作为标签的一种表达方式，每个标签之间的距离也是没有实际意义的，所以预测值和标签两个向量之间的平方差这个值不能反应分类这个问题的优化程度。

还有个原因应该是Softmax带来的梯度消失吧。预测值离标签越远，有可能的梯度越小。李龙说的non-convex问题，应该是一种体现形式。

能不能设计一个分类模型，当使用平方损失时，损失函数关于参数是凸函数？

一个简单而不成熟的想法是，把这个问题当成回归问题，$f(x) = w^T + b$。当$f(x) > 0$时，预测值为$1$。当$f(x) < 0$时，预测值为$-1$。损失函数是凸函数，如下图：

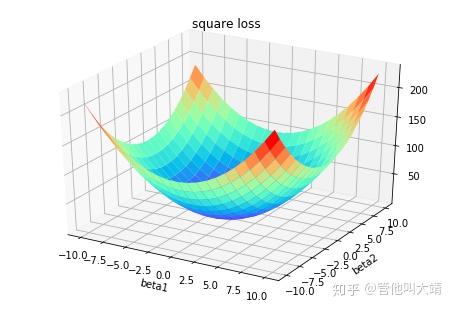
但这个平方损失+线性模型可以说是非常糟糕了，鲁棒性特别差！如果一个点碰巧标记错了又离最优的boundary特别远，很可能导致友军全军覆没。

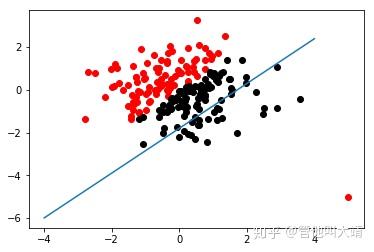
增强鲁棒性的一个直接的想法是，对模型进行截断或者对损失函数进行截断。

对模型截断：$$f(x;w,b) = \begin{cases} 1 &if\quad w_Tx + b > 1 \\ -1 &if\quad w^Tx + b < -1 \\ w^Tx + b &else \end{cases}$$

对损失函数截断：$$loss(y;f(x)) = \begin{cases} 1&if\quad  loss(y;f(x)) > 1 \\ -1&if\quad loss(y;f(x)) < -1 \\ loss(y;f(x)) &else \end{cases}$$

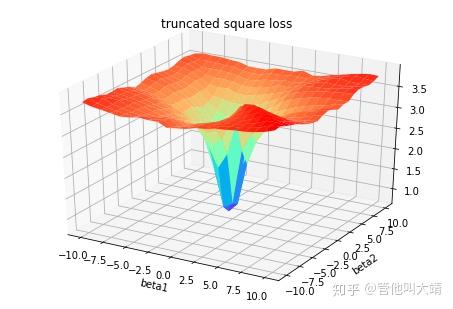
线性模型+截断平方损失

截断线性模型+平方损失

随着深度学习推动了一系列非凸优化算法的研究和应用，在工程中大家并不太关心损失函数，或者说损失函数的选择比较少，而是将重心放在如何去设计模型的结构。神经网络中有一个例子展现了优雅的损失函数是如何发挥作用的，那就是孪生网络中的Contrastive Loss。

（整理自网络）

参考资料：

https://nbviewer.jupyter.org/github/groverpr/Machine-Learning/blob/master/notebooks/05_Loss_Functions.ipynb

https://www.jiqizhixin.com/articles/091202

https://zhuanlan.zhihu.com/p/39239829

https://zhuanlan.zhihu.com/p/35708936

https://zhuanlan.zhihu.com/p/74073096

https://www.zhihu.com/question/319865092

https://blog.csdn.net/zhangjunp3/article/details/80467350

https://www.cnblogs.com/massquantity/p/8964029.html

https://www.pianshen.com/article/3162136463/

https://www.cnblogs.com/king-lps/p/9497836.html