桶排序（Bucket Sort）

标签

稳定排序、非原地排序、非比较排序

基本思想

桶排序也是分配排序的一种，但其是基于比较排序的，这也是与基数排序最大的区别所在。

桶排序也是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。

桶排序算法想法类似于散列表。首先要假设待排序的元素输入符合某种均匀分布，例如数据均匀分布在[ 0,1）区间上，则可将此区间划分为10个小区间，称为桶，对散布到同一个桶中的元素再排序（可使用别的排序算法或是以递归方式继续）。

要求：待排序数长度一致。

基数排序 vs 计数排序 vs 桶排序

这三种排序算法都利用了桶的概念，但对桶的使用方法上有明显差异：

• 基数排序： 根据键值的每位数字来分配桶。
• 计数排序： 每个桶只存储单一键值。
• 桶排序： 每个桶存储一定范围的数值。

算法描述

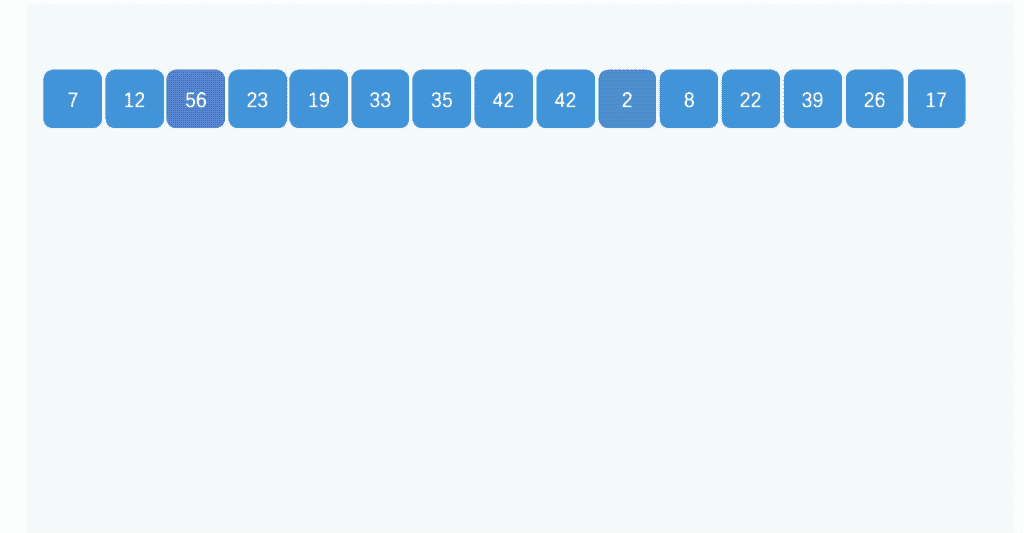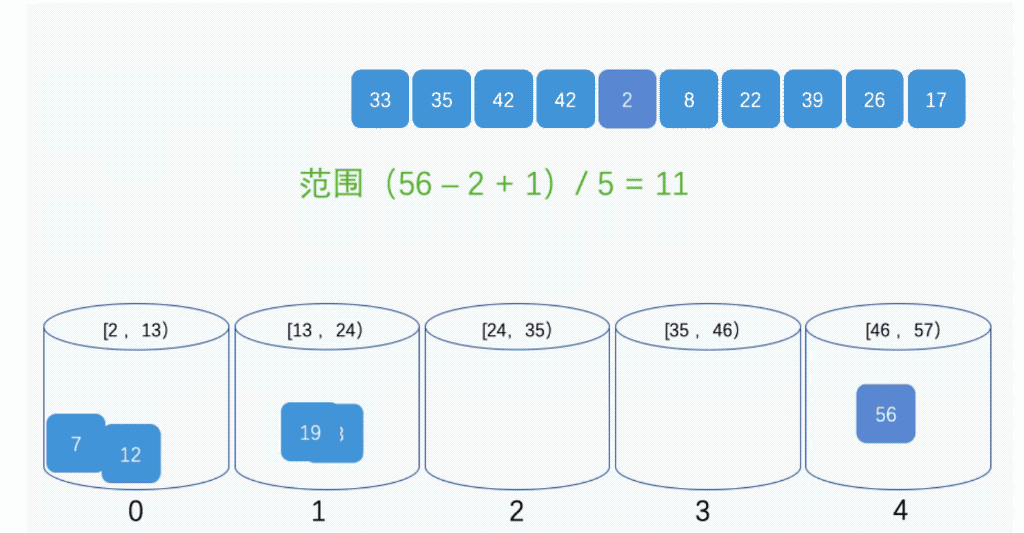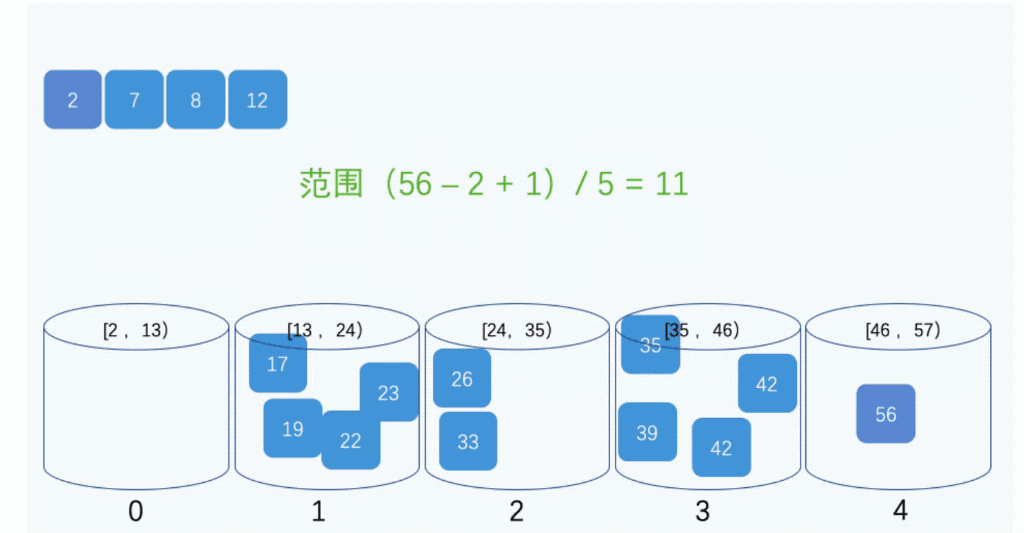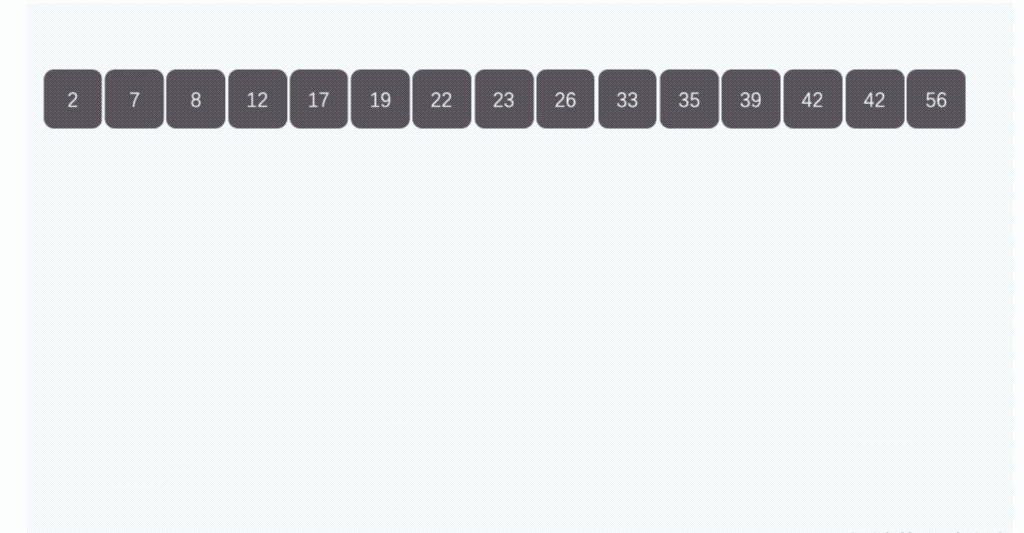
• 步骤1：人为设置一个BucketSize，作为每个桶所能放置多少个不同数值（例如当BucketSize==5时，该桶可以存放｛1,2,3,4,5｝这几种数字，但是容量不限，即可以存放100个3）；
• 步骤2：遍历输入数据，并且把数据一个一个放到对应的桶里去；
• 步骤3：对每个不是空的桶进行排序，可以使用其它排序方法，也可以递归使用桶排序；
• 步骤4：从不是空的桶里把排好序的数据拼接起来。 
  
  注意，如果递归使用桶排序为各个桶排序，则当桶数量为1时要手动减小BucketSize增加下一循环桶的数量，否则会陷入死循环，导致内存溢出。

动图演示

时间复杂度

对$n$个关键字进行桶排序的时间复杂度分为两个部分： 
(1) 循环计算每个关键字的桶映射函数，这个时间复杂度是O(n)。

(2) 利用先进的比较排序算法对每个桶内的所有数据进行排序，对于n个待排数据，m个桶，平均每个桶[n / m]个数据，则桶内排序的时间复杂度为$\sum{i = 1}^{m} O(n_i ∗ log n_i) = O(n * log nm)$。其中$n_i$为第$i$个桶的数据量。

因此，桶排序的时间复杂度，取决与对各个桶之间数据进行排序的时间复杂度，因为其它部分的时间复杂度都为$O(n)$。很显然，桶划分的越小，各个桶之间的数据越少，排序所用的时间也会越少。但相应的空间消耗就会增大。平均时间复杂度为线性的$O(n + k)$，$k$为桶内排序所花费的时间。当每个桶只有一个数，则最好的时间复杂度为：$O(n)$。

最好情况：$O(n)$

最坏情况：$O(n + k)$

平均情况：$O(n + k)$

空间复杂度

额外的空间开销为桶的个数 * 每个桶所占内存空间。

算法示例

 

参考资料：

https://blog.csdn.net/coolwriter/article/details/78732728

https://blog.csdn.net/weixin_41190227/article/details/86600821

https://www.cnblogs.com/itsharehome/p/11058010.html