图的搜索算法之迷宫问题和棋盘马走日问题
算法背景
迷宫问题和棋盘马走日问题都是搜索问题(找路径),一般采用DFS和BFS两种搜索算法都可以,如果要求是最短路径,则一般BFS解题,DFS则需要记录所有的可能路径,找到最短的那条。一般来说,迷宫问题的前进方向为四个(上下左右),障碍物直接用1和0来判断。而马走日则有特殊的障碍物判断规则,前进方向也扩展为了八个(上下左右和四个斜角)。下面就用算法实例来讲解这类问题的一般解法。
迷宫问题(带障碍物)
例题一:(求通路)
输入:一个二维矩阵,表示迷宫(0表示通道,1表示围墙)。
maze = { {1,1,1,1,1,1,1,1,1,1], [1,0,0,1,0,0,0,1,0,1], [1,0,0,1,0,0,0,1,0,1], [1,0,0,0,0,1,1,0,0,1], [1,0,1,1,1,0,0,0,0,1], [1,0,0,0,1,0,0,0,0,1], [1,0,1,0,0,0,1,0,0,1], [1,0,1,1,1,0,1,1,0,1], [1,1,0,0,0,0,0,0,0,1], {1,1,1,1,1,1,1,1,1,1} }
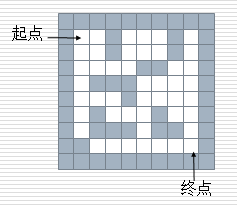
输出:一条走出迷宫的路径。
解题方法有两种:栈和队列。
栈(DFS)
解题思路
- 在一个迷宫节点(x,y)上,可以进行四个方向的探查:maze[x-1][y], maze[x+1][y], maze[x][y-1], maze[x][y+1]
- 思路:从一个节点开始,任意找下一个能走的点,当找不到能走的点时,退回上一个点寻找是否有其他方向的点。
- 方法:创建一个空栈,首先将入口位置进栈。当栈不空时循环:获取栈顶元素,寻找下一个可走的相邻方块,如果找不到可走的相邻方块,说明当前位置是死胡同,进行回溯(就是讲当前位置出栈,看前面的点是否还有别的出路)
代码实现(C)
#include <stdio.h> #include <stdlib.h> #include <string.h> typedef struct Node { int x, y; } Node; typedef struct Stack { Node **data; int top_index, length; } Stack; int direct[4][2] = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}}; int maze[10][10] = { {1,1,1,1,1,1,1,1,1,1}, {1,0,0,1,0,0,0,1,0,1}, {1,0,0,1,0,0,0,1,0,1}, {1,0,0,0,0,1,1,0,0,1}, {1,0,1,1,1,0,0,0,0,1}, {1,0,0,0,1,0,0,0,0,1}, {1,0,1,0,0,0,1,0,0,1}, {1,0,1,1,1,0,1,1,0,1}, {1,1,0,0,0,0,0,0,0,1}, {1,1,1,1,1,1,1,1,1,1} }; void init_node(Node *node, int x, int y) { node->x = x; node->y = y; return; } void init_stack(Stack *s, int size) { s->length = size; s->data = (Node **)malloc(sizeof(Node *) * size); s->top_index = -1; return; } void push(Stack *s, Node *node) { if (s->top_index >= s->length) { return; } s->top_index++; s->data[s->top_index] = node; return; } int empty(Stack *s) { if (s->top_index < 0) { return 1; } else { return 0; } } Node *top(Stack *s) { return s->data[s->top_index]; } void pop(Stack *s) { if (empty(s)) { return; } else { s->top_index--; return; } } void clear_stack(Stack *s) { free(s->data); free(s); } void output(Stack *s) { for (int i =0; i <= s->top_index; ++i) { i == 0 || printf("=>"); printf("(%d, %d)", s->data[i]->x, s->data[i]->y); } printf("\n"); return; } int check(int x, int y) { if (x >=0 && x < 10 && y >=0 && y < 10) { return 1; } else { return 0; } } void solve_maze(int x0, int y0, int x1, int y1) { Stack *s = (Stack *)malloc(sizeof(Stack)); init_stack(s, 100); Node *start_node = (Node *)malloc(sizeof(Node)); init_node(start_node, x0, y0); push(s, start_node); maze[x0][x1] = -1; int flag; while (!empty(s)) { Node *cur_node = top(s); flag = 0; if (cur_node->x == x1 && cur_node->y == y1) { output(s); printf("Success!\n"); return; } for (int i = 0; i < 4; i++) { if (check(cur_node->x + direct[0][i], cur_node->y + direct[1][i]) && maze[cur_node->x + direct[0][i]][cur_node->y + direct[1][i]] == 0) { Node *tmp = (Node *)malloc(sizeof(Node)); init_node(tmp,cur_node->x + direct[0][i], cur_node->y + direct[1][i]); push(s, tmp); maze[cur_node->x + direct[0][i]][cur_node->y + direct[1][i]] = -1; output(s); flag = 1; break; } } if (flag == 0) { pop(s); } } printf("Failed!\n"); return; } int main() { int x0, y0, x1, y1; scanf("%d%d%d%d", &x0, &y0, &x1, &y1); solve_maze(x0, y0, x1, y1); return 0; }
最后生成的是深度优先搜索树,每个结点只访问一次,注意在入栈时要将maze的信息置为-1,表示已访问,不然会陷入死循环!!
队列(BFS)
解题思路
- 思路:从一个节点开始,寻找所有下面能继续走的点。继续寻找,直到找到出口。
- 方法:创建一个空队列,将起点位置进队。在队列不为空时循环:出队一次。如果当前位置为出口,则结束算法;否则找出当前方块的4个相邻方块中可走的方块,全部进队。
代码实现(C)
#include <stdio.h> #include <stdlib.h> #include <string.h> typedef struct Node { int x, y, pre; } Node; typedef struct Queue { Node **data; int head, tail, length; } Queue; int direct[4][2] = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}}; int maze[10][10] = { {1,1,1,1,1,1,1,1,1,1}, {1,0,0,1,0,0,0,1,0,1}, {1,0,0,1,0,0,0,1,0,1}, {1,0,0,0,0,1,1,0,0,1}, {1,0,1,1,1,0,0,0,0,1}, {1,0,0,0,1,0,0,0,0,1}, {1,0,1,0,0,0,1,0,0,1}, {1,0,1,1,1,0,1,1,0,1}, {1,1,0,0,0,0,0,0,0,1}, {1,1,1,1,1,1,1,1,1,1} }; void init_node(Node *node, int x, int y, int pre) { node->x = x; node->y = y; node->pre = pre; return; } void init_queue(Queue *q, int size) { q->length = size; q->data = (Node **)malloc(sizeof(Node *) * size); q->head = 0; q->tail = -1; return; } void push(Queue *q, Node *node) { if (q->tail + 1 >= q->length) { return; } q->tail++; q->data[q->tail] = node; return; } int empty(Queue *q) { if (q->head > q->tail) { return 1; } else { return 0; } } Node *front(Queue *q) { return q->data[q->head]; } void pop(Queue *q) { if (empty(q)) { return; } else { q->head++; return; } } void clear_queue(Queue *q) { free(q->data); free(q); } void output(Queue *q) { if (empty(q)) { return; } else { Queue *output = (Queue *)malloc(sizeof(Queue)); init_queue(output, 100); for (Node *node = q->data[q->tail]; node != q->data[q->head]; node = q->data[node->pre]) { push(output, node); } push(output, q->data[q->head]); //不要遗漏! for (int i = output->tail; i >= output->head; --i) { i == output->tail || printf("=>"); printf("%d (%d, %d)", output->data[i]->pre, output->data[i]->x, output->data[i]->y); } printf("\n"); return; } } int check(int x, int y) { if (x >=0 && x < 10 && y >=0 && y < 10) { return 1; } else { return 0; } } void solve_maze(int x0, int y0, int x1, int y1) { Queue *q = (Queue *)malloc(sizeof(Queue)); Queue *path = (Queue *)malloc(sizeof(Queue)); init_queue(q, 100); init_queue(path, 100); Node *start_node = (Node *)malloc(sizeof(Node)); init_node(start_node, x0, y0, -1); push(q, start_node); maze[x0][x1] = -1; int id = -1; while (!empty(q)) { Node *cur_node = front(q); push(path, cur_node); pop(q); id++; if (cur_node->x == x1 && cur_node->y == y1) { output(path); printf("Success!\n"); return; } for (int i = 0; i < 4; i++) { if (check(cur_node->x + direct[0][i], cur_node->y + direct[1][i]) && maze[cur_node->x + direct[0][i]][cur_node->y + direct[1][i]] == 0) { Node *tmp = (Node *)malloc(sizeof(Node)); init_node(tmp, cur_node->x + direct[0][i], cur_node->y + direct[1][i], id); push(q, tmp); maze[cur_node->x + direct[0][i]][cur_node->y + direct[1][i]] = -1; } } } printf("Failed!\n"); return; } int main() { int x0, y0, x1, y1; scanf("%d%d%d%d", &x0, &y0, &x1, &y1); solve_maze(x0, y0, x1, y1); return 0; }
【易错点记录】
- 赋值“=”与等于“==”不要弄混了;
- 注意for循环中间的不是停止条件而是继续条件!!!
- 结构体的初始化操作不要忘记!
- 多检查和对停止与边界条件!尤其是开头和和结尾的结点不要在条件判断后遗漏了!!
例题二:(求走法)
例题一是最简单的带障碍物迷宫问题,下面增加限制条件:每个位置只能访问一次,求一种有多少种走法。
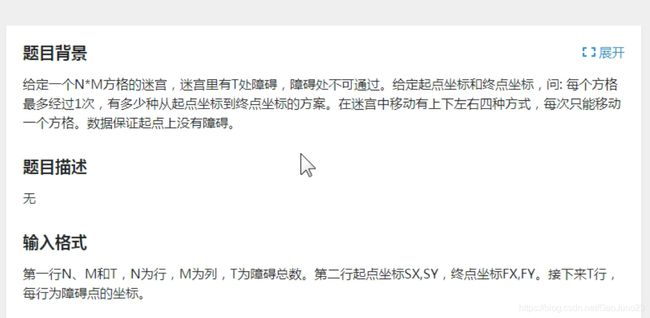
一般不求最短路径,只统计走法数,我们采用DFS递归的形式来解题。
代码实现(C)
#include <stdio.h> #include <stdlib.h> #include <string.h> int **maze; int direct[4][2] = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}}; int count = 0; int **visited; int check(int x, int y) { if (x >=0 && x < 10 && y >=0 && y < 10) { return 1; } else { return 0; } } void output(int n, int m) { for (int i = 0; i < n; i++) { for (int j = 0; j < m; j++) { j == 0 || printf(" "); printf("%d", maze[i][j]); } printf("\n"); } } void dfs(int x0, int y0, int x1, int y1) { if (x0 == x1 && y0 == y1) { count++; printf("\n"); return; } for (int i = 0; i < 4; i++) { int newx = x0 +direct[i][0]; int newy = y0 +direct[i][1]; if (check(newx, newy) && maze[newx][newy] == 0 && visited[newx][newy] == 0) { visited[newx][newy] = 1; printf("=>(%d, %d)", newx, newy); dfs(newx, newy, x1, y1); visited[newx][newy] = 0; } } } /*测试用例 5 5 8 0 0 4 4 1 1 1 2 1 3 2 1 2 3 3 1 3 3 3 2 */ int main() { int n, m, t; scanf("%d%d%d", &n, &m, &t); int x0, y0, x1, y1; scanf("%d%d%d%d", &x0, &y0, &x1, &y1); maze = (int **)malloc(sizeof(int *) * n); visited = (int **)malloc(sizeof(int *) * n); for (int i = 0; i < n; i++) { maze[i] = (int *)malloc(sizeof(int) * m); visited[i] = (int *)malloc(sizeof(int) * m); memset(maze[i], 0 ,sizeof(int) * m); memset(visited[i], 0 ,sizeof(int) * m); } int x, y; for (int i = 0; i < t; i++) { scanf("%d%d", &x, &y); maze[x][y] = 1; } output(n, m); if (!check(x0, y0) || !check(x1, y1)) { printf("ERROR!\n"); } else { printf("(%d, %d): \n", x0, y0); visited[x0][y0] = 1; dfs(x0, y0, x1, y1); printf("%d\n", count); } return 0; } /*输出 0 0 0 0 0 0 1 1 1 0 0 1 0 1 0 0 1 1 1 0 0 0 0 0 0 (0, 0): =>(1, 0)=>(2, 0)=>(3, 0)=>(4, 0)=>(4, 1)=>(4, 2)=>(4, 3)=>(4, 4) =>(0, 1)=>(0, 2)=>(0, 3)=>(0, 4)=>(1, 4)=>(2, 4)=>(3, 4)=>(4, 4) 2*/
【易错点记录】
memset函数的二维数组初始化:
- 声明二维数组a[n][n],则可以用memset(a,0x3f,sizeof(a))。因为声明的二维数组存储单元是连续的。
- 但是动态声明的二维数组指针int **q只能够每次获取q[i]后对每行进行初始化,因为指针对于每行的存储单元不连续。
棋盘马走日问题
无障碍
例题一:(遍历)
输入:国际象棋的棋盘是$8 x 8$的方格(按顺序编号1~64)。现在给定马的起始位置,遍历整个棋盘,要求每个方格有且仅访问一次。
输出:遍历路径(编号序列)。
解题思路
dfs递归遍历,用栈存储路径,起点任意(不一定有解)。
代码实现(C)
#include <stdio.h> #include <stdlib.h> #include <string.h> int direct[8][2] = {{1, 2}, {2, 1}, {-1, -2}, {-2, -1}, {1, -2}, {2, -1}, {-1, 2}, {-2, 1}}; int **maze; int **visited; typedef struct Stack { int *id; int top_index, length; } Stack; void init_stack(Stack *s, int size) { s->length = size; s->id = (int * )malloc(sizeof(int) * size); s->top_index = -1; return; } void push(Stack *s, int id) { if (s->top_index + 1 >= s->length) { return; } s->top_index++; s->id[s->top_index] = id; } int empty(Stack *s) { if (s->top_index < 0) { return 1; } else { return 0; } } int top(Stack *s) { return s->id[s->top_index]; } void pop(Stack *s) { if (empty(s)) { return; } else { s->top_index--; return; } } void clear(Stack *s) { free(s->id); free(s); return; } int check(int x, int y) { if (x < 0 || y < 0 || x >= 8 || y >= 8 ) { return 0; } else { return 1; } } void output(Stack *s) { for (int i = 0; i < s->top_index; i++) { i == 0 || printf("=>"); printf("%d", s->id[i]); } printf("\n"); return; } void output_maze() { for (int i = 0; i < 8; i++) { for (int j = 0; j < 8; j++) { j == 0 || printf(" "); printf("%d", maze[i][j]); } printf("\n"); } return; } Stack *path; int flag; void bianli_dfs(int x, int y) { visited[x][y] = 1; push(path, maze[x][y]); output(path); while (!empty(path)) { if (path->top_index == 63) { printf("Find!\n"); output(path); flag = 1; return; } int id = top(path); int cur_x = id / 8; int cur_y = id % 8; int newx, newy; for (int i = 0; i < 8; i++) { newx = cur_x + direct[i][0]; newy = cur_y + direct[i][1]; if (check(newx, newy) && visited[newx][newy] == 0) { bianli_dfs(newx, newy); if (flag ==1) { return; } } } pop(path); visited[cur_x][cur_y] = 0; } return; } void free_mat(int **mat) { for (int i = 0; i < 8; i++) { free(mat[i]); } free(mat); } int main() { maze = (int **)malloc(sizeof(int *) * 8); visited = (int **)malloc(sizeof(int *) * 8); int id = 1; for (int i = 0; i < 8; i++) { maze[i] = (int *)malloc(sizeof(int) * 8); visited[i] = (int *)malloc(sizeof(int) * 8); memset(visited[i], 0 ,sizeof(int) * 8); for (int j = 0; j < 8; j++) { maze[i][j] = id++; } } //output_maze(); int x, y; printf("Please enter the start coordinate: (x, y)\n"); fflush(stdout); scanf("(%d, %d)", &x, &y); if (!check(x, y)) { printf("ERROR\n"); } else { path = (Stack *)malloc(sizeof(Stack)); init_stack(path, 64); bianli_dfs(x, y); } free_mat(maze); free_mat(visited); return 0; }
例题二:(求最短路径)
题目描述
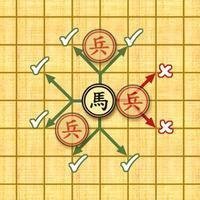
在国际象棋中,马的走法与中国象棋类似,即俗话说的“马走日”,下图所示即国际象棋中马每一步能到达的格子(箭头所指为每步到达位置)。现有一200 * 200大小的国际象棋棋盘,棋盘中仅有一个马,给定马的当前位置和目标位置,求出马最少需要多少跳才能从当前位置到达目标位置。
输入格式:已有文件txt格式文件里每一行有四个以空格分隔的整数,分别表示马当前位置及目标位置的横、纵坐标(Xs,Ys)和(Xe,Ye)。坐标由0开始。
文件输入样例:
1 1 2 1
1 5 5 1
输入说明第一行:马的当前位置为(1,1),目标位置为(2,1)。第二行:马的当前位置为(1,5),目标位置为(5,1)。
输出:文件里每一行第一个数字为1个整数,即马从当前位置跳到目标位置最少的跳数,然后以空格隔开,输出对应的最短路径坐标,坐标格式为(X, Y),每个坐标之间以空格隔开。所有路径输出后以回车换行。
输出样例:
3 (1, 1) (3, 2) (4, 0) (2, 1)
4 (1, 5) (2, 3) (4, 2) (6, 3) (5, 1)
第一行:马需要跳3次才可以从(1,1)到(2,1),对应的路径为(1, 1) (3, 2) (4, 0) (2, 1)。第二行:马需要跳4次才可以从(1,5)到(5,1),对应的路径为(1, 5) (2, 3) (4, 2) (6, 3) (5, 1)。
解题思路
队列bfs循环,注意最后输出路径的顺序,不要遗漏起点!
代码实现(C)
#include <stdio.h> #include <stdlib.h> #include <string.h> #define N 200 #define M 200 int direct[8][2] = {{1, 2}, {2, 1}, {-1, -2}, {-2, -1}, {1, -2}, {2, -1}, {-1, 2}, {-2, 1}}; int **maze; typedef struct Node { int x, y, pre; } Node; Node *create_node(int x, int y, int pre) { Node *node = (Node *)malloc(sizeof(Node)); node->x = x; node->y = y; node->pre = pre; return node; } typedef struct Queue { Node **data; int head, tail, length; } Stack; void init_queue(Queue *q, int size) { q->length = size; q->data = (Node **)malloc(sizeof(Node *) * size); q->tail = -1; q->head = 0; return; } void push(Queue *q, Node *node){ if (q->tail + 1 >= q->length) { return; } q->tail++; q->data[q->tail] = node; return; } int empty(Queue *q) { if (q->head > q->tail) { return 1; } else { return 0; } } Node *front(Queue *q) { if (!empty(q)) { return q->data[q->head]; } return NULL; } void pop(Queue *q) { if (!empty(q)) { q->head++; } } void clear_queue(Queue *q) { free(q->data); free(q); return; } int check(int x, int y) { if (x < 0 || y < 0 || x >= N || y >= M ) { return 0; } else { return 1; } } void output(Queue *q) { int count = 0; Queue *res = (Queue *)malloc(sizeof(Queue)); init_queue(res, N * M); for (Node *node = q->data[q->tail]; node != q->data[q->head]; node = q->data[node->pre]) { count++; push(res, node); } push(res, q->data[q->head]); printf("%d ", count); for (int i = res->tail; i >= res->head; i-- ) { printf("(%d, %d) ", res->data[i]->x, res->data[i]->y); } return; } void output_maze() { for (int i = 0; i < N; i++) { for (int j = 0; j < M; j++) { j == 0 || printf(" "); printf("%d", maze[i][j]); } printf("\n"); } return; }void bfs(int sx, int sy, int ex, int ey) { Queue *q = (Queue *)malloc(sizeof(Queue)); init_queue(q, N *M); Queue *path = (Queue *)malloc(sizeof(Queue)); init_queue(path, N *M); int pre = -1; Node *start_node = create_node(sx, sy, pre); push(q, start_node); maze[sx][sy] = 1; while (!empty(q)) { Node *cur_node = front(q); pop(q); push(path, cur_node); //output(path); ++pre; if (cur_node->x == ex && cur_node->y == ey) { output(path); free(path); free(q); return; } for (int i = 0; i < 8; i++) { int newx = cur_node->x + direct[i][0]; int newy = cur_node->y + direct[i][1]; if (check(newx, newy) && maze[newx][newy] == 0) { Node *new_node = create_node(newx, newy, pre); maze[newx][newy] = 1; push(q, new_node); } } } return; } void free_mat(int **mat) { for (int i = 0; i < 8; i++) { free(mat[i]); } free(mat); } int main() { maze = (int **)malloc(sizeof(int *) * N); for (int i = 0; i < N; i++) { maze[i] = (int *)malloc(sizeof(int) * M); memset(maze[i], 0 ,sizeof(int) * M); } //output_maze(); int sx, sy, ex, ey; scanf("%d%d%d%d", &sx, &sy, &ex, &ey); if (!check(sx, sy) || !check(ex, ey)) { printf("ERROR\n"); } else { bfs(sx, sy, ex, ey); } free_mat(maze); return 0; }
例题三:(求走法)
解题思路
一般统计走法推荐dfs递归,实现简单快捷。
代码实现(C)
#include <stdio.h> #include <stdlib.h> #include <string.h> int direct[8][2] = {{1, 2}, {2, 1}, {-1, -2}, {-2, -1}, {1, -2}, {2, -1}, {-1, 2}, {-2, 1}}; int **maze; int n, m; int count = 0; int len = 1; typedef struct Node { int x, y, pre; } Node; Node *create_node(int x, int y, int pre) { Node *node = (Node *)malloc(sizeof(Node)); node->x = x; node->y = y; node->pre = pre; return node; } int check(int x, int y) { if (x < 0 || y < 0 || x >= n || y >= n ) { return 0; } else { return 1; } } void output_maze() { for (int i = 0; i < n; i++) { for (int j = 0; j < m; j++) { j == 0 || printf(" "); printf("%d", maze[i][j]); } printf("\n"); } return; } void dfs_count(int x, int y) { if (len == n * m) { count++; } for (int i = 0; i < 8; i++) { int newx = x + direct[i][0]; int newy = y + direct[i][1]; if (check(newx, newy) && maze[newx][newy] == 0) { maze[newx][newy] = 1; len++; dfs_count(newx, newy); len--; maze[newx][newy] = 0; } } return; } void free_mat(int **mat) { for (int i = 0; i < 8; i++) { free(mat[i]); } free(mat); } int main() { int t, sx, sy; scanf("%d", &t); for (int i = 0; i < t; i++) { scanf("%d%d%d%d", &n, &m, &sx, &sy); if (n == 1 && m == 1) { printf("1\n"); break; } if (!check(sx, sy)) { printf("ERROR\n"); } else { maze = (int **)malloc(sizeof(int *) * n); for (int i = 0; i < n; i++) { maze[i] = (int *)malloc(sizeof(int) * m); memset(maze[i], 0 ,sizeof(int) * m); } maze[sx][sy] = 1; dfs_count(sx, sy); printf("%d\n", count); free_mat(maze); count = 0; } } return 0; }
带障碍物
骑马走江湖
别马脚:
参考资料:
https://www.cnblogs.com/huchong/p/8522453.html
https://www.it610.com/article/1295331529966297088.htm
https://blog.csdn.net/weixin_43564373/article/details/84101191
https://blog.csdn.net/fun_always/article/details/90115780
https://blog.csdn.net/fun_always/article/details/90115780


 浙公网安备 33010602011771号
浙公网安备 33010602011771号