螺旋矩阵与螺旋队列
螺旋矩阵
方形矩阵
问题描述
给定一个$N \times N$的方阵,其中元素为自然数,排列规则为按照顺时针螺旋方向单调递增(起始值为$1$,终点值为$N$)。举例如下:
若n = 3,螺旋矩阵为:
1 2 3 8 9 4 7 6 5
若n = 4,螺旋矩阵为:
1 2 3 4 12 13 14 5 11 16 15 6 10 9 8 7
若n = 5,螺旋矩阵为:
1 2 3 4 5 16 17 18 19 6 15 24 25 20 7 14 23 22 21 8 13 12 11 10 9
输入:$N$
输出:螺旋矩阵$N \timemsN$
解题思路
最简单直接的想法就是按照规则先申请好$N \timesN$的矩阵内存,然后按螺旋方向依次填入相应的元素,填充完毕后再双层循环打印出来。时间按复杂为O(n2),空间复杂度也为O(n2)。 Leetcode 59
//N阶螺旋方阵 #include <stdio.h> #include <stdlib.h> void output(int **mat, int n) { for (int i = 0; i < n; ++i) { for (int j = 0; j < n; ++j) { j == 0 || printf(" "); printf("%d", mat[i][j]); } printf("\n"); } } int main() { int n; scanf("%d", &n); int **mat = (int **)malloc(sizeof(int *) * n); for (int i = 0; i < n; i++) { mat[i] = (int *)malloc(sizeof(int) * n); } //初始化圆环边界 int rl = 0; int rh = n - 1; int cl = 0; int ch = n - 1; int now = 1; //圆环共有N/2 + 1个 while (1) { for (int j = cl; j <=ch; ++j) mat[rl][j] = now++; if (++rl > rh) break; for (int i = rl; i <= rh; ++i) mat[i][ch] = now++; if (--ch < cl) break; for (int j = ch; j >= cl; --j) mat[rh][j] = now++; if (--rh < rl) break; for (int i = rh; i >= rl; --i) mat[i][cl] = now++; if (++cl >ch) break; } output(mat, n);
return 0; }
按照矩阵规律填充元素时,我们是随机访问矩阵元素的(如果可以按顺序访问,根本不用先存起来再打印)。随机访问内存,效率当然不高。所以即使时间复杂度已为最优,但那只是理论上的最优,在实践中表现并不一定就好。
假如能根据行列号直接计算出对应的矩阵元素就好了。当$N$给定后,这个矩阵就已经唯一确定了,那么每一个元素也是确定的。也就是说,每一个位置放什么元素仅仅取决于$N$。因此我们可以找到一个函数$element(i, j)$,将行号$i$和列号$j$映射成对应这个行列号的元素。当然这个函数肯定不是一个简单的函数,不是一眼就可以看出来的,但也并不是不可能。
现在我们就来考查一下这个矩阵有什么特点。注意观察一下螺旋矩阵的最外层,它的左上角的元素是最小的,然后沿顺时针方向递增,就如同一个环一样(比如$N$为4时,$1, 2, ..., 12$就是最外面一层环)。再往里面一层,也是一样,顺时针方向递增的一个环(比如$N$为$4$时,$13, 14, 15, 16$就是里面一层环)。以此类推,环里面还有一层环($N$为$4$时有$2$层环,$N$为$5$时有$3$层环,最里面一层只有一个元素$25$),实际上是一个圆环套圆环结构。每一圆环最关键的元素就是左上角的那一个元素。只要知道了这个元素,再加上这个正方形环的边长就可以计算出剩下的元素。设左上角元素为$pos$,边长为$len$,以左上角为原(行号和列号均为0),其它元素的行号和列号都以它作参考,则$element(i, j)$的计算方法如下所示:
1. 若$i == 0$,$element(i, j) = pos + j$;
2. 否则若$j == 0$,$element(i, j) = pos + 4 * (len - 4) - (i - 1) - 1$;
3. 否则若$i == len - 1$,$element(i, j) = pos + 4 * (len - 4) - (len - 2) - 1 - j$;
4. 否则$element(i, j) = pos + len - 1 + i$;
详细的函数计算步骤见如下代码:
//顺序访问存储顺时针螺旋矩阵 //访问矩阵元素O(1) #include <stdio.h> #include <stdlib.h> #define min(a, b) ((a < b) ? (a) : (b)) #define max(a, b) ((a >= b) ? (a) : (b)) #define abs(a) ((a >= 0) ? (a) : (-a)) int calc(int n, int pos) { if (pos == 0) { return 1; } else { return 4 * (n - pos * 2 + 1) + calc(n, pos - 1); } } int element(int n, int i, int j) { int pos = min(min(i, n - 1 -i) , min(j, n - 1 - j)); int len = n - pos * 2; int base = calc(n, pos); //printf("pos = %d, base = %d, len = %d\n", pos, base, len); if ( i == pos) { return base + j - pos; } else if (j == pos) { return base + (len - 1) * 4 - i + pos; } else if (i == pos + len - 1) { return base + 3 * (len - 1) - j + pos; } else { return base + (len - 1) + i - pos; } } int main() { int n; scanf("%d", &n); for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { j == 0 || printf(" "); printf("%d", element(n, i, j)); //element(n, i, j); } printf("\n"); } }
一般矩阵NxM
打印一般矩阵与方阵的思路基本一致,以上代码稍微改动即可。下面讲讲其它常见的题型。
问题描述
输入:$N$行$M$列矩阵;
输出:顺时针螺旋序列;
解题思路
双百答案直接采用画圈思维,确定上下左右四个边界,画一条边就更新对应的边界,并做判断(是否画完)。
代码实现(C)
int* spiralOrder(int** matrix, int matrixSize, int* matrixColSize, int* returnSize){ if (matrixSize == 0) { *returnSize = 0; return NULL; } * returnSize = matrixSize * (*matrixColSize); int *arr = (int *)malloc(sizeof(int) * (*returnSize)); int cl = 0; int ch = (*matrixColSize) - 1; int rl = 0; int rh = matrixSize - 1; int now = 0; while (1) { for (int j = cl; j <= ch; ++j) arr[now++] = matrix[rl][j]; if (++rl > rh) break; for (int i = rl; i <= rh; ++i) arr[now++] = matrix[i][ch]; if (--ch < cl) break; for (int j = ch; j >= cl; --j) arr[now++] = matrix[rh][j]; if (--rh < rl) break; for (int i = rh; i >= rl; --i) arr[now++] = matrix[i][cl]; if (++cl > ch) break; } return arr; }
【注意】这题有个坑!刚开始要检查输入数组是否为空(matrixSize == 0),不然一提交就会报错数组越界。
Leetcode 885
问题描述
在 R 行 C 列的矩阵上,我们从 (r0, c0) 面朝东面开始
这里,网格的西北角位于第一行第一列,网格的东南角位于最后一行最后一列。
现在,我们以顺时针按螺旋状行走,访问此网格中的每个位置。
每当我们移动到网格的边界之外时,我们会继续在网格之外行走(但稍后可能会返回到网格边界)。
最终,我们到过网格的所有 R * C 个空间。
按照访问顺序返回表示网格位置的坐标列表。

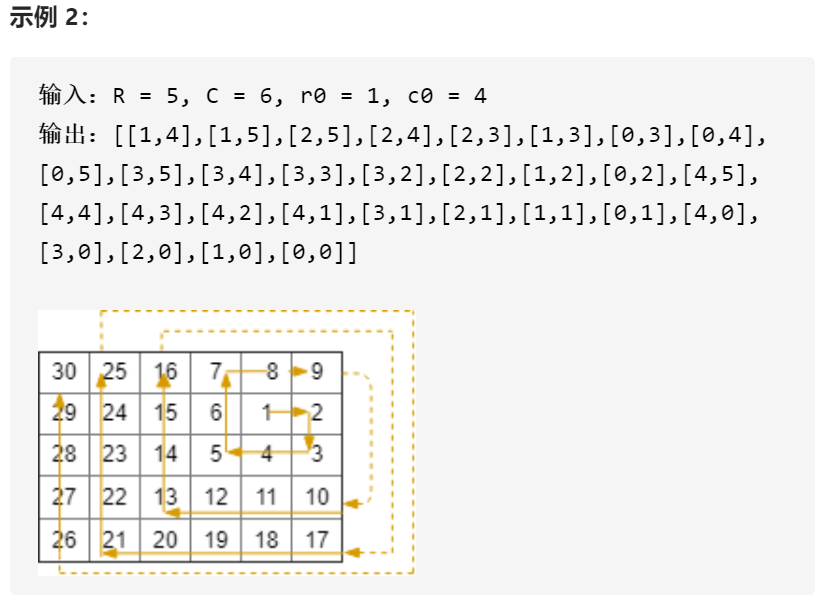
C语言渣题解
//Leetcode 885 int** spiralMatrixIII(int R, int C, int r0, int c0, int* returnSize, int** returnColumnSizes){ * returnSize = R * C; * returnColumnSizes = (int *)malloc(sizeof(int) * (*returnSize)); int **mat = (int **)malloc(sizeof(int *) * (*returnSize)); for (int i = 0; i < * returnSize; i++) { mat[i] = (int *)malloc(sizeof(int) * 2); (* returnColumnSizes)[i] = 2; } int cl = c0; int ch = c0; int rl = r0; int rh = r0; int now = 0; #define max(a, b) ((a) >= (b) ? (a) : (b)) #define min(a, b) ((a) <= (b) ? (a) : (b)) while (cl >= 0 || rl >= 0 || ch < C || rh < R) { if (ch < C) { for (int i = max(rl + 1, 0); i < min(R, rh); i++) { mat[now][0] = i; mat[now][1] = ch; now++; } } if (rh < R) { for (int j = min(C - 1, ch); j >= max(0, cl); --j) { mat[now][0] = rh; mat[now][1] = j; now++; } } if (cl >= 0 && cl < ch) { for (int i = min(R - 1, rh - 1); i >= max(0, rl + 1); --i) { mat[now][0] = i; mat[now][1] = cl; now++; } } if (rl >= 0 && rl < rh) { for (int j = max(0, cl); j <= min(C - 1, ch); ++j) { mat[now][0] = rl; mat[now][1] = j; now++; } } rl--; rh++; cl--; ch++; } return mat; }
螺旋队列
螺旋队列长这样:
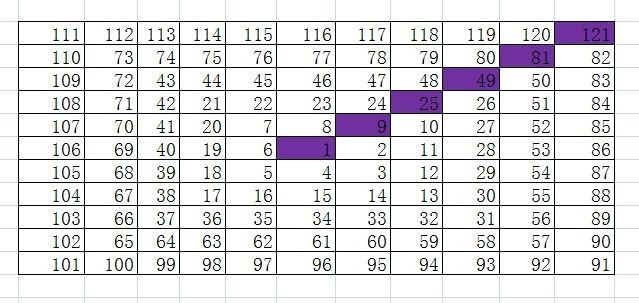
不难发现他的排列规律主要有两点:
- 顺时针螺旋,自然数递增
- 右斜上对角线数字(紫色)为奇数平方向上递增,且值与所在圈数有关
问题描述
设1的坐标是(0,0),x方向向右为正,y方向向下为正,如图所示:
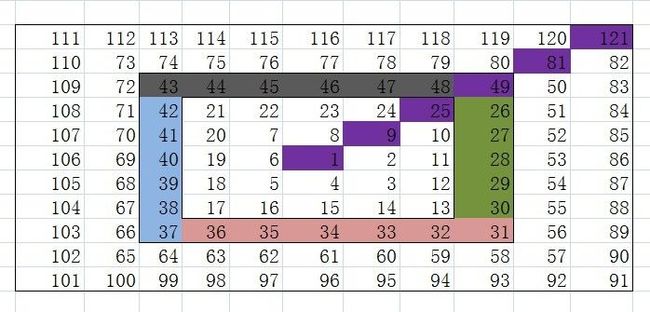
例如,7的坐标为(-1,-1),2的坐标为(1,0)。编程实现输入任意一点坐标(x,y),输出所对应的数字。
解题思路
与螺旋矩阵类似的核心思路:画圈=>找到每一圈的基准点=>四条边上的元素相对于起始点的位置关系推出值的关系。
具体说来,设圈数从$0$开始编号。则有
- 不难看出紫色元素为所在圈最大值$max$,将它最为本圈的基准点(坐标为$(r, r)$)。紫色元素取值为$1^2, 3^2, 5^2, 7^2, \dots$,与圈数编号$r$的关系:$max = (2 * r + 1)^2$。本圈(方形)边长为$len = 2 * r + 1$,则易得本圈最小值即它的正下方元素$min = max - 4 * (2 * r + 1 - 1) + 1 = (2 * r - 1)^2 + 1$。
- 得到基准点元素值后,四条边的元素值对应坐标的关系就很容易得到了:
上边:$top = max - r + x$;
左边:$left= max - 3 * r - y$;
下边:$bottom = max - 5 * r - x$;
右边:$right = max - 7 * r + y$;
代码实现
#include <stdio.h> #include <stdlib.h> #define max(a, b) ((a) >= (b) ? (a) : (b)) #define abs(a) ((a) >= (0) ? (a) : (-a)) int findvalue(int x, int y) { int r = max(abs(x), abs(y)); int max = (2 * r + 1) * (2 * r + 1); //printf("x = %d, y = %d\nr = %d, max = %d\n", x, y, r, max); if ( y == -r) { return max - r + x; } else if ( x == -r) { return max - 3 * r - y; } else if ( y == r) { return max - 5 * r - x; } else if ( x == r) { return max - 7 * r + y; } } int main() { int x , y; printf("请输入目标元素的坐标(x, y),以空格分隔:\n"); fflush(stdout); scanf("%d%d", &x, &y); fflush(stdout); printf("\n目标元素值为:%d, 下面输出相应的螺旋队列检验:\n", findvalue(x, y)); for (int j = -y; j <= y; j++) { for (int i = -x; i <= x; i++) { i == -x || printf(" "); printf("%-5d", findvalue(i, j)); } printf("\n"); } fflush(stdout); return 0; }
【注意】
- 输出的矩阵坐标和题目给定的平面直角坐标系不同,两者相当于行列互换了!
- %-5d控制输出对齐,fflush(stdout)清空缓冲区,保证第一个输出在输入之前显示。
参考资料:
https://blog.csdn.net/songzitea/article/details/8348243
https://blog.csdn.net/Chen_Swan/article/details/105799956
https://www.it610.com/article/1543831.htm
它的正下方一位为本圈最小值$min$。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号