斐波那契数列的性质

斐波那契递推式：

---

---

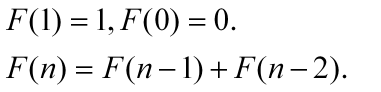
斐波那契通项公式：

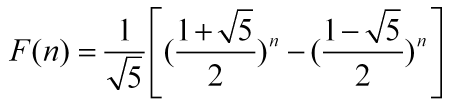
求证过程如下：

---

---

 

斐波那契和矩阵的关系：

描述这个。那还是描述矩阵和线性递推式的关系吧

线性递推式。即F(n)和F(n-1),F(n-2),F(n-3),F(n-4)...其阶均是一次的关系。

如F(n)=2F(n-1)+F(n-2).F(n)=F(n-1)+2F(n-3)+4F(n-4)...

矩阵可以求解这样的递推式。也就是说可以快速计算F(n).时间复杂度可以到达log(n)级别。

 

先介绍一下我们需要用到的关于矩阵的知识。

描述矩阵规模时：n行m列。即大小为n*m.

矩阵乘法：

 

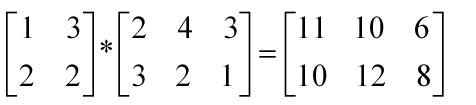
形状上：2*2 和 2*3 的矩阵乘积后,结果是2*3的矩阵。

           即 a*b 矩阵 和 c*d的矩阵乘积结果是a*d的矩阵。             其中b和c必须相等。原因看下面。

运算法则：对于结果矩阵的第i行第j列的位置的结果是由前一个矩阵的对应的行。和后一个矩阵对应的列。对应位置  　　　　　乘积和获得的。比如第1行第1列的11.是由前矩阵的第一行(1,3)和后矩阵的第一列(2,3)对应位置乘　　　　　　积和。1*2+3*3 = 11 获得的。如果上述b和c如果不相等。那么会有地方"失配"没有数值可以进行　　　　　　计算。不符合矩阵乘法定义。

矩阵乘法性质：

　　　　　矩阵乘法不符合交换律。符合结合律。（具体不分析了。稍加思考即得。）

 

矩阵的幂运算：

即计算以下式子。

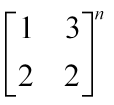
其中朴素想法可以通过一步一步矩阵乘法来获得结果矩阵。

但是从宏观角度上去想。我们把矩阵的乘法理解成一种普通的数的乘法。我们现在要计算数的幂。

可以类比快速幂。那么矩阵也有矩阵的快速幂。分治思想。具体实现其实就是快速幂把乘法那部分改成矩阵乘法即可。代码百度上有很多。等下我会放一份。（acdreamer矩阵的模板）

 

矩阵计算递推式。

比如:对于F(n)=aF(n-1)+bF(n-2)

我们可以构造矩阵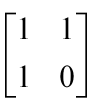和矩阵

二者乘积为：

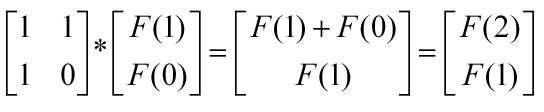
会发现经过一次乘积。我们可以获得矩阵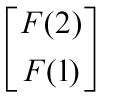。那么我们再将这个矩阵乘一次

就会得到F(3),F(2)的矩阵。所以我们可以发现。只要我们将我们的初始矩阵乘我们构造出来的1,1,1,0矩阵n-1次。就能获得F(n),F(n-1)的矩阵。然后F(n)就是我们想要的了。而乘n-1次1,1,1,0矩阵。根据结合律。我们可以让1,1,1,0矩阵自乘n-1次。最后再乘初始矩阵即可获得最后我们想要的结果。

即求。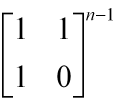我们可以利用快速矩阵幂。就可以在log(n)复杂度中解决了。

 

---

---

关于斐波那契的一些恒等式：

 

 

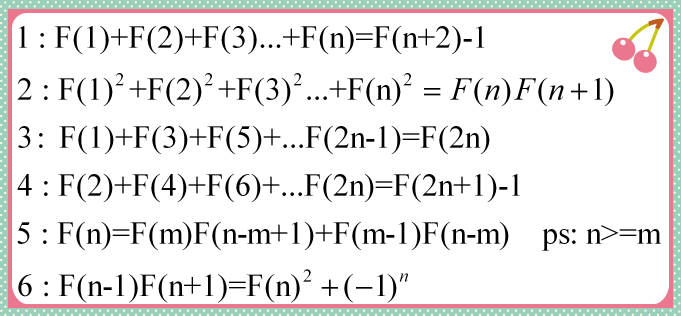
具体证明：1~4.都是用类似的方法。我提一提。就好吧。

比如1. F(1)=F(3)-F(1) ， F(2)= F(4)-F(3)。。。F(n)=F(n+2)-F(n+1)

类似的分解。然后求和就能获得结果了。

对于5.F(n)=F(n-1)+F(n-2)

　　　F(n)=2F(n-2)+F(n-3)

　　　F(n)=3F(n-3)+2F(n-4)

　　　...

　　　F(n)=F(m)F(n-m+1)+F(m-1)F(n-m)

对于6.是个很著名的式子。要想知道证明。百度有好多。就不赘述了。（而且现在还没用过这个式子。）

---

---

斐波那契的数论相关：

性质1：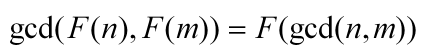

证明：先证明斐波那契数列相邻两项是互素的。

反证法:假设不互素。那么有a=gcd(F(n),F(n-1)),a>1.

　　　 那么对于F(n)=F(n-1)+F(n-2).因为a|F(n),a|F(n-1),所以a|F(n-2).

　　　由于a|F(n-1),a|F(n-2).又可以获得a|F(n-3)...可以知道a|F(1)其中。F(1)=1.

　　　如果a|F(1)->a|1那么与a>1不符。相邻互素得证.(其实 a|F(2)就已经不行了.)　　　　

　　　

　　　那么再由上面斐波那契恒等式5.可以推理。

　　　

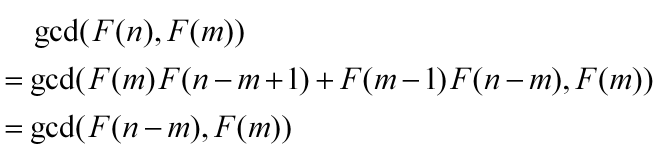
　　　中间推导依靠一小点数论知识.观察开始式子和结果。

　　　一直将上式递推下去。结合gcd(n,m)=gcd(n-m,m).结果会是gcd(a,b) = gcd(0,gcd(a,b))

　　　那么就可以证明上述式子成立。

 

性质2：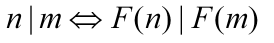

证明:当n|m时。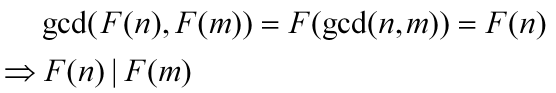

 

　　必要性也可以通过类似手法得证。

 

 

#include<iostream>
#include<stdio.h>
#include<string.h>
#include<string>
#include<algorithm>
#define LL long long
#define N 2
#define MOD 100000007
using namespace std;

struct Matrix
{
    LL m[N][N];
};

Matrix A = {
    1,1,
    1,0
};
Matrix I = {
    1,0,
    0,1
};
Matrix multi(Matrix a,Matrix b)
{
    Matrix c;
    int i,j,k;
    for(i=0;i<N;i++)
    {
        for(j=0;j<N;j++)
        {
            c.m[i][j] = 0;
            for(k=0;k<N;k++)
            {
                c.m[i][j] += a.m[i][k] * b.m[k][j] % MOD;
            }
            c.m[i][j] %= MOD;
        }
    }
    return c;
}
Matrix mat_pow(Matrix A,int k)
{
    Matrix ans = I,p = A; //为了 不更改I 和 A
    while(k)
    {
        if(k&1)
        {
            ans = multi(ans,p);
        }
        k >>= 1;
        p = multi(p,p);
    }
    return ans;
}

int main()
{
    int n;
    while(scanf("%d",&n)!=EOF)
    {
        Matrix ans = mat_pow(A,n-1);
        printf("%I64d\n",ans.m[0][0]);
        
    }
    return 0;
}