片集 - 树上问题 - 1
欢迎来看 “片” (的简介)
由于-\(看片\)-生涯转瞬即逝,于是我选择对“\(片\)”进行一定的总结:
相信你一定看懂了
由于开始的时间有一点晚,就姑且认为我以后会慢慢补充吧......
回到总部
点分治 \(P4178\) \(Tree\)
解: 树的重心,树上\(DFS\)搜索,点分治
经过(两)天 (一) 夜的鏖战,总算 \(\mathcal{TM}\) 的是把这个历史遗留问题解决了:
\(——点分治——\)
其实还有边分治
有挺多道题的,主要分享两道模板,废话,但只细讲一道
先从上面那道题开始。
暴力的想法就是往下找嘛吗,小小的加一个树上差分,估摸一下应该有个 \(\mathcal{O}(n^2)\),卡卡不就过了,继续思考,看看题解,有一个初步的想法,一棵树,能长成个什么样子嘛,初步设想一个小 \(\text{DP}\):
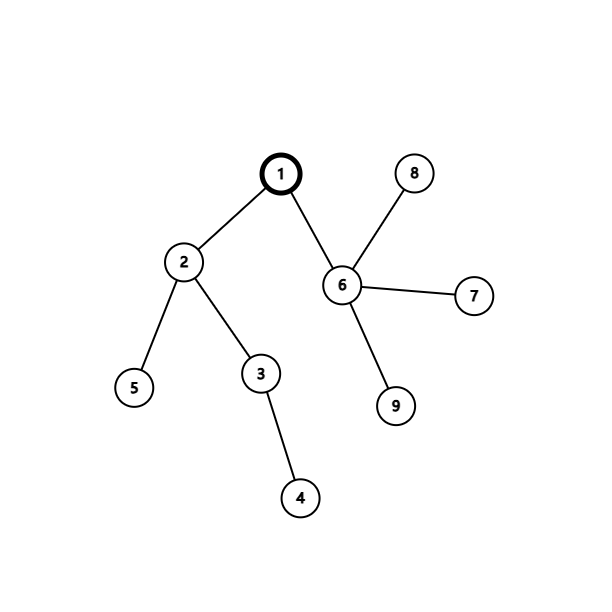
假设我们以 \(1\) 为根,那么它一名伸出来的两点距离要么在其子树中,要么或这直接由 \(1\) 引申出来,要么跨过 \(1\),显然第二种讨论可以自己消化掉,即跨过 \(1\) 的情况由两个由 \(1\) 引申出来的情况来消化,若从这里开始思考,还会有一些问题,比如设有 \(u\), \(v\)两个点的 \(\text{LCA}\) 不等于 \(1\) 那显然这个时候有多余的情况,怎么办?很简单,在往下递归的过程中记录这个子树的答案,然后在 \(1\) 的答案里扣就可以了。
那么接下来考虑处理答案,首先将所有的权值进行排序,然后双指针秒了。
想一想排序 \(\mathcal{O}(nlogn)\),再加一个根估计得有个 \(\mathcal{O}(n^2logn)\),这基本就没什么用,排序等方面先不管,考虑这个根能不能进行一系列的优化,模式化的,就出现了重心,一个最大的子树大小一定不超过过 \(\frac{sz}{2}\) 的抽象,这个时候,题解就会告诉你:
时间复杂的优化到了 \(\mathcal{O}(nlog^2n)\)
接下来的东西只针对于还是个 \(\mathcal{SB}\) 的我:
why????
你肯定觉得每一个东西都会作为根,拼什么就优化了呢,实际上,这时从最开始就没有理解的表现,所谓的 \(nlogn\), 实际是对于每一个子树的排序,就比如建一个有根树,我们排序所针对的并不是正一棵树,而是他的子节点。
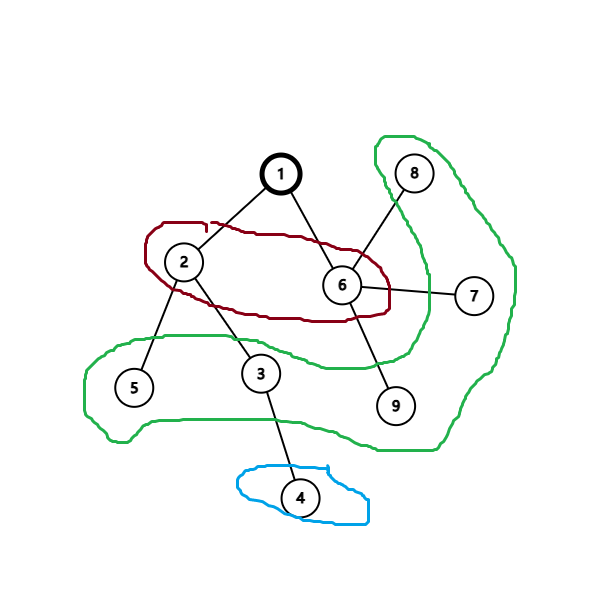
例如红就会排\(\textcolor{green}{绿}\)和\(\textcolor{blue}{蓝}\),\(\textcolor{green}{绿}\)就会排\(\textcolor{blue}{蓝}\),所以实际上所谓的 \(\mathcal{O}(n^2logn)\) 是一个及其保守党的估计,事实上最接近他的情况也只不过是当出现一整条链往下排的情况,然而再怎么保守,也会被可爱可敬的出题人发现,因此就有了这个神仙的优化:
重心
直接点说就是 \(n^2logn\) 的其中一个 \(n\) 代表的就是深度之类的东西。
由于加了重心之后最大的子树都只会有不到一半的大小那么这样递归下去,每一次大小都少一半,那么等到这棵树被我榨干了的时候就只需要 \(logn\) 次,所以这个时间复杂度是 \(\mathcal{O}(nlog^2n)\)
嘿嘿嘿,就好了,注意每一层都要找重心哦。
然后就是实践,由于妈妈在催着睡觉,我就先直接放代码了
点击查看代码
#include <iostream>
#include <cstring>
#include <algorithm>
#define ll long long
#define endl '\n'
using namespace std;
const int MAXN=4e4+5;
ll n,Q;
struct edge{
ll to,nxt,val;
};
edge e[MAXN<<1];
ll head[MAXN],tot=0;
void add_edge(ll u,ll v,ll w){
++tot;
e[tot].to=v;
e[tot].nxt=head[u];
head[u]=tot;
e[tot].val=w;
}
bool vis[MAXN];
ll sz[MAXN],wt[MAXN],rt=0,Tsz;
void GetRt(ll u,ll fath){//求重心,而且是每一棵子树
sz[u]=1;
wt[u]=0;
for (int i=head[u];i;i=e[i].nxt){
ll v=e[i].to;
if (v==fath || vis[v])
continue;
GetRt(v,u);
sz[u]+=sz[v];
wt[u]=max(wt[u],sz[v]);
}
wt[u]=max(wt[u],Tsz-sz[u]);
if (wt[u]<wt[rt]) rt=u;
}
ll dis[MAXN];
void Getval(ll u,ll fath,ll vl){//寻找权值
dis[++dis[0]]=vl;
for (int i=head[u];i;i=e[i].nxt){
ll v=e[i].to;
if (v==fath || vis[v]) continue;
Getval(v,u,vl+e[i].val);
}
}
ll m;
ll GetAns(ll u,ll vl){
dis[0]=0;
Getval(u,0,vl);
sort(dis+1,dis+dis[0]+1);
ll curans=0;
for (int l=1,r=dis[0];r>=1 && l<=r;r--){
while (dis[l]+dis[r]<=m && l<=r) curans+=r-l,++l;
}
return curans;
}
ll ans=0;
void dfs(ll u){
vis[u]=1;
ans+=GetAns(u,0);
for (int i=head[u];i;i=e[i].nxt){
ll v=e[i].to;
if (vis[v]) continue;
ans-=GetAns(v,e[i].val);
Tsz=sz[v];
wt[rt=0]=1145141919810ll;
GetRt(v,0);
dfs(rt);
}
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
memset(vis,0,sizeof(vis));
cin>>n;
for (int i=1;i<n;i++){
ll u,v,w;
cin>>u>>v>>w;
add_edge(u,v,w);
add_edge(v,u,w);
}
Tsz=n;
wt[rt=0]=1145141919810ll;
GetRt(1,0);
cin>>m;
dfs(rt);
cout<<ans<<endl;
}
详细解说就算了,毕竟都是自己的代码,肯定是看得懂的,小小阐述一下,大致就是几个部分,找重心,在树上正常递归,以及算答案。
重心不用多赘述了。
树上的递归与算答案紧密相连,先是算一下 \(u\) 自己本身的答案,这个时候的答案就是前面说的那个含有子节点路径重叠的点的贡献的答案,由 \(u\) 算到每一个 \(v\) 的时候,算一下 \(v\) 的答案,并在最终答案中减去,这个部分就是去掉非法贡献,注意这个过程中只是一次普通的递归,不要想多了,然后在当前的子树中找到对应的重心,再以重心继续跑。
这样,你就学会了 点分治 了
\(P3806\) \(【模板】\) \(点分治\) \(1\)
解:
唯一的区别就是这一次改成确切地询问了,那么双指针就没有必要了,直接记录求值即可,具体就自己看代码吧。
树链剖分 \(P3384\) \(【模板】\) \(重链剖分/树链剖分\)
解: 树链剖分,线段树
所谓的树链剖分:
顾名思义
就是
对树上的链进行剖析分类
咳咳
实际上就是这样,我们通过将树上的点通过特殊的编码方式,从而使得我们能够正常的使用数据结构解决问题,具体的,数据结构的优化是固定的,我们需要找到一种方式使得对于编码有一定规律可言的方式进行来用数据结构描述,前人想到了一个办法:
取重链*
*由中儿子连接而成的一条链,中儿子就是引导的子树大小最大的儿子
那么你就完成了,我们在记录 \(ChainId_u\) 描述 \(u\) 这个点的链的最开头。显然重链是连续的,故 \(dfn\) 序也是连续的,这样,我们就可以采用数据结构去优化了
时间复杂度就是数据结构的常驻 \(\mathcal{O}(nlogn)\)
放个代码:
点击查看代码
#include <iostream>
#define ll long long
#define endl '\n'
using namespace std;
const int MAXN=1e5+5;
ll n,m,rt,MOD;
struct edge{
ll to,nxt;
};
edge e[MAXN<<1];
ll tot=0,head[MAXN];
void add_edge(ll u,ll v){
++tot;
e[tot].to=v;
e[tot].nxt=head[u];
head[u]=tot;
}
ll nvl[MAXN];
ll WtSn[MAXN],sz[MAXN],dfn[MAXN],did[MAXN],ID=0,cid[MAXN]/*这个是CHAIN ID, 即所属的链中的头部*/;
ll fa[MAXN],dep[MAXN];
void dfsInit(ll u,ll fath){
sz[u]=1;
WtSn[u]=0;
for (int i=head[u];i;i=e[i].nxt){
ll v=e[i].to;
if (v==fath){
continue;
}
fa[v]=u;
dep[v]=dep[u]+1;
dfsInit(v,u);
sz[u]+=sz[v];
if (sz[v]>sz[WtSn[u]]){
WtSn[u]=v;
}
}
}
void dfs(ll u,ll fath){
cid[u]=fath;
dfn[++ID]=u;
did[u]=ID;
if (!WtSn[u]) return;
dfs(WtSn[u],fath);
for (int i=head[u];i;i=e[i].nxt){
ll v=e[i].to;
if (v==WtSn[u] || did[v]){
continue;
}
dfs(v,v);
}
}
struct Node{
ll val,tag;
};
Node a[MAXN<<3];
#define lson (id<<1)
#define rson (id<<1|1)
#define mid ((l+r)>>1)
void pushdown(ll id,ll l,ll r){
a[lson].tag=(a[id].tag+a[lson].tag)%MOD;
a[rson].tag=(a[id].tag+a[rson].tag)%MOD;
a[lson].val=(a[lson].val+(mid-l+1)*a[id].tag%MOD)%MOD;
a[rson].val=(a[rson].val+(r-mid)*a[id].tag%MOD)%MOD;
a[id].tag=0;
}
void pushup(ll id){
a[id].val=(a[lson].val+a[rson].val)%MOD;
}
void build(ll l,ll r,ll id){
a[id].tag=0;
if (l==r){
a[id].val=nvl[dfn[l]];
return;
}
build(l,mid,lson);
build(mid+1,r,rson);
pushup(id);
}
void modify(ll L,ll R,ll l,ll r,ll id,ll k){
if (L<=l && r<=R){
a[id].tag=(a[id].tag+k)%MOD;
a[id].val=(a[id].val+k*(r-l+1)%MOD);
return;
}
pushdown(id,l,r);
if (L<=mid) modify(L,R,l,mid,lson,k);
if (mid+1<=R) modify(L,R,mid+1,r,rson,k);
pushup(id);
}
ll query(ll L,ll R,ll l,ll r,ll id){
if (L<=l && r<=R){
return a[id].val%MOD;
}
ll sum=0;
pushdown(id,l,r);
if (L<=mid) sum=(query(L,R,l,mid,lson)+sum)%MOD;
if (mid+1<=R) sum=(query(L,R,mid+1,r,rson)+sum)%MOD;
return sum;
}
#undef lson
#undef rson
#undef mid
void M_chain(){
ll u,v,k;
cin>>u>>v>>k;
while (cid[u]!=cid[v]){
if (dep[cid[u]]<dep[cid[v]])
swap(u,v);
modify(did[cid[u]],did[u],1,n,1,k);
u=fa[cid[u]];
}
if (dep[u]<dep[v]){
swap(u,v);
}
modify(did[v],did[u],1,n,1,k);
}
void M_subtree(){
ll u,k;
cin>>u>>k;
modify(did[u],did[u]+sz[u]-1,1,n,1,k);
}
void Q_chain(){
ll u,v;
cin>>u>>v;
ll ans=0;
while (cid[u]!=cid[v]){
if (dep[cid[u]]<dep[cid[v]])
swap(u,v);
ans=(query(did[cid[u]],did[u],1,n,1)+ans)%MOD;
u=fa[cid[u]];
}
if (dep[u]<dep[v]){
swap(u,v);
}
ans=(query(did[v],did[u],1,n,1)+ans)%MOD;
cout<<ans<<endl;
}
void Q_subtree(){
ll u;
cin>>u;
cout<<query(did[u],did[u]+sz[u]-1,1,n,1)%MOD<<endl;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>m>>rt>>MOD;
for (int i=1;i<=n;i++){
cin>>nvl[i];
}
for (int i=1;i<n;i++){
ll u,v;
cin>>u>>v;
add_edge(u,v);
add_edge(v,u);
}
dfsInit(rt,0);
dfs(rt,rt);
build(1,n,1);
for (int i=1;i<=m;i++){
ll opt;
cin>>opt;
if (opt==1) M_chain();
if (opt==2) Q_chain();
if (opt==3) M_subtree();
if (opt==4) Q_subtree();
}
}
再附一道题,也是我学了树链剖分的直接原因*
解:树链剖分基本应用,玄学,随机化与勇气
树链剖分部分就不讲了,唯一要提一嘴的就是处理一个排列和的判断,\(\text{HYX}\) 说求平方和的失误概率极低,希望在正式比赛中,出题人不那么毒瘤,还有一些随机赋值求疑惑和然后树上差分,就不细讲了。
点击查看代码
#include <iostream>
#define ll long long
#define endl '\n'
using namespace std;
const int MAXN=5e5+5;
const ll MOD=998244353ll;
ll n,m,rt;
struct edge{
ll to,nxt;
};
edge e[MAXN<<1];
ll tot=0,head[MAXN];
void add_edge(ll u,ll v){
++tot;
e[tot].to=v;
e[tot].nxt=head[u];
head[u]=tot;
}
ll nvl[MAXN];
ll WtSn[MAXN],sz[MAXN],dfn[MAXN],did[MAXN],ID=0,cid[MAXN]/*这个是CHAIN ID, 即所属的链中的头部*/;
ll fa[MAXN],dep[MAXN];
void dfsInit(ll u,ll fath){
sz[u]=1;
WtSn[u]=0;
for (int i=head[u];i;i=e[i].nxt){
ll v=e[i].to;
if (v==fath){
continue;
}
fa[v]=u;
dep[v]=dep[u]+1;
dfsInit(v,u);
sz[u]+=sz[v];
if (sz[v]>sz[WtSn[u]]){
WtSn[u]=v;
}
}
}
void dfs(ll u,ll fath){
cid[u]=fath;
dfn[++ID]=u;
did[u]=ID;
if (!WtSn[u]) return;
dfs(WtSn[u],fath);
for (int i=head[u];i;i=e[i].nxt){
ll v=e[i].to;
if (v==WtSn[u] || did[v]){//嘿嘿嘿,did也要重置
continue;
}
dfs(v,v);
}
}
ll qpow(ll x,ll y){
ll tmp=1;
while (y){
if (y&1) tmp=tmp*x%MOD;
x=x*x%MOD,y>>=1;
}
return tmp;
}
struct Node{
ll val;
};
Node a[MAXN<<4];
#define lson (id<<1)
#define rson (id<<1|1)
#define mid ((l+r)>>1)
void pushup(ll id){
a[id].val=(a[lson].val+a[rson].val)%MOD;
}
void build(ll l,ll r,ll id){
if (l==r){
a[id].val=nvl[dfn[l]]*nvl[dfn[l]]%MOD;
return;
}
build(l,mid,lson);
build(mid+1,r,rson);
pushup(id);
}
void modify(ll L,ll R,ll l,ll r,ll id,ll k){
if (L<=l && r<=R){
a[id].val=k*k%MOD;
return;
}
if (L<=mid) modify(L,R,l,mid,lson,k);
if (mid+1<=R) modify(L,R,mid+1,r,rson,k);
pushup(id);
}
ll query(ll L,ll R,ll l,ll r,ll id){
if (L<=l && r<=R){
return a[id].val%MOD;
}
ll sum=0;
if (L<=mid) sum=(query(L,R,l,mid,lson)+sum)%MOD;
if (mid+1<=R) sum=(query(L,R,mid+1,r,rson)+sum)%MOD;
return sum;
}
#undef lson
#undef rson
#undef mid
ll T,cnt=0;
void Q_chain(){
ll u,v;
cin>>u>>v;
ll ans=0,len=0;
while (cid[u]!=cid[v]){
if (dep[cid[u]]<dep[cid[v]])
swap(u,v);
ans=(query(did[cid[u]],did[u],1,n,1)+ans)%MOD;
len+=(did[u]-did[cid[u]]+1);
u=fa[cid[u]];
}
if (dep[u]<dep[v]){
swap(u,v);
}
ans=(query(did[v],did[u],1,n,1)+ans)%MOD;
len+=did[u]-did[v]+1;
if (ans==len*(len+1)%MOD*(2*len+1)%MOD*qpow(6,MOD-2)%MOD)
cout<<"Yes"<<endl;
else
cout<<"No"<<endl;
}
void M_node(){
ll u,vl;
cin>>u>>vl;
modify(did[u],did[u],1,n,1,vl);
}
int main()
{
freopen("perm.in","r",stdin);
freopen("perm.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>T;
while (T--){
cin>>n>>m;
for (int i=1;i<=n;i++){
cin>>nvl[i];
}
for (int i=1;i<n;i++){
ll u,v;
cin>>u>>v;
add_edge(u,v);
add_edge(v,u);
}
dfsInit(1,0);
dfs(1,1);
build(1,n,1);
for (int i=1;i<=m;i++){
ll opt;
cin>>opt;
if (opt==1) Q_chain();
else M_node();
}
for (int i=1;i<=n;i++){
head[i]=0,WtSn[i]=0;
did[i]=0;
}
tot=0,ID=0;
}
}
所以说,真的什么时候都要树链剖分吗?
先考虑到将所有的情况离线下来,就是对于每一种颜色,起码保证这个时候时间复杂度还是一次函数的,剩下的还够支持一个对数。
这里看上去需要树链剖分,但因为一个颜色只会对儿子往上的路径有贡献,实际上用线段树或者树状数组去维护子树信息就可以了。
\(Tree\) \(Destruction\)
解:树的直径
mlk的一组题
对,直径就是我爸
首先,我们需要明白的是,直径ta真的很牛逼,一个点到所能到达的最远的点,一定在直径上,如果不是,那这个新找到的节点就可以顶替直径的其中一边独占一方,这样一来,我们只需要先找到直径,然后一次次从非直径的点按照拓扑的顺序去减去节点,最后再把直径删了即可。
\(Three\) \(Paths\) \(on\) \(a\) \(Tree\)
解: 同上
这个稍稍显然一些,选直径一定在其中,剩下的你只需要找所有叶子中离直径最远的一个就可以了。
如何理解?
我们考虑把整一条链(直径)拉下来,像鱼骨中间那一个一样,那么对于一定要选直径的方案而言,肯定就是找到下一个离直径最远的点,那如果我们不选呢?你可能会觉得其中两个“鱼鳍”连在一起再加上直径更优,但这种情况不存在,因为这个时候其中一个鱼鳍就会被并在直径上,思考下去就会发现任何方案要么被直径所包含,要么就是本质上不优秀。(比如下面的 \(9\) 本身就属于直径)