片集 - 思维（博弈论，构造，etc.） - 1

欢迎来看 “片” （的简介）

由于-\(看片\)-生涯转瞬即逝，于是我选择对“\(片\)”进行一定的总结：

相信你一定看懂了

由于开始的时间有一点晚，就姑且认为我以后会慢慢补充吧......

回到总部

\(P6970\) \([NEERC2016]\) \(Game\) \(on\) \(Graph\)

解：博弈论

首先，我们有更原始的问题：

\(A\), \(B\) 在 \(DAG\) van 游戏，二者都想赢，\(A\) 先手，问哪些点上有制胜策略

很简单，我们可以发现一个点与之相连的所有点种如果全都是必胜的，这个点就是必败点，反之，如果里面有必败点，那你肯定会把这个点留给后者，也就是必胜点。

实现方面类似拓扑排序，因为如果没有出度，那肯定是负，然后往上推就可以了，同时，注意一下要建反图。

回到原题，这里唯一的区别就是胜，平，负的顺序变了，我们把定义也改了，就行了，不过在此之前还要看一下平局的情况，因为这道题是可以有环段的。

首先平局就是那些不能被 \(0/1\) 定义，即胜负定义的点，那么非常简单，如果对于先手而言，如果子节点种有不确定的，那这个点就跟着不确定，即平，反之，对于后手而言，只有在全是平手的时候选择不确定，即平，其它依旧。

然而，我们都强调了，不确定不确定，但我们可以知道的是，对于先手而言，只要子节点有不确定的，就不确定，所以我们只需要确定 \(0/1\) 即可，剩余的全是平手。而对于后手而言，也可以通过只看 \(0/1\) 胜负来判定。于是平的情况就被解决了。

相信你一定已经开始写了，相信你也一定为实现感到困恼，不妨借鉴 (Ctrl+C,Ctrl+V 一下大佬的写法，复述一下他的做法：

题解中的 \(vis_{i,0/1}\) 在能判定一个点有没有被询问过的同时，还清楚的告诉了你它的答案，因为我们知道，对于 \(B\) （即题目中的 \(Georgiy\)）而言，只要它儿子中的所有节点有其中一个为负，则必然它会去取之并变成胜，所以将这一个点设为胜，反之对于 \(A\) （即题目中的 \(Gennady\)） 的情况，只有对于所有点被取完的时候才能这么做。

更细致地说，在 \(dfs\) 的过程中，要不断地交换当前的先后手情况，而 \(vis\) 在访问与否的意义下不变，然而在答案的意义下有所变化，对于先手为 \(A\) 而言，\(vis\) 为 \(1\) 是败，为 \(0\) 反倒是胜，而对于 \(B\) 而言就是反过来的，在第一次，以 \(A\) 为先手的 \(dfs\) 情况下，就可以把所有的答案为胜负的情况算出来，后者的 \(dfs\) 则可以把所有平手情况算出来。

如果你渐渐觉得混沌的话，记住最开始的意义：

1. \(0/1\) 就是 \(A/B\) 的先手情况；
2. \(0/1\) 对应的答案一个是 \(1\) 对负， 一个是 \(0\) 对胜；
3. 对于 \(1\) 而言，它的答案一定只有在其他的点都被访问过且都不再是为平的情况下且为胜的时候才能是 \(1\)， 而对于 \(0\) 的情况下，则只需要保证其中一个为 \(0\) 就可以为胜。

其他的思考：

1. 为什么遇到一个 \(A\) 就可以判定它一定是负？因为由于我们是 \(0/1\) 交错的，因此一旦遇到一个合法的 \(A\) 就能说明它周围一定是 \(B\)， 且全都是胜，故这一个 \(A\) 一定是负。

2. 为什么第一个 \(dfs\) 可以把所有的胜负情况全算出来？ 因为我们第一次 \(dfs\) 判断的就是 \(A\) 为先手负的情况和 \(B\) 为先手为胜的情况，两种情况在图上相互关联且不存在其它情况与之联系，所以说如果这样做就只会把这种情况找出来，那么就只会把上述情况找出来，又因为非胜即负或平，所以第二层循环只用把能否找到的情况判了，也就是判断是胜负还是平局。

\(AT\)\(agc002\)\(e\) \([AGC002E]\) \(Candy\) \(Piles\)

解：适当的画画，博弈

我们先把石子按从大到小的顺序排个序，如下图：

你一定以为我用的是 \(IOS\)，那你高估了 \(GF\) 的实力了

那我们的操作就变得有所规律了：

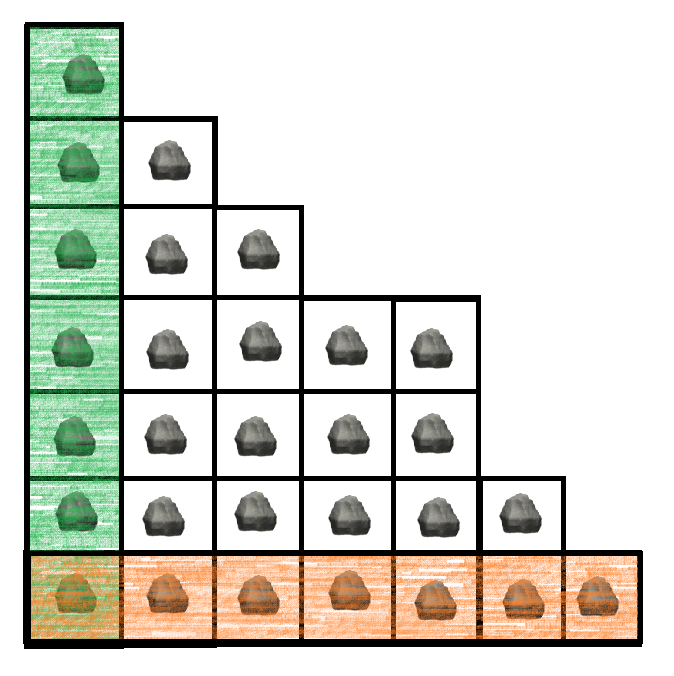
\(\textcolor{green}{绿}\)色就是操作 \(1\), \(\textcolor{orange}{橙}\)色就是操作 \(2\)，我们现在只观察左下角的石头，可以发现这样的操作相当于就是让一个 \(BOT\) 从左下角直走上和右不停地走到边缘的操作。我们知道最边缘的且无法操作的石头由于是最后一个所以一定是负，对于上和右两个石头只要有一个是负那当前这一个点就是胜，反之，只有当上和右两个石头都是胜的时候当前这个点才是负，于是从最外层往里面推，就有下面这个图 \(\textcolor{green}{绿}\)是胜，\(\textcolor{red}{红}\)是输：

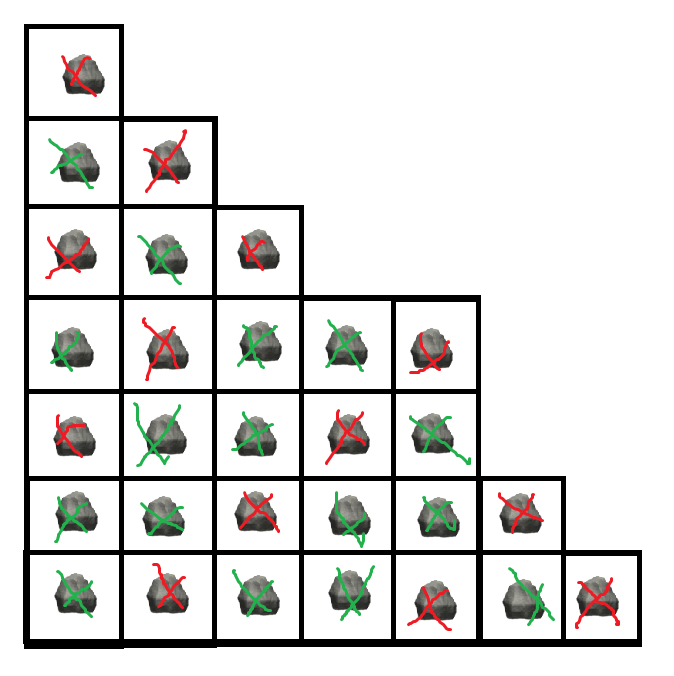
不难发现， 对角线上的值是相同的。

那我们就找到一左下角为顶点的最大正方形的右上角定点的胜负情况，可以发现它就是这个正方形的边长与边长对应下标的石子长度的差的奇偶情况和最长的与边长高度相同的以下一位为开头的前缀长度的奇偶情况的或。

注意一下如果没有合法的正方形的情况。

CF388C Fox and Card Game

解： 博弈论

这道题知道思路之后非常简单，所以写的也会很简单，但我觉得这个思路肯定非常实用且重要。

结论就是，对于多个人玩游戏时，若某个东西二者都能达到，那么两个人都会去争取，此时就会出现平分天下的局面，若问二者全职差距最小的情况时，若 \(a\) 多，那么 \(b\) 会努力争取更大的，反之亦然，因此，最小的就是两个都取到自己范围内的平分的情况。

放在这道题中，对于偶数情况，就是先手取左，右手取右。

奇数时考虑一下先后手，此时，先手就一定会去取较大中间权值，因此中间的所有书取出来排序后从大到小依次取就可以了。

类似的题：

\(CF794E\) \(Choosing\) \(Carrot\)

解：
多了个 \(k\) 的限制，在上一题相同取的基础上加一个对 \(k\) 的枚举即可，但这是 \(\mathcal{O}(n^2)\) 的，很简单 \(st\) 表或者线段树。

若感觉太麻烦，也可以递推地从奇偶的 \(k\) 从小往大找。

\(CF1991B\) \(AND\) \(Reconstruction\)

解：二进制基本运算，构造

马德，真服了，第一次打 \(CF\) 被程题干爆了，只能说我对二进制一窍不通。

以下内容纯属照搬 \(CF\) 官解

由于看题解的时候被下表搞得乱七八糟，先把题目中的 \(b_i\) 和 \(a_i\) 的的定义写一下：

\(b_i\) = \(a_i\) \(\&\) \(a_{i+1}\)

先说结论，构造 \(a_i\) = \(b_i\) \(|\) \(b_{i-1}\)，然后判定 \(a_i\) \(\&\) \(a_{i+1}\) 是否为 \(b_i\) 即可。

你一定觉得这很牛逼，但听着又好像很扯淡，下面开始证明：

首先 \(a_i\) \(\&\) \(a_{i+1}\) \(=\) \((b_i\) \(\&\) \(b_{i-1})\) \(|\) \((b_i\) \(\&\) \(b_{i+1})\) \(=\) \(b_i\) \(|\) \((b_{i-1}\) \(\&\) \(b_{i+1}\))

再根据定义，我们知道这个东西最开始是等于 \(b_i\) 的，所以看起来迎刃而解，然而这一条定义式是我们认为定义出来的，所以还需要进行验证，那么，顺着原本的目的去，为什么这个东西就是对的呢，由原式可知只有当存在 \(b_{i}\)中的一位是 \(0\)，\(b_{i-1}\)中相同的一位是 \(1\)，\(b_{i+1}\)相同的一位也是 \(1\) 时 \(a_i\) \(\&\) \(a_{i+1}\) 才会不等于 \(b_i\)，考虑再把原式放到这个有问题的一位（注意后面说的某个数等于1只是说这一位），也就是 \(b_i\) = \(a_i\) \(\&\) \(a_{i+1}\) ，那么由于 \(b_{i-1}\) 和 \(b_{i+1}\) 等于 \(1\)，所以，\(a_{i-1}\), \(a_i\), \(a_{i+1}\) 都等于 \(1\) 但又 \(b_i=0\) 所以说严重矛盾，最后考虑边缘的两个 \(a_i\)，这个时候它没有 \(b_{i-1}\) 或者 \(b_{i+1}\)自然就只需要把他们变成 \(0\) 即可，然后就完了……