片集 - 数学 - 1
欢迎来看 “片” (的简介)
由于-\(看片\)-生涯转瞬即逝,于是我选择对“\(片\)”进行一定的总结:
相信你一定看懂了
由于开始的时间有一点晚,就姑且认为我以后会慢慢补充吧......
回到总部
p.s. 这里容纳了各种各样有关数学的东西,包括组合数学,概率期望等一些列稀奇古怪的东西。
\(P7161\) [\(COCI2020\) \(-\) \(2021\)#\(2\)] \(Euklid\)
解:数学
\(GCD(a,b)=g\)
\(\implies a=g\times k1,b=g\times k2\)
\(R(a,b)=h\)
\(\implies\) \(a=h,b∈[h^k,2\times h^k)\)
\(\implies\) \(gk1=h,gk2∈[h^k,2\times h^k)\)
\(∵\) \(R(a,b)=R(gk1,gk2)\implies R(\lfloor \frac{k1}{k2} \rfloor,gk2)\) \(!!重点!!\)
\(\implies\) \(k1/k2=h,gk2∈[h^k,2\times h^k)\)
\(\implies\) \(k1/k2=h,k2∈[\lfloor \frac{h^k}{g} \rfloor,\lfloor 2 \times \frac {h^k}{g} \rfloor)\)
\(\implies\) \(k2∈[\lfloor \frac{h^k}{g} \rfloor,\lfloor 2 \times \frac {h^k}{g} \rfloor),k1=h \times k2\)
更具体的,k2直接去 $ \lceil \frac{h^k}{g} \rceil$, \(k1\) 要保证自己与 \(k2\) 互质,所以 \(k2\) 取 \(k1\times h+1\)
好吧,实际上这一系列上下取整让我感到非常不安,不过你可以自行检验一下 😕
\(P3214\) \([HNOI2011]\) \(卡农\)
解:排列组合,数学,计数
这是黑?????????????????????????????????????
首先,我们将每一种情况进行 “二进制拆分”,那么每一种音符可选可不选,那就是总共有 \(2^n-1\) 种情况,对于排列而言,我们只需要在求答案的时候除以一个 \(m!\) 即可, 实际上是由组合数做法的,但看到一半的时候被 \(xch\) 阻止了, 那么对于排列而言就有 \(\mathcal{A}_{2^n-1}^{i}\), 继续想一想,由于题目种中有出现个数为偶数的限制,所以在确定完 \(i-1\) 个的时候,第 \(i\) 个和声就呼之欲出了,因为如果对于一种音符起那面出现偶数次,那么这个和声中就不能加入这个音符,反之,如果是奇数次,那么这一次就必须加入,因此第 \(i\) 个和声在确定完前面的和声就可以唯一确定了,所以就拍出了一些没用的情况,并且加上了偶数次的限制,这个时候方案数变成了 \(\mathcal{A}_{2^n-1}^{i}\)。
现在继续来考虑其他限制,对于不能存在空集的情况就是上述 \(m-1\) 的时候发现每一个音符都出现了偶数次,这个时候定义 \(f_i\) 表示前 \(i\) 组和声的方案数,这个时候多余的情况就是 \(f_{i-1}\)。
继续考虑,对于不能有相同的和声的情况,钦定存在 \(i\), \(j\) 它们相同,这个时候剩余的 \(i-2\) 组和声构成的卡农就是合法的,也就是 \(f_{i-2}\), 这个时候看 \(i\) 由于现在规定它要合法,所以就有 \(2^n-1-(i-2)\) 种情况,附加上 \(j\) 的位置枚举,也就是 \(i-1\),就有这种情况的排除办法 \(f_{i-2} \times (i-1) \times (2^n-1-(i-2))\)。
最后就有递推式:
\(f_i=\mathcal{A}_{2^n-1}^{i}-f_{i-1}-f_{i-2} \times (i-1) \times (2^n-1-(i-2))\)
p.s 注意排列是 \(\frac{n!}{(n-m)!}\) 不是 \(\frac{n!}{m!}\),别当郝精锐了
\(CF451E\) \(Devu\) \(and\) \(Flowers\)
解:计数,排列组合,容斥,数学
不难发现,我的数学真的像依托勾石。
分开讲一下这道题涉及到的两个点。
首先,这个稍稍独特一点的插板,只是我没见过插板还能加的。
暂且不考虑 \(f_i\) 的约束
现在最开始有 \(s+1\) 个位置插板,共有 \(n-1\) 个板,考虑插板。
开头跟普通的插板一样,只是由于这次你能在已有的板两边都差一个板,于是就有方案(不考虑重复):
$(s+1) \times (s+2) \times \dots \times (s+n-1) $
也就是
\(\frac{(s+n-1)!}{s!}\)
又因为我们要求的是组合的情况,得到的却是排列,所以套路的除以一下板子的插入位置 \((n-1)!\)
那就有了最终的方案数:
\(\frac{(s+n-1)!}{s!(n-1)!}=\mathcal{C}_{s+n-1}^{n-1}\)
接下来是容斥
好吧,我觉得这东西性感理解跟理性理解的效果相同。
就是奇偶对应正负,不断地加减对应的的 \(|s_i|\) 就好了。
So?
接下来我们从最开始的简单插板入手此时的方案数就是 \(\mathcal{C}_{s+n-1}^{n-1}\),显然,这个时候我们压根没有想 \(f_i\) 我们考虑容斥一下,先从单一的一种花说起,我们现在钦定它已经选了超过 \(f_i\) 个,那么就是在原本的 \(s+n-1\) 个空格少了变为 \(s+n-1-(f_i+1)\) 而插得板相同。
这里为什么就可以保证吧大于 \(f_i+1\) 的情况考虑进来呢,因为我们这次插的板的个数不变,因此仍有可能把板插在当前 \(i\) 的位置。
同理,扩张到多个 \(i\),就可以有 \(\mathcal{C}_{n+s- \sum_{k} f_i-(k+1)}^{n-1}\)
后面就很简单了,普通的容斥。
\(CF1924D\) \(Balanced\) \(Subsequences\)
解:卡特兰数,计数,排列组合
仅以此片题解来说服自己关于卡特兰数的东西。
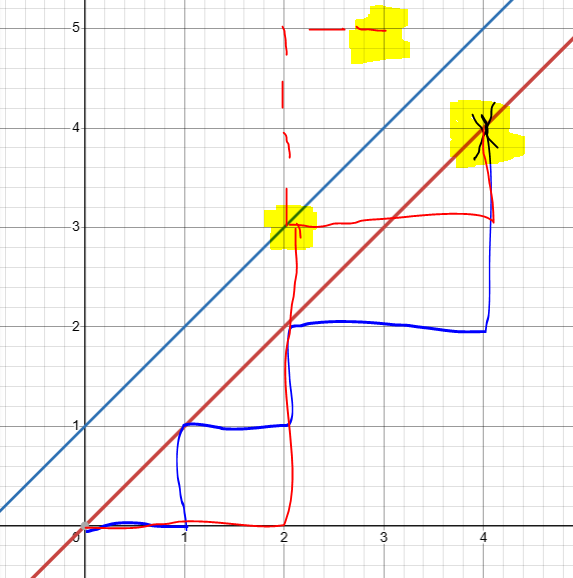
图很丑但不费事了
背景就是我们要从 \((0,0)\) 只向上、向左跑到到 $ (n,n) $ 问不超出 \(y=x\) 时的方案数。
不考虑限制 \(y=x\) 从 \((0,0)\) 跑到 \((n,n)\) 共有 \(2 \times n\) 次抉择,选了其中一个方向剩余的就清楚了,所以共有 \(\mathcal{C}_{2\times n}^n\) 的方案数。
现在容斥,考虑超过 \(y=x\) 的情况,有一种牛逼的操作就是把超过 \(y=x\) 的线以 \(y=x+1\) 为对称轴对称,如上图的虚线部分,可以发现,所有这样的线都会经过 \((n-1,n+1)\) 的点,因此非法方案就有 \(\mathcal{C}_{2\times n}^{n-1}\) 是不是想着就很奇怪,那就算是合法的情况对称完不也是一定经过 \((n-1,n+1)\)。
这就是对合法方案的理解不透彻,它们的根本不同之处就是其中一个经过了 \(y=x+1\), 是因为经过了所以才有对称操作的,或者说如果不是因为经过 \(y=x+1\),那所有线多直接对称,此时,火兔就能发现所有线都仍然是最开始的 \(n \times n\) 的方格只不过形状变了。
我不知道这合不合理,纯粹自己扯出来的。
最后合法方案数就是二者的差:
\(\mathcal{C}_{2\times n}^{n}-\mathcal{C}_{2\times n}^{n-1}\)
这就是我一直半懂不懂的卡特兰数了……
放到这道题中,在之前的题目中我们了解到一个关于括号匹配问题的结论,就是若把左括号的权值设为 \(1\),有括号的权值设为 \(-1\) 则他的每一位的前缀和大于等于 \(0\),现在把这个结论跟卡特兰融合一下,那么我们让左括号设为向左走,右括号设为向上走,那只要每一次行走不超过过 \(y=x\) 即可。
接下来考虑左右括号的限制 \(n\) 和 \(m\),看一看题目,发现由于最多有 \(2 \times k\) 个括号匹配,那么剩余的括号一定组成连续的右括号和连续的左括号例如 \()))))))))))))))))((((((((((\) 这样的东西,我们可以枚举左括号右括号合起来的地方前有 \(i\) 个匹配的括号时(后面称这个地方为关键位置)的方案,回到那张卡特兰数的图上,有括号共有 \(m\) 个,现在为止匹配好的共有 \(i\) 个,那么后面还要用 \(k-i\) 个,所以在关键位置时用了 \(m-k+i\) 个,又因为我们钦定了最后一位是右括号,所以只用到达 \((i,m-k+i-1)\) ,最后一位固定,那相应的它的方案数套一下公式就是
\(\mathcal{C}_{2\times i+m-k-1}^{i}-\mathcal{C}_{2\times i+m-k-1}^{i-1}\)
类似的左括号是一样的只不过最后一位就不用考虑了,答案是
\(\mathcal{C}_{2\times (k-i)+n-k}^{k-i}-\mathcal{C}_{2\times (k-i)+m-k-1}^{k-i}\)
注意一下边界每一个到小于等于 \(0\)的时候要特判,枚举 \(i\),输出,结束了!!!!!!!!
是吗???
好吧,还有跟简单的
我们简单点想,直接 \(n \times m\) 的方格,不超过 \(y=x\) 即可,那就直接把卡特兰糊了。
[\(ABC160F\)] \(Distributing\) \(Integers\)
解:树上问题,计数
因为帽的请求,来温“故”知新,发现之前我就是个傻子,\(\mathcal{C}\) 完就跑。
具体的树上跳来跳去就不讲了,我认为这道题关键就在与它的数学思维。
由题知,一个父亲一定先被覆盖,然后才是它的儿子,我们考虑一个二元链,假设整棵树就他俩,方案是多少?
咳咳,写成"代数"形式,实际上是:
神么意思呢,就是总方案数乘上它对应的比例,二元链比较典型,可以发现就是就是它的 \(\text{size}\) 的所有方案乘上不包括它自己的大小的阶乘(它儿子的方案),也就是这个节点作为一个序列开头的方案。
赞数不考虑它儿子是否合法,答案就是 \(\large\frac{1}{sz_{u}}\) 乘上对应的方案数,如果考虑它的儿子的话,可以发现每一个儿子都有它的 \(\large\frac{1}{sz_{son_u}}\) 也就是一坨儿子大小相乘再乘上它自己,此时乘上对应的方案数才是真正合法的答案。
二维图形的一些问题
咳咳,我知道,这里原本只应存在题目,但最近有点寂寞,想爽一爽,于是找来依托看起来像对恶臭的石:
当然,凸包只是一小部分。
先介绍一些概念:
对踵点: 在凸包上画上一对平行线,呐,它们就是一对对踵点。
额,暂时就这些了。
接下来,有一些必要的数学“常识”
定义: $$|a \times b|=|a||b| sin θ$$
那么具体证明呢?经过炮夕的讲解,我懂了!!!!!!
证明:
令两个向量为 \(a=x_1 i+y_1 j\),\(b=x_2 i+y_2 j\),由于向量叉乘的分配律,把这两坨屎合在一起就得到了 \(x_1 x_2 i \times j + x_1 y_2 i \times j + x_2 y_1 j \times i + y_1 y_2 i \times j\)
由于 \(i \times i\) 和 \(j \times j\) 都等于 \(0\),而 \(i \times j\) 等于 \(+k\),反之为 \(-k\)
所以最终话捡出来的形式就是 $$(x_1y_2-x_2y_1)k$$由定义式,你就有新的结论了 \(|a||b|sinθ=x_1y_2-x_2y_1\),也就是 \(a\) 和 \(b\) 形成的平行四边形就是 \(x_1y_2-x_2y_1\),只能说太帅了
把单位向量除去,只看模长可以发现这样算出来的结果除以 \(2\) 就是 \(\triangle OAB\) 的面积,于是,我们进行旋转凸壳就有了媒介,当然我们要先了解凸包。
\(二维凸包\)
解: ~
一切的一切起源于此……
这么多个点,当然选择一个基准拓展是一个不错的主意,可以发现,\(y\) 坐标最小的点一定在凸包上,于是,我们将这个点定位原点 \(O\)。
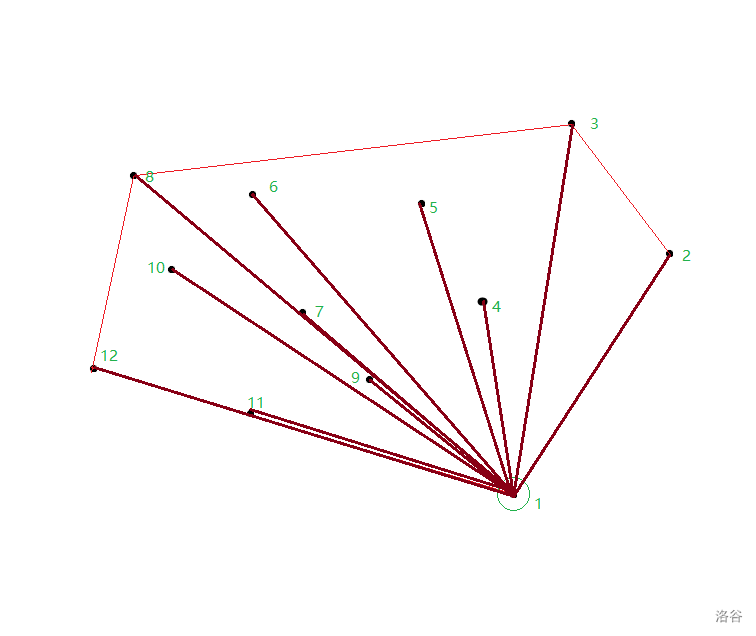
正如上图中的 \(1\) 号点。
我们依次进行一些算法的讲解,
首先是最暴力的办法,从原点开始不断地找能将其他的全都放在一侧的点,算法复杂度 \(\mathcal{O}(nm)\) ,\(m\) 为凸包上点的数目,这种算法被叫做 \(Jarvis\),钢铁侠折了
中间还有一些大同小异的暴力,在这道题的题解中有很多,我就不逼了,现在,就直接讲讲这个所谓的高级算法
像上面那个图,我们可以选择按照一定的基准进行排序,可以发现,类似斜率的东西是一个不二的选择,然而斜率是越靠近 \(y\) 轴越大,所以实际上应该是 \(\frac{x}{y}\) 从大到小排序,或者说,用某个更高级的说法——极角
然后我们开始适当模拟,发现一个绝妙的办法,用栈依次记录每一个凸包上的点,每一次发现拐弯的时候就不停地退栈直到不拐弯为止,什么叫拐弯呢,参考下图的\(3\), \(4\)线段就是一个拐弯,于是我们用 \(5\) 覆盖 \(3\),\(4\),即退掉 \(4\) 点。
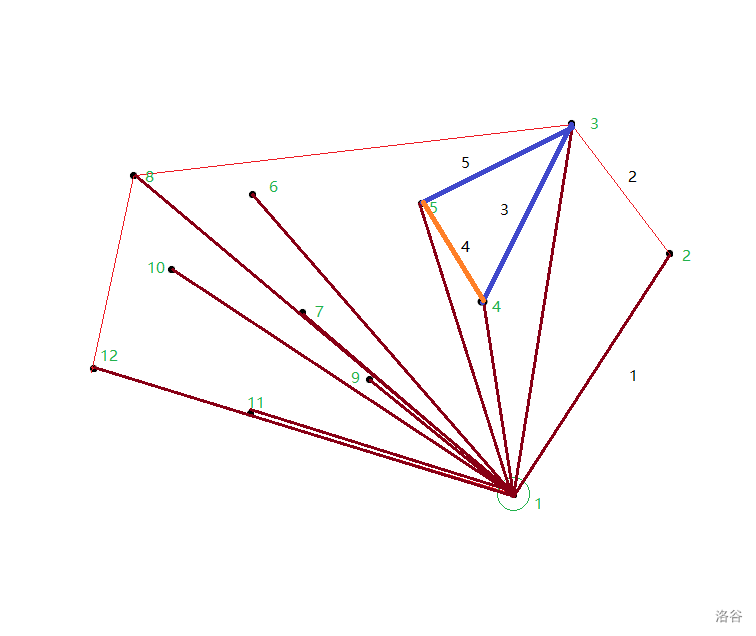
如此操作下去,根据经验而言,你就得到了最终的凸包,哈哈哈哈哈哈哈哈哈哈哈哈
怎么证明?
暂时看到一些证明都是用语言表述而来的,并没有看到谁用数学语言严格形式的证明,所以我也来逼一点我的拙见,可以发现第一次早操作时,所形成的凸包就是第一个、二个点的时候所形成的凸包就是正确的凸包,每一次加入一个点本质就是在扩大的操作,这么不断的操作,由于第一次操作无误,后续若干次操作也都不会有问题。这个算法叫做 \(Graham\)
点击查看代码
#include <iostream>
#include <map>
#include <algorithm>
#include <cmath>
#include <iomanip>
#define ll long long
using namespace std;
const int MAXN=1e5+5;
struct PoInTs{
double x,y;
};
PoInTs a[MAXN];
ll n,tot=0,lp,tp=0;
PoInTs stk[MAXN];
map <pair<double,double>,bool> mp;
long double ans=0.0;
bool cmp(PoInTs x,PoInTs y){
if (x.x*y.y==y.x*x.y){
if (x.y==y.y) return x.x<y.x;
return x.y<y.y;
}
return x.x*y.y>x.y*y.x;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n;
lp=1;
for (int i=1;i<=n;i++){
double x,y;
cin>>x>>y;
if (mp[make_pair(x,y)]) continue;
mp[make_pair(x,y)]=1;
a[++tot]={x,y};
if (a[tot].y<a[lp].y) lp=tot;
else if (a[tot].y==a[lp].y && a[tot].x<a[lp].x) lp=tot;
}
swap(a[lp].x,a[1].x);
swap(a[lp].y,a[1].y);
for (int i=2;i<=tot;i++){
a[i].x-=a[1].x;
a[i].y-=a[1].y;
}
a[1].x=0,a[1].y=0;
sort(a+2,a+1+tot,cmp);
stk[++tp]=a[1];
for (int i=2;i<=tot;i++){
while (tp>1 && (1.0*a[i].x-1.0*stk[tp].x)*(1.0*stk[tp].y-1.0*stk[tp-1].y)>=(1.0*stk[tp].x-1.0*stk[tp-1].x)*(1.0*a[i].y-1.0*stk[tp].y)) --tp;
stk[++tp]=a[i];
}
stk[++tp]=a[1];
for (int i=2;i<=tp;i++) ans+=sqrt(1.0*(stk[i].x-stk[i-1].x)*(stk[i].x-stk[i-1].x)+1.0*(stk[i].y-stk[i-1].y)*(stk[i].y-stk[i-1].y));
cout<<setprecision(2)<<fixed<<ans;
}
\(旋转卡壳\)
解:如上
首先用上面的算法求出凸包大小。
接着,像上面所说的对踵点,我们可以找一条破线段的对踵点,如此一来,你发现你要是以一种方向(顺、逆时针)单调移动,你发现对应的对踵点也是以同样方向移动的,那这样一来不就是一个单调的问题吗?
于是,牛逼双指针成功了\(\mathcal{O}(n)\),瓶颈在上面的算法中的对数。
关键核心代码(把这一段接在上面就是这道题)
n=tp;
ans=getlen(stk[1],stk[2]);
if (n==2){
cout<<ans;
return 0;
}
ll j=2;//从2开始不会劣,3可能有所疏漏
long double tmp=0;
stk[n+1]=stk[1];
for (int i=1;i<=n;i++){
tmp=0;
while (gettgl(stk[i],stk[i+1],stk[j])>=tmp){
tmp=gettgl(stk[i],stk[i+1],stk[j]);
++j; if (j>n) j-=n;
}
--j; if (j==0) j=n;//注意要复位
ans=max(max(getlen(stk[i],stk[j]),getlen(stk[i+1],stk[j])),ans);
}
\(凸包面积\)
学完这些之后,你信誓旦旦地以为自己可以求什么多边形面积了,可你发现自己是个超级大小丑,因为很小的时候,你就学了"迪克"(毕克)定理,哈哈哈哈哈哈哈哈哈哈哈哈
咳咳,或者,为了不显得你输得这么惨,你完全可以依靠叉积并运用已算出的凸包,并定同样的原点作为原点,然后逆时针不停的用叉积,ok,完了~,时间复杂度依然十分优秀,瓶颈依然在于排序。放一些有用的子函数吧。
点击查看代码
long double gettgl(PoInTs x,PoInTs y,PoInTs o){//叉积,并以 o 为原点
x.x-=o.x;
y.x-=o.x;
x.y-=o.y;
y.y-=o.y;
return abs(x.x*y.y-y.x*x.y);
}
long double getlen(PoInTs x,PoInTs y){//两点距离公式
return (x.x-y.x)*(x.x-y.x)+(x.y-y.y)*(x.y-y.y);
}
Tips
- 组合数预处理的时候 \(fac_0\) 和 \(inv_0\) 都要为 \(1\)



