2019-7-22 考试总结
A. 方程的解
$exgcd$,然后一堆特判,我分了$27$种情况,有些情况可以合并。
统计个数的时候,我们知道它的通解$X=X_0+k\times \frac{b}{gcd}$,$Y=Y_0-k\times \frac{a}{gcd}$,
然后我们让它们分别大于$0$,得到$k_1>=\frac{-X_0}{\frac{b}{gcd}}$,$k_2<=\frac{Y_0}{\frac{a}{gcd}}$,
我也不知道要怎么取整。反正判断一下就好了,最后数目就是$k_2-k_1+1$,
丑陋的代码:

#include<iostream> #include<cstring> #include<cstdio> #include<cmath> #define Reg register using namespace std; int t; long long exgcd(long long a,long long b,long long &x,long long &y) { if(b==0) {x=1; y=0; return a;} long long d=exgcd(b,a%b,x,y); long long tmp=x; x=y; y=tmp-(a/b)*y; return d; } long long gcd(long long x,long long y) { if(y==0) return x; else return gcd(y,x%y); } int main() { scanf("%d",&t); while(t--) { long long a,b,c,x,y; scanf("%lld%lld%lld",&a,&b,&c); if(a>0&&b>0&&c==0) printf("0\n"); else if(a>0&&b>0&&c<0) printf("0\n"); else if(a>0&&b==0&&c>0) { if(c%a==0) printf("ZenMeZheMeDuo\n"); else printf("0\n"); } else if(a>0&&b==0&&c==0) printf("0\n"); else if(a>0&&b==0&&c<0) printf("0\n"); else if(a>0&&b<0&&c>0) { int p=gcd(a,-b); if(c%p==0) printf("ZenMeZheMeDuo\n"); else printf("0\n"); } else if(a>0&&b<0&&c==0) printf("ZenMeZheMeDuo\n"); else if(a>0&&b<0&&c<0) { int p=gcd(a,-b); if((-c)%p==0) printf("ZenMeZheMeDuo\n"); else printf("0\n"); } else if(a==0&&b>0&&c>0) { if(c%b==0) printf("ZenMeZheMeDuo\n"); else printf("0\n"); } else if(a==0&&b>0&&c==0) printf("0\n"); else if(a==0&&b>0&&c<0) printf("0\n"); else if(a==0&&b==0&&c>0) printf("0\n"); else if(a==0&&b==0&&c==0) printf("ZenMeZheMeDuo\n"); else if(a==0&&b==0&&c<0) printf("0\n"); else if(a==0&&b<0&&c>0) printf("0\n"); else if(a==0&&b<0&&c==0) printf("0\n"); else if(a==0&&b<0&&c<0) { b=-b,c=-c; if(c%b==0) printf("ZenMeZheMeDuo\n"); else printf("0\n"); } else if(a<0&&b>0&&c>0) { int p=gcd(-a,b); if(c%p==0) printf("ZenMeZheMeDuo\n"); else printf("0\n"); } else if(a<0&&b>0&&c==0) printf("ZenMeZheMeDuo\n"); else if(a<0&&b>0&&c<0) { int p=gcd(-a,b); if((-c)%p==0) printf("ZenMeZheMeDuo\n"); else printf("0\n"); } else if(a<0&&b==0&&c>0) printf("0\n"); else if(a<0&&b==0&&c==0) printf("0\n"); else if(a<0&&b==0&&c<0) { a=-a,c=-c; if(c%a==0) printf("ZenMeZheMeDuo\n"); else printf("0\n"); } else if(a<0&&b<0&&c>0) printf("0\n"); else if(a<0&&b<0&&c==0) printf("0\n"); else { if(a<0&&b<0&&c<0) a=-a,b=-b,c=-c; long long d=exgcd(a,b,x,y); if(c%d!=0) {printf("0\n"); continue;} long long x0=x*(c/d),y0=y*(c/d); //通解 x=x0+k*(b/d),y=y0-k*(a/d); //k>k1,k<k2; long long l1=b/d,l2=a/d; long long k1=(-x0)/l1,k2=y0/l2; if(y0-k2*l2<=0) --k2; if(y0-(k2+1)*l2>0) ++k2; if(x0+k1*l1<=0) ++k1; if(x0+(k1-1)*l1>0) --k1; if(k2-k1+1<0) printf("0\n"); else if(k2-k1+1>65535) printf("ZenMeZheMeDuo\n"); else printf("%lld\n",k2-k1+1); } } return 0; }
B. visit
定义向上走的步数为$a$,向下走的步数为$b$,向右走的步数为$c$,向左走的步数为$d$,
那么$a-b=n$,$c-d=m$,$a+b+c+d=t$,
枚举$a$,$b、c、d$都可以确定,
那么我们确定了这走的步数,那么我们只需要用一个组合数。
$ans=\sum \limits_{a=n}^{a,b,c,d>=0} C_t^a \times C_{t-a}^b \times C_{t-a-b}^c \times C_{t-a-b-c}^d$,
模数是质数的可以直接$Lucas$,不是质数的要用$CRT$。
关于$Lucas$:
一开始不明白为什么小的质数为啥一定要用$Lucas$,经过$Lrefrain$大佬的指点稍微明白了一些,
如果一个模数是质数并且它很小,小到比$C_n^m$中的$n$和$m$还小的话,
求组合数的公式是$C_n^m=\frac{n!}{m!(n-m)!}$,
那么$n!$中肯定包含模数$p$,也就是$n!\% p=0$,$m!\% p=0$,
$\frac{n!}{m!}$那肯定是$0$,也就是说如果不用$Lucas$,那么我们求出来的解是$0$,但实际并不是这样。
如果$(t-n-m)\% 2!=0$,那么他不可能到达终点。
丑陋的代码:

#include<iostream> #include<cstring> #include<cstdio> #include<cmath> #define Maxn 100050 #define C(x,y,p) ((JC[p][x]*NY[p][y]%fen[p]*NY[p][(x)-(y)]%fen[p])%fen[p]) #define min(x,y) ((x)<(y)?(x):(y)) #define LL long long #define Reg register using namespace std; LL T,N,M,P,JC[50][Maxn],NY[50][Maxn],JPP[50],fen[50],LSS[50]; LL mi(LL x,LL y,LL p) { LL ans=1,base=x; while(y) { if(y&1) ans=(ans*base)%p; base=(base*base)%p; y>>=1; } return ans; } LL exgcd(LL a,LL b,LL &x,LL &y) { if(b==0) {x=1; y=0; return a;} LL d=exgcd(b,a%b,x,y); LL tmp=x; x=y; y=tmp-(a/b)*y; return d; } LL Lucas(LL x,LL y,LL p) { if(x<y) return 0; if(y==0||x==y) return 1; return (C(x%fen[p],y%fen[p],p)*Lucas(x/fen[p],y/fen[p],p))%fen[p]; } void CRT(LL a,LL b,LL c,LL d) { for(Reg int i=1;i<=fen[0];++i) { LL lss=Lucas(T,a,i) *Lucas(T-a,b,i)%fen[i] *Lucas(T-a-b,c,i)%fen[i]; LSS[i]=(LSS[i]+lss); } return; } int main() { scanf("%lld%lld%lld%lld",&T,&P,&N,&M); if(N<0) N=-N; if(M<0) M=-M; LL lss=P; for(Reg int i=2;i<=sqrt(lss);++i) { if(lss%i==0) { lss/=i; fen[++fen[0]]=i; } } if(lss>1) fen[++fen[0]]=lss; for(Reg int i=1;i<=fen[0];++i) { LL A,B; exgcd(P/fen[i],fen[i],A,B); A=(A%fen[i]+fen[i])%fen[i]; JPP[i]=A; JC[i][0]=NY[i][0]=1; for(Reg int j=1;j<=min(fen[i],T);++j) { JC[i][j]=(JC[i][j-1]*j)%fen[i]; NY[i][j]=mi(JC[i][j],fen[i]-2,fen[i]); } } LL ans=0; if((T-N-M)%2!=0||T<(N+M)) {printf("0"); return 0;} for(Reg int i=N;i<=T-M;++i) { LL a=i,b=a-N,c=(T+N+M-2*a)/2,d=c-M; if(a<0||b<0||c<0||d<0) break; CRT(a,b,c,d); } for(Reg int i=1;i<=fen[0];++i) ans=(ans+JPP[i]*P/fen[i]*LSS[i]); printf("%lld",(ans%P+P)%P); return 0; }
$wd$大神博客 传送门
C. 光
模拟暴力可拿60分。
说正解,对于每个格子,它只能走两条对角线的其中一条,
对每一个对角线编号,把它上边的障碍全记下来,可以用一个$vector$,
然后分四种情况分别讨论。
对于每种情况,我们找离他最近的障碍的坐标,然后接着分情况讨论,
注意的是如果他出现了像这种情况:
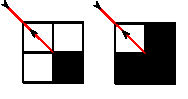
那么肯定要把这条光线折回到起点。
对于更新能到达的格子的数量,可以直接用较大的$x$坐标减去较小的$x$坐标,
如果它弹回到了起点,我们肯定要把$ans$减去$1$,
最后如果它弹回到了起点,那么我们判终止的条件应该是起点经过$2$次,
如果它没有回弹,那么判终止的条件应该是起点经过$1$次。
注意这个题有一个**测试点,它没有障碍,并且$n$和$m$的范围都特别大(导致我$RE$),
最后$QJ$过去了。。
丑陋的代码:

#include<algorithm> #include<iostream> #include<cstring> #include<cstdio> #include<string> #include<vector> #include<cmath> #include<map> #define abs(x) ((x)<0?(-1*(x)):(x)) #define max(x,y) ((x)>(y)?(x):(y)) #define Maxn 100050 #define Reg register using namespace std; struct Node {int x,y;}; int maxx,tp,n,m,k,tot,stx,sty,stk,stkf; long long ans; vector<vector<Node> > stop1(Maxn*20),stop2(Maxn*20); map <pair<int,int>,bool> num; map <pair<int,int>,short>vis; int pos(int x,int y,int kind) { if(kind==1||kind==2) { if(x<=y) { maxx=max(maxx,y-x); return y-x; } else { maxx=max(maxx,x-y+m+n+1); return x-y+m+n+1; } } else { maxx=max(maxx,x-y); return x+y; } } bool comp(Node a,Node b) {return a.x<b.x;} bool judge(int x,int y,int now,int pos,int kind) { if(kind==1) { if(stop1[pos][now].x>x&&stop1[pos][now].y>y) return 1; else return 0; } else if(kind==2) { if(stop1[pos][now].x<x&&stop1[pos][now].y<y) return 1; else return 0; } else if(kind==3) { if(stop2[pos][now].x>x&&stop2[pos][now].y<y) return 1; else return 0; } else if(kind==4) { if(stop2[pos][now].x<x&&stop2[pos][now].y>y) return 1; else return 0; } return 0; } Node erfen(int x,int y,int l,int r,int pos,int kind,int cnt) { // cout<<x<<' '<<y<<' '<<l<<' '<<r<<endl; if(l>=r||cnt>=25) { if(kind==1) { if(judge(x,y,r-1,pos,kind)) return stop1[pos][r-1]; else return stop1[pos][l-1]; } else if(kind==2) { if(judge(x,y,l-1,pos,kind)) return stop1[pos][l-1]; else return stop1[pos][r-1]; } else if(kind==3) { if(judge(x,y,r-1,pos,kind)) return stop2[pos][r-1]; else return stop2[pos][l-1]; } else { if(judge(x,y,l-1,pos,kind)) return stop2[pos][l-1]; else return stop2[pos][r-1]; } } int mid=(l+r)/2; if(judge(x,y,mid-1,pos,kind)) { if(kind==1) return erfen(x,y,l,mid,pos,kind,cnt+1); else if(kind==2) return erfen(x,y,mid,r,pos,kind,cnt+1); else if(kind==3) return erfen(x,y,l,mid,pos,kind,cnt+1); else if(kind==4) return erfen(x,y,mid,r,pos,kind,cnt+1); } else { if(kind==1) return erfen(x,y,mid,r,pos,kind,cnt+1); else if(kind==2) return erfen(x,y,l,mid,pos,kind,cnt+1); else if(kind==3) return erfen(x,y,mid,r,pos,kind,cnt+1); else if(kind==4) return erfen(x,y,l,mid,pos,kind,cnt+1); } } void dfs(int x,int y,int kind) { if(tp&&vis[make_pair(x,y)]) { if(vis[make_pair(x,y)]&&x!=stx&&y!=sty) return; if(vis[make_pair(x,y)]>=2) return; --ans; } if(!tp) { if(vis[make_pair(x,y)]) return; } tp=0; ++vis[make_pair(x,y)]; Node nex; if(kind==1||kind==2) nex=erfen(x,y,1,stop1[pos(x,y,kind)].size(),pos(x,y,kind),kind,0); else nex=erfen(x,y,1,stop2[pos(x,y,kind)].size(),pos(x,y,kind),kind,0); int x0=nex.x,y0=nex.y; if(kind==1) { pair<int,int> ls1,ls2; ls1.first=x0-1,ls1.second=y0; ls2.first=x0,ls2.second=y0-1; if(num[ls1]&&num[ls2]) { ans+=abs(x0-x); tp=1; dfs(stx,sty,stkf); } else if(num[ls1]&&!num[ls2]) { ans+=abs(x0-x); dfs(x0,y0-1,3); } else if(!num[ls1]&&num[ls2]) { ans+=abs(x0-x); dfs(x0-1,y0,4); } else if(!num[ls1]&&!num[ls2]) { ans+=abs(x0-x); tp=1; dfs(stx,sty,stkf); } } else if(kind==2) { pair<int,int> ls1,ls2; ls1.first=x0+1,ls1.second=y0; ls2.first=x0,ls2.second=y0+1; // cout<<x<<' '<<y<<' '<<kind<<' '<<stop1[pos(x,y,kind)][0].x<<' '<<stop1[pos(x,y,kind)][1].y<<" -next->"<<x0<<' '<<y0<<' '<<num[ls1]<<" "<<num[ls2]<<endl; if(num[ls1]&&num[ls2]) { ans+=abs(x-x0); tp=1; dfs(stx,sty,stkf); } else if(num[ls1]&&!num[ls2]) { ans+=abs(x-x0); dfs(x0,y0+1,4); } else if(!num[ls1]&&num[ls2]) { ans+=abs(x-x0); dfs(x0+1,y0,3); } else if(!num[ls1]&&!num[ls2]) { ans+=abs(x-x0); tp=1; dfs(stx,sty,stkf); } } else if(kind==3) { pair<int,int> ls1,ls2; ls1.first=x0-1,ls1.second=y0; ls2.first=x0,ls2.second=y0+1; if(num[ls1]&&num[ls2]) { ans+=abs(x0-x); tp=1; dfs(stx,sty,stkf); } else if(num[ls1]&&!num[ls2]) { ans+=abs(x-x0); dfs(x0,y0+1,1); } else if(!num[ls1]&&num[ls2]) { ans+=abs(x-x0); dfs(x0-1,y0,2); } else if(!num[ls1]&&!num[ls2]) { ans+=abs(x0-x); tp=1; dfs(stx,sty,stkf); } } else { pair<int,int> ls1,ls2; ls1.first=x0+1,ls1.second=y0; ls2.first=x0,ls2.second=y0-1; if(num[ls1]&&num[ls2]) { ans+=abs(x-x0); tp=1; dfs(stx,sty,stkf); } else if(num[ls1]&&!num[ls2]) { ans+=abs(x0-x); dfs(x0,y0-1,2); } else if(!num[ls1]&&num[ls2]) { ans+=abs(x0-x); dfs(x0+1,y0,1); } else if(!num[ls1]&&!num[ls2]) { ans+=abs(x-x0); tp=1; dfs(stx,sty,stkf); } } return; } int main() { // freopen("ray8.in","r",stdin); scanf("%d%d%d",&n,&m,&k); for(Reg int i=1,x,y,z;i<=k;++i) { scanf("%d%d",&x,&y); Node p; p.x=x; p.y=y; stop1[pos(x,y,2)].push_back(p); stop2[pos(x,y,4)].push_back(p); num[make_pair(x,y)]=1; } for(Reg int i=0;i<=m+1;++i) { Node p; p.x=0,p.y=i; stop1[pos(0,i,2)].push_back(p); stop2[pos(0,i,4)].push_back(p); p.x=n+1,p.y=i; stop1[pos(n+1,i,2)].push_back(p); stop2[pos(n+1,i,4)].push_back(p); num[make_pair(0,i)]=num[make_pair(n+1,i)]=1; } for(Reg int i=0;i<=n+1;++i) { Node p; p.x=i,p.y=0; stop1[pos(i,0,2)].push_back(p); stop2[pos(i,0,4)].push_back(p); p.x=i,p.y=m+1; stop1[pos(i,m+1,2)].push_back(p); stop2[pos(i,m+1,4)].push_back(p); num[make_pair(i,0)]=num[make_pair(i,m+1)]=1; } for(Reg int i=0;i<=n+m+n+m;++i) { sort(stop1[i].begin(),stop1[i].end(),comp); sort(stop2[i].begin(),stop2[i].end(),comp); } scanf("%d%d",&stx,&sty); string lss; cin>>lss; if(lss=="SW") stk=3,stkf=4; if(lss=="NE") stk=4,stkf=3; if(lss=="SE") stk=1,stkf=2; if(lss=="NW") stk=2,stkf=1; if(n==91432&&m==96962&&k==0) printf("8865429584"); else { dfs(stx,sty,stk); printf("%lld",ans); } return 0; }
$wd$大神博客 传送门
总结:
这次考试感觉脑子不对劲。。。
上来先看$T1$,一个$exgcd$的板子?
$20$分钟打了一个暴力,然后推了一个小式子,开始没对拍,考试还剩$1$个小时的时候打了一个对拍。
发现了很多错误,加了一堆特判。。最后还是没加够。。$80$分。
$T2$看了一眼,想到卡特兰数。
最后一直想推组合数,然后一直不对。。最后$QJ$了测试点拿到$10$分。
然后就跳过了。。
看了一眼$T3$,明显的$dfs$可拿到多半的分数,然后就跳过了。。。开始推$T2$的式子。(不知道当时怎么想的)
然后快$9:40$的时候才开始码$T3$,
最后码完这水的一批的样例直接过。。
其实中间都是错误。。最后不可避免的$WA 0$。
考完试改了一下然后拿到了正常分数$60$,
所以最后$80+10+0=90$。
没什么水平。。。


