bzoj3551
本题强制在线，bzoj3545不强制在线
转自SFN1036的题解
一开始yy出了一种用可持久化线段树来维护可持久化的root数组，然后其他的就像离线那样，只是每次合并线段树的时候不改变原来两棵树的儿子，而是新建节点。恩理论上好像是可以的，但是懒得写。
这题可以用一种叫Kruskal重构树的东西来搞，具体看PoPoQQQ大爷的题解。
大概就是说一开始新图中没有边，做小生成树的时候，每次加入一条新边(u,v,w)，就在新图中新建一个节点t，权值为w，然后把u和v所在的子树分别变为t的子树。
这样搞出来的新树有一些很棒的性质：
1、除了叶节点外，这是个大根堆。
2、一对点(u,v)在原树中路径上的边权最大值等于其在新树上的lca的权值。
这样的话，每次询问的时候我们就可以用倍增求出v的深度最小且权值不大于w的祖先a，那么显然a的子树内的点即是v能到达的所有点。
那么我们就可以用dfs序+可持久化线段树来搞了。
强制在线没法排序 启发式合并也就用不了了
Kruskal重构树是个挺好玩的东西 可以拿来处理一些最小生成树的边权最值问题
这里我们Kruskal连边时并不直接连边 而是新建一个节点ext 将两个点所在子树都连到ext的儿子上
比如说样例的树就建成了这样
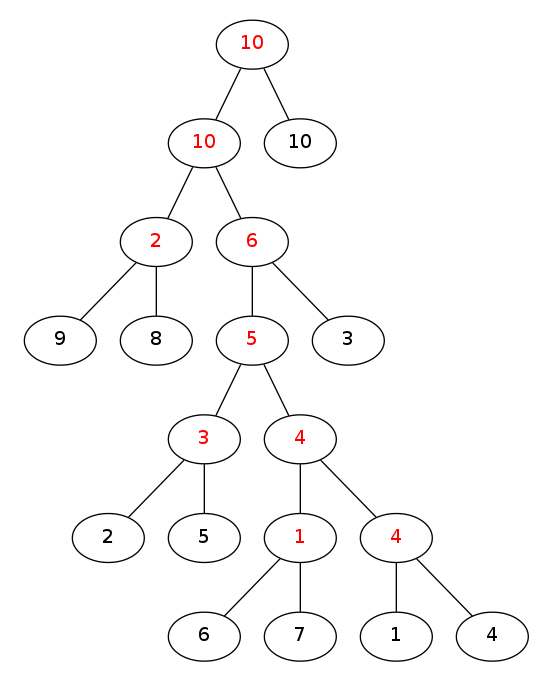
图中红色的是原图的边权，黑色的是原图上的点
这样生成的树有一些十分优美的性质：
1.二叉树(好吧这题意义不大)
2.原树与新树两点间路径上边权(点权)的最大值相等
3.子节点的边权小于等于父亲节点(大根堆)
4.原树中两点之间路径上边权的最大值等于新树上两点的LCA的点权
于是对于每个询问 我们从这个询问向上倍增寻找深度最小的点权小于等于x的点 易证这个节点的子树就是v所能到达的所有点
DFS序+可持久化线段树直接搞就行
#include<cstdio>
#include<cctype>
#include<algorithm>
inline void read(int &x){
char ch=getchar();x=0;
for(;!isdigit(ch);ch=getchar());
for(;isdigit(ch);ch=getchar())x=(x<<1)+(x<<3)+ch-'0';
}
const int N=1e5+5;
struct edge{int u,v,w;}e[N*5];
struct data{int l,r,s;}t[N<<5];
int siz,f[N<<1][20],dfn[N],mn[N<<1],mx[N<<1];
int tim,n,m,q,tot,val[N<<1],rt[N],a[N],fa[N<<1],head[N<<1],nex[N<<1],to[N<<1],cnt;
inline void addedge(int u,int v){
nex[++cnt]=head[u],head[u]=cnt,to[cnt]=v;
}
bool cmp(edge a,edge b){return a.w<b.w;}
inline int min(int a,int b){return a<b?a:b;}
inline int max(int a,int b){return a>b?a:b;}
inline int getfa(int x){return x==fa[x]?x:fa[x]=getfa(fa[x]);}
inline void dfs(int x){
if(x<=n)mn[x]=mx[x]=++tim,dfn[tim]=x;else mn[x]=n+1;
for(int i=1;i<20;i++)f[x][i]=f[f[x][i-1]][i-1];
for(int i=head[x];i;i=nex[i]){
f[to[i]][0]=x,dfs(to[i]),mn[x]=min(mn[x],mn[to[i]]),mx[x]=max(mx[x],mx[to[i]]);
}
}
inline void insert(int &p,int q,int l,int r,int x){
p=++siz,t[p]=t[q],t[p].s++;
if(l==r)return;int mid=l+r>>1;
if(x<=mid)insert(t[p].l,t[q].l,l,mid,x);else insert(t[p].r,t[q].r,mid+1,r,x);
}
inline int get(int x,int w){
for(int i=19;i>=0;i--)if(f[x][i]&&val[f[x][i]]<=w)x=f[x][i];
return x;
}
inline int query(int p,int q,int l,int r,int x){
if(t[p].s-t[q].s<x)return -1;
if(l==r)return l;
int mid=l+r>>1;
if(t[t[p].r].s-t[t[q].r].s>=x)return query(t[p].r,t[q].r,mid+1,r,x);
else return query(t[p].l,t[q].l,l,mid,x-t[t[p].r].s+t[t[q].r].s);
}
int main(){
read(n),read(m),read(q),tot=n;
for(int i=1;i<=n;i++)read(val[i]),a[i]=val[i];
std::sort(a+1,a+n+1);
int a1=std::unique(a+1,a+n+1)-a-1;
for(int i=1;i<=(n<<1);i++)fa[i]=i;
for(int i=1;i<=n;i++)val[i]=std::lower_bound(a+1,a+a1+1,val[i])-a;
for(int u,v,wi,i=1;i<=m;i++)read(e[i].u),read(e[i].v),read(e[i].w);
std::sort(e+1,e+m+1,cmp);
for(int i=1;i<=m;i++){
int fx=getfa(e[i].u),fy=getfa(e[i].v);
if(fx!=fy){
val[++tot]=e[i].w,addedge(tot,fx),addedge(tot,fy),fa[fx]=fa[fy]=tot;
}
}
dfs(tot);
for(int i=1;i<=n;i++)insert(rt[i],rt[i-1],1,n,val[dfn[i]]);
int ans=0;
while(q--){
int v,x,k;read(v),read(x),read(k);
int p=get(v,x);ans=query(rt[mx[p]],rt[mn[p]-1],1,n,k);
if(ans>-1)ans=a[ans];printf("%d\n",ans);
}
return 0;
}
