【数学】数学相关口胡
正经人谁学数论啊
持续更新。咕咕咕
右键数学公式\(\rightarrow\)Math Settings\(\rightarrow\)Math Renderer\(\rightarrow\)CommonHTML以获得更佳体验。
欢迎找锅
UPD on 9.17:补了补欧拉函数,中国剩余定理相关,加上了一些组合计数相关,修了修部分地方的排版
UPD on 9.18:添加了 Min-max 容斥内容。
UPD on 9.22:About exCRT。
UPD on 9.25:About exLucas。
小学生数论,并不适合dalao
质数
Eratosthenes筛素数
其实就是劣质版线性筛,不过代码比较短,打个小表还是可以的。
时间效率\(O(n\log \log n)\)
int Pri[maxn];
bool NotPri[maxn];
void JudPri(int n){
NotPri[0]=1;
NotPri[1]=1;//全局变量大括号赋值可是很不好的习惯哦...
for(int i=2;i<=n;i++){
if(NotPri[i])continue;
Pri[++Pri[0]]=i;
for(int j=i;(long long)i*j<=n;j++)
NotPri[i*j]=1;
}
}
线性筛素数
普通版
int Pri[maxn];
bool NotPri[maxn];
void JudPri(int n){
NotPri[0]=1;
NotPri[1]=1;
for(int i=2;i<=n;i++){
if(!NotPri[i]){
Pri[++Pri[0]]=i;
}
for(int j=1;j<=Pri[0]&&i*Pri[j]<=n;j++){
NotPri[i*Pri[j]]=1;
if(i%Pri[j]==0)break;
}
}
}
无需取模版
int v[maxn],Pri[maxn];
void JudPri(int n){
for(int i=2;i<=n;i++){
if(v[i]==0){
v[i]=i;
Pri[++Pri[0]]=i;
}
for(int j=1;j<=Pri[0];j++){
if(i*Pri[j]>n||Pri[j]>v[i])break;
v[i*Pri[j]]=Pri[j];
}
}
}
可能玄学上更快?(大雾)不过可能普通版的bool数组更快也说不定呢(好像真的会快很多)。
Miller_Rabin大素数判定
(所以名字到底事Robbin还是Rabin还是Rabbin?)
前置芝士:费马小定理
注:本文仅介绍简易版写法,深入学习建议看Gary_818的博客。
是看脸的随机化算法,错误率基本趋近于0。
0202年了不会还有人\(O(\sqrt n)\)判断素数吧不会吧不会吧
这种判断素数的方法利用的是的逆命题,随机枚举一个\(a\),满足这个同余式,那么\(p\)就是素数。
不过其逆命题并不是个真命题(大雾),例如在\(p=341\)的时候若\(a=2\)满足费马小定理,然而341是一个合数(\(341=11\times 31\))。因此仅判断一次得到的结果不一定正确,那怎么增大正确率呢?
那就是重复判断30次
时间复杂度\(O(\log\ n)\)(忽略常数)
#include<bits/stdc++.h>
using namespace std;
const int count=30;
int n;
inline int qpow(int a,int b,int Mod){
int ans=1,base=a;
while(b){
if(b&1)ans=ans*base%Mod;
base=base*base%Mod;
b>>=1;
}
return ans;
}
bool Miller_Rabin(int n){
if(n==2)
return true;
for(int i=1;i<=count;i++){
int a=rand()%(n-2)+2;
if(qpow(a,n,n)!=a)
return false;
}
return true;
}
int main(){
srand(time(0));
scanf("%d",&n);
if(Miller_Rabin(n))
printf("Probably a prime.");
else
printf("A composite.");
printf("\n");
return 0;
}
约数
GCD
辗转相除法求GCD
各位dalao已经倒着都能写了。
辗转相除法求最大公约数。或者为了防止爆栈可以改成循环。
inline int gcd(int x,int y){
if(y==0)return x;
else return(y,x%y);
}
二进制方法求GCD
如果想优化(可能大数据可以优化几百\(\mathrm{ms}\))
就变成魔法少女就可以用二进制优化(不过平时基本也无用)
- \(a\),\(b\)为偶数,则\(\gcd(a,b)=2\times \gcd(a/2,b/2)\)。
- \(a\)为奇数,\(b\)为偶数,则\(\gcd(a,b)=\gcd(a,b/2)\)。
- \(a\),\(b\)为奇数。假设\(a\geq b\),则\(\gcd(a,b)=\gcd((a-b)/2,b)\)。
- \(a\)为\(0\),则返回\(b\)。
可以用手写abs和min卡常
inline ll abs(ll x){
return x<0?-x:x;
}
inline ll min(ll a,ll b){
return a<b?a:b;
}
inline ll gcd(ll a,ll b){
if(a==0)return b;
if(b==0)return a;
if(!(a&1)&&!(b&1))return 2*gcd(a>>1,b>>1);
else if(!(a&1))return gcd(a>>1,b);
else if(!(b&1))return gcd(a,b>>1);
else return gcd(abs(a-b),min(a,b));
}
没有取模操作会快很多。
更相减损术求GCD
懒得写,建议BFS。
高精度运算的时候可以用(不过既然都是要用高精度的题了为何不弃了呢)
裴蜀定理
设\(a,b\)是全不为零的整数,则存在整数\(x,y\),使得\(ax+by=\gcd(a,b)\)。
算数基本定理的推论
算数基本定理(唯一分解定理)
任意大于1的正整数\(N\)都可分解为有限个素数的乘积。
\(N=p_1^{c_1}p_2^{c_2}p_3^{c_3}\cdots p_m^{c_m}\)
其中\(c_i\)都是正整数,\(p_i\)都是素数且满足\(p_1<p_2<p_3⋯<p_m\)。
求正约数个数
\(N\)的正约数个数为\(\prod\limits^m_{i=1}(c_i+1)\)
线性筛求约数个数
int pri[maxn],minn[maxn];
int d[maxn];
bool notpri[maxn];
inline void euler(){
d[1]=1;
for(int i=2;i<=n;i++){
if(!notpri[i]){
pri[++pri[0]]=i;
d[i]=2;
minn[i]=1;
}
for(int j=1;j<=pri[0]&&i*pri[j]<=n;j++){
notpri[i*pri[j]]=1;
if(i%pri[j]==0){
minn[i*pri[j]]=minn[i]+1;
d[i*pri[j]]=d[i]/(minn[i]+1)*(minn[i*pri[j]]+1);
break;
}
minn[i*pri[j]]=1;
d[i*pri[j]]=d[i]*2;
}
}
}
约数和定理
\(N\)的所有正约数之和为\(\prod\limits^m_{i=1}(\sum\limits^{c_i}_{j=0}(p_i)^j)\)
线性筛求约数和
\(f_i\)表示\(i\)的约数和,\(g_i\)表示\(i\)的最小质因子\(p+p^1+p^2+\dots +p^k\)
void pre(){
g[1]=f[1]=1;
for(int i=2;i<=n;i++){
if(!v[i])v[i]=1,p[++tot]=i,g[i]=i+1,f[i]=i+1;
for (int j=1;j<=tot&&i*p[j]<=n;j++){
v[i*p[j]]=1;
if(i%p[j]==0){
g[i*p[j]]=g[i]*p[j]+1;
f[i*p[j]]=f[i]/g[i]*g[i*p[j]];
break;
}else{
f[i*p[j]]=f[i]*f[p[j]];
g[i*p[j]]=1+p[j];
}
}
}
for(int i=1;i<=n;i++)
f[i]=(f[i-1]+f[i])%Mod;
}
求正约数集合
一个大于1的正整数\(N\)的正约数集合可写作
试除法
时间效率\(O(\sqrt n)\)。不会有人不会吧不会吧不会吧。
倍数法
倍数法以\(O(nlog\ n)\)的效率求出\(1-n\)所有数的正约数集合,比试除法的\(O(n\sqrt n)\)快很多。
vector<int> fac[maxn];
for(int i=1;i<=n;i++)
for(int j=1;i*j<=n;j++)
fac[i*j].push_back(i);
欧拉函数
\(1-N\)中与\(N\)互质的数的个数称为欧拉函数。
性质
见下线性筛求欧拉函数
分解质因数求单个欧拉函数
根据欧拉函数的定义,我们可以通过暴力分解质因数来求单个数的欧拉函数。
int euler(int n){
int ans=n,m=sqrt(n);
for (int i=2;i<=m;i++){
if (n%i==0){
ans=ans/i*(i-1);
while(n%i==0)n/=i;
}
}
if(n>1)ans=ans*n*(n-1);
return ans;
}
Eratosthenes筛求欧拉函数
妹想到吧又事它,时间效率\(O(n\log n)\),虽然效率不高但是很短(?)
int phi[maxn];
void euler(int n){
for(int i=2;i<=n;i++)
phi[i]=i;
for(int i=2;i<=n;i++)
if(phi[i]==i)
for(int j=i;j<=n;j+=i)
phi[j]=phi[j]/i*(i-1);
}
线性筛求欧拉函数
涉及到欧拉函数的性质。
\(p\)是质数,则:
\(\varphi(p)=p-1\)
显然
若 \(p|n\) 且 \(p^2|n\),则 \(\varphi(n)=\varphi(n/p)\times p\)。
由积性函数的定义和唯一分解定理,\(\varphi(n)=\prod \limits_{i=1}^m\varphi(p_i^{c_i})\),因此:
根据欧拉函数的计算式,上式的答案就是 \(p\)。
若 \(p|n\) 且 \(p^2\not|n\),则\(\varphi(n)=\varphi(n/p)\times (p-1)\)。
可知 \(p\) 和 \(n/p\) 互质,根据积性函数定义可得,即 \(\varphi(n)=\varphi(n/p)\times \varphi(p)\ (\varphi(p)=p-1)\)。
运用这三个性质,我们可以用筛积性函数的方法来线性求出 \(1-n\) 的欧拉函数。
int pri[maxn],phi[maxn];
bool notpri[maxn];
void euler(int n){
notpri[0]=1;notpri[1]=1;
for(int i=2;i<=n;i++){
if(!notpri[i]){
pri[++pri[0]]=i;
phi[i]=i-1;
}
for(int j=1;j<=pri[0]&&i*pri[j]<=n;j++){
notpri[i*pri[j]]=1;
if(i%pri[j]==0){
phi[i*pri[j]]=phi[i]*pri[j];
break;
}else phi[i*pri[j]]=phi[i]*(pri[j]-1);
}
}
}
扩展欧几里得
深入学习建议看YouXam的博客。
扩展欧几里德定理(Extended Euclidean algorithm, EX(恶心)GCD)。
用于求\(ax+by=\gcd(a,b)\)的一组整数解。
int exgcd(int a,int b,int &x,int &y) {
if (b==0){
x=1;
y=0;
return a;//a为最大公约数
}
int ret=exgcd(b,a%b,x,y);
int t=x;
x=y;
y=t-a/b*y;
return ret;
}
设\(\gcd(a,b)=d\),对于更一般的方程\(ax+by=c\),它有解当且仅当\(d|c\)。可以先求出\(ax+by=d\)的一组特解\(x_0,y_0\),使其同时乘上\(\frac{c}{d}\),就得到了\(ax+by=c\)的一组特解\(\frac{c}{d}x_0,\frac{c}{d}y_0\)。
即\(ax+by=c\)通解可以表示为:
非平凡因子
若\(x\)能整除\(n\)且\(1<x<n\),则\(x\)是\(n\)的非平凡因子。
即一个数除1和本身外的约数。
质数没有非平凡因子。
Pollard_Pho大数字质因数分解
请先了解Miller_Rabin大素数判定算法。
Pollard Rho是一个非常玄学的方式,用于在\(O(n^{1/4})\)的期望时间复杂度内计算合数n的某个非平凡因子。事实上算法导论给出的是\(O(\sqrt p)\),\(p\)是\(n\)的某个最小因子,满足\(p\)与\(n/p\)互质。但是这些都是期望,未必符合实际。但事实上Pollard Rho算法在实际环境中运行的相当不错。
Pollard_Rho算法的大致流程是:先判断当前数是否是素数(Miller_Rabin)了,如果是则直接返回。如果不是素数的话,试图找到当前数的一个因子(可以不是质因子)。然后递归对该因子和约去这个因子的另一个因子进行分解。
即找到一个数\(s\)使\(1<\gcd(s,x)<x\),此时\(X\)可以被分解为\(\gcd(s,x)\)和\(\frac{x}{\gcd(s,x)}\)两部分递归处理。
那么怎么找到当前数\(n\)的一个因子呢,没错又事看脸的随机化算法(大雾),感觉有一点“试”的感觉。
我们\(rand()\)一个\(1-x-1\)内的数字设为\(v_0\),此时使\(v_i=(v_{i-1}^2+t)\%x\)直至\(v_i=v_0\)(\(t\)自己设定,例如114514一般设定成1就可以,但尽量不要设置成0或2)。(这其实是一个剩余系)
由于它某项的值仅由前一项决定,且每一项可能的取值是有限的,因此该数列一定会在经历一定次数的迭代后陷入循环,形成一个类似希腊字母rho(\(\rho\))的形状,因此得名。
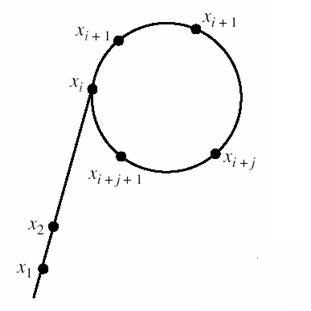
生日悖论:
23 个人里有两个生日相同的人的概率有多大呢?居然有 50%。不计特殊的年月,如 2 月 29 日。于是一年中有 N = 365 天。设房间里有 n 个人,要计算所有人的生日都不相同的概率。那么第一个人的生日是 365 选 365,第二个人是 365 选 364,第三个人 365 选 363 …… 第 n 个人的生日是 365 选 365-(n-1)。所以所有人生日都不相同的概率为\[\frac{365!}{365^n(365-n)!} \]可以看到n=100远小于N=365 时,就已经几乎必然有一对同生缘,所有人生日两两不同的概率仅一千万分之三。
N=365天中要出现两个生日相同的人,所需人数为\(n-O(\sqrt N)\)量级。
(懒得排版了,详细可以B(aidu)FS)
因此要求出现一对相同的数,其长度就大致为\(\sqrt n\)。
当\(v_i\equiv v_j\pmod p,v_i\not=v_j\)时,则\(p|(\vert v_i-v_j\vert )\)。计算\(\gcd(\vert v_i-v_j\vert ,p)\)即可达到一个\(x\)的非平凡因子\(p\)。
简易的实现方式:
设一个在环上的定点\(u\)和动点\(v\),经过多次迭代(约为\(x^{1/4}\))必定能找到\(u\equiv v\pmod p\)。
为了使\(u\)在环上,使其标号倍增。
ll Pollard_Rho(ll x){
ll v=rand(0,x-1);
ll u=v,d=1,i=0,temp=2;
while(d==1){
v=(v*v+1)%x;
d=gcd((ll)fabs(u-v),x);
i++;
if(i==temp){
u=v;//倍增
temp<<=1;
}
}
return d;
}
模板 Pollard-Rho算法
本题时间限制很紧,需要使用Floyed判环和倍增积累\(\gcd\)。而且数据范围很大,需要使用__int128(所以看看就好)
基于Floyed的实现:
使点\(u,v\)在同一起点出发,使\(u\)一倍速度迭代,\(v\)二倍速度迭代,当\(u\equiv v\pmod p\)就找到了环。这种方法比倍增方法快很多。
ll Pollard_Rho(ll x){
if(x==4)return 2;
ll u=rand(0,x-1),v=u;
ll d=1;
u=(u*u+1)%x;
v=(v*v+1)%x;v=(v*v+1)%x;
while(u!=v){
u=(u*u+1)%x;
v=(v*v+1)%x;v=(v*v+1)%x;
d=gcd((ll)fabs(u-v),x);
if(d!=1)return d;
}
return x;
}
倍增积累GCD:
每次的\(\vert u-v\vert\),若存在\(p|(\vert u_i-v_i\vert)\),则对于多个\(\vert u-v\vert\)的乘积\(Mul\),仍满足\(p|Mul\)。
因此我们可以先积累一定的答案再做\(\gcd\),毕竟\(\gcd\)不是\(O(1)\)的。
ll Pollard_Rho(ll x){
if(x==4)return 2;
ll u=rand(0,x-1),v=u;
ll d=1;
u=(u*u+1)%x;
v=(v*v+1)%x;v=(v*v+1)%x;
for(int i=1;u!=v;i=min(128,i<<1)){
ll Mul=1;
for(int j=0;j<i;j++){
ll temp=Mul*(ll)fabs(u-v)%x;
if(!temp)break;//abs(u-v)%x=0
Mul=temp;
u=(u*u+1)%x;
v=(v*v+1)%x;v=(v*v+1)%x;
}
d=gcd(Mul,x);
if(d!=1)return d;
}
return x;
}
本题代码:无
学习珂学
同余
费马小定理
不是小费马定理
前置芝士
剩余类&剩余系:总之大概就是一些数\(\mathrm{mod}\)一个正整数\(n\)之后都能得到什么结果(敷衍),最常用的完全剩余系\(\{0,1,…,n-1\}\)。
正文
若\(p\)为素数,且\(a\)不是\(p\)的倍数则:
另一个形式:若\(p\)为素数,对于任意整数\(a\):
证明:不会。建议记住(雾)。补上了
注:以下费马小定理、二次探测定理、威尔逊定理证明摘自博客。
考虑\(1,2,3...(p - 1)\)共\(p-1\)个数字,给所有数字同时乘\(a\),得到\(a,2a,3a,...(p - 1)a\)
欧拉定理
当模数为合数的时候需要用范围更广泛的欧拉定理。
若\(gcd(a,m)=1\),则:
扩展欧拉定理
证明
(好像没用过)
二次探测定理
若\(p\)为质数且\(x\in(0,p)\),则方程\(x^2 \equiv 1\pmod p\)的解为\(x = 1, x = p - 1\)。
证明:
Wilson定理
当且仅当\(p\)为素数时:\(( p -1 )! ≡ -1 \pmod p\)
乘法逆元
众所周知同余不满足同除性,所以数学家们弄出了逆元这个东西。
若整数\(b,m\)互质,且\(b|a\),则存在一个整数\(x\),使得\(a/b\equiv a\times x\pmod m\),则称\(x\)是\(b\)的模\(m\)的乘法逆元,记为\(b^{-1}\pmod m\)。
可见并不是所有数都存在逆元。
费马小定理求逆元
即\(a^{p-2}\pmod p\)。快速幂求解,很方便。
前提条件:模数为素数,且\(a\)不是\(p\)的倍数。有的题特意卡这个,例如沙拉公主的困惑。
欧拉定理求逆元
即\(a^{\varphi(p)-1}\pmod p\)
扩展欧几里得求逆元
求Exgcd(a, p)\(\rightarrow\)利用扩展欧几里得算法不断递归直到x=1,y=0\(\rightarrow\)反向递归求出第一层的x和y,x即为a模p的逆元。
前提条件:\(a\)和\(p\)互质。
#include<bits/stdc++.h>
using namespace std;
int b,x,y,mod;
inline int exgcd(int a,int b,int &x,int &y){
if(b==0){
x=1;
y=0;
return a;
}
int ret=exgcd(b,a%b,x,y);
int t=x;
x=y;
y=t-(a/b)*y;
return ret;
}
int main(){
scanf("%d%d",&b,&mod);
int gcd=exgcd(b,mod,x,y);
if(gcd!=1)
printf("None\n");
else
printf("%d\n",(x%mod+mod)%mod);
return 0;
}
线性求逆元
建议背式子
inv[1]=1;
for(int i=2;i<=n;i++)
inv[i]=(p-p/i)*inv[p%i]%p;
线性同余方程
(蒟蒻表示并不会高次的)
形如\(ax\equiv y\pmod b\)的方程被称为线性同余方程。
定理1:\(ax+by=c\iff ax\equiv c\pmod b\),有整数解的充要条件是\(\gcd(a,b)|c\)。
因此我们可以先用扩展欧几里得算法求出一组特解\(x_0,y_0\),则\(ax_0+by_0= \gcd(a,b)\)。此时两边同除\(\gcd(a,b)\),再同乘\(c\)。得到\(ac\cfrac{x_0}{\gcd(a,b)}+bc\cfrac{y_0}{\gcd(a,b)}=c\)。我们就得到了一个解\(\cfrac{x_0c}{\gcd(a,b)}\)。
定理2:若\(\gcd(a,b)=1\),且\(x_0,y_0\)为\(ax+by=c\)的一组解,则该方程的任意解可表示为\(x=x_0+bt,y=y_0-at\ (t\in \mathbb{Z})\)。
根据定理2求出的最小整数特解为:
方程的通解则是所有模\(\frac{b}{\gcd(a,b)}\)与\(x\)同余的整数。
int exgcd(int a,int b,int &x,int &y){
if(b==0){
x=1;
y=0;
return a;
}
int d=exgcd(b,a%b,x,y);
int t=x;
x=y;
y=t-a/b*y;
return d;
}
bool Cal(int a,int b,int c,int &x,int &y){
int d=exgcd(a,b,x,y);
if(c%d!=0)return 0;
int k=c/d;
x*=k;
y*=k;
return 1;
}
中国剩余定理
有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二。问物几何?
即求满足以下条件的整数:除以\(3\)余\(2\),除以\(5\)余 \(3\),除以\(7\)余\(2\)。
中国剩余定理(CRT)可求解如下形式的一元线性同余方程组(其中\(n_1,n_2,\dots,n_k\)两两互质)。
- 计算所有的模数的积\(n\);
- 对于第\(i\)个方程:
- 计算\(m_i=\frac{n}{n_i}\);
- 计算\(m_i\)在模\(n_i\)意义下的逆元\(m_i^{-1}\);在这里,需要使用 \(exgcd\) 计算逆元。
- 计算\(c_i=m_im_i^{-1}\)(不要对\(n_i\)取模)
- 方程的唯一解为:\(a=\sum\limits^k_{i=1}a_ic_i\pmod n\)
这里提供一个 \(exgcd+CRT\) 的板子。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e5+10;
int n,M=1,ans;
int a[maxn],b[maxn];
inline int read(){
int x=0;bool fopt=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')fopt=0;
for(;isdigit(ch);ch=getchar())x=(x<<3)+(x<<1)+ch-48;
return fopt?x:-x;
}
void exgcd(int a,int b,int &x,int &y){
if(!b)return x=1,y=0,void();
exgcd(b,a%b,x,y);
int z=x;x=y;y=z-(a/b)*y;
}
signed main(){
n=read();
for(int i=1;i<=n;i++){
a[i]=read();b[i]=read();
M*=a[i];
}
for(int i=1;i<=n;i++){
int m=M/a[i];
int x=0,y=0;
exgcd(m,a[i],x,y);
ans+=b[i]*m*(x<0?x+a[i]:x);
}
printf("%lld\n",ans%M);
return 0;
}
扩展中国剩余定理
若存在模数不互质的情况,则需要使用 \(exCRT\)。实际上就是解一元线性模线性方程组。
只考虑两个方程,多个方程可以两两合并。
设两个方程分别为 \(x\equiv a_1\pmod {m_1}\)、\(x\equiv a_2\pmod {m_2}\)
将其转为不定方程:\(x=m_1p+a_1=m_2q+a_2\ (p,q\in\mathbb{Z})\)
则有 \(m_1p-m_2q=a_2-a_1\)。
由裴蜀定理,\(\gcd(m_1,m_2)\not\vert \ (a_2-a_1)\) 时无解。
其他情况可通过扩展欧几里得得到一个 \(x'\) ,那么 \(p=x'\times \cfrac{a_2-a_1}{\gcd (m_2-m_1)}\pmod{m_2}\)。
则原两方程组成的模方程组的解为 \(x\equiv m_1p+a_1\pmod {\mathrm{lcm}(m_1,m_2)}\)
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e5+10;
int n;
int m[maxn],res[maxn];
inline int read(){
int x=0;bool fopt=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')fopt=0;
for(;isdigit(ch);ch=getchar())x=(x<<3)+(x<<1)+ch-48;
return fopt?x:-x;
}
inline int mul(int a,int b,int p){
int L=a*(b>>25LL)%p*(1LL<<25)%p;
int R=a*(b&((1LL<<25)-1))%p;
return (L+R)%p;
}
int exgcd(int a,int b,int &x,int &y){
if(!b)return x=1,y=0,a;
int gcd=exgcd(b,a%b,x,y);
int z=x;x=y;y=z-a/b*y;
return gcd;
}
inline int lcm(int a,int b,int gcd){
return a/gcd*b;
}
inline int exCRT(){
int M=m[1];
int ans=res[1]%m[1];
for(int i=2;i<=n;i++){
int x=0,y=0,temp=((res[i]-ans)%m[i]+m[i])%m[i];
int gcd=exgcd(M,m[i],x,y);
x=mul(x,temp/gcd,m[i]);
ans+=M*x;M=lcm(M,m[i],gcd);ans=(ans%M+M)%M;
}
return (ans%M+M)%M;
}
signed main(){
n=read();
for(int i=1;i<=n;i++){
m[i]=read();res[i]=read();
}
printf("%lld\n",exCRT());
return 0;
}
显然的是,\(exCRT\) 也能完美地解决普通 \(CRT\) 问题,而且长度差不多,所以如果只背一个板子的话建议背这个。
组合计数相关
Catalan数
以下问题属于 Catalan 数列:
1.有 \(2n\) 个人排成一行进入剧场。入场费 5 元。其中只有 \(n\) 个人有一张 5 元钞票,另外 \(n\) 人只有 10 元钞票,剧院无其它钞票,问有多少中方法使得只要有 10 元的人买票,售票处就有 5 元的钞票找零?
2.一位大城市的律师在她住所以北 \(n\) 个街区和以东 \(n\) 个街区处工作。每天她走 \(2n\) 个街区去上班。如果他从不穿越(但可以碰到)从家到办公室的对角线,那么有多少条可能的道路?(典型的 Cartalan 数问题)
3.在圆上选择 \(2n\) 个点,将这些点成对连接起来使得所得到的 \(n\) 条线段不相交的方法数?
4.对角线不相交的情况下,将一个凸多边形区域分成三角形区域的方法数?
5.一个栈(无穷大)的进栈序列为 \(1,2,3,\dots ,n\) 有多少个不同的出栈序列?
6.\(n\) 个结点可够造多少个不同的二叉树?
7.\(n\) 个不同的数依次进栈,求不同的出栈结果的种数?
8.生成字符串问题
Catalan 数的常见公式:
1.
Lucas定理
主要用于组合数取模。当数据较大的时候,直接求阶乘容易爆掉,这时候就需要用上 \(Lucas\) 定理了。
对于 \(C_{n/p}^{m/p}\),我们可以递归求解。
模板:
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e5+10;
int n,m,p;
int fac[maxn],inv[maxn];
inline int read(){
int x=0;bool fopt=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')fopt=0;
for(;isdigit(ch);ch=getchar())x=(x<<3)+(x<<1)+ch-48;
return fopt?x:-x;
}
inline int C(int N,int M){
if(M>N)return 0;
if(!M||N==M)return 1;
return fac[N]*inv[M]%p*inv[N-M]%p;
}
int Lucas(int N,int M,int P){
if(!M)return 1;
return C(N%P,M%P)*Lucas(N/P,M/P,P)%P;
}
signed main(){
int T=read();
while(T--){
n=read();m=read();p=read();
n+=m;
fac[0]=fac[1]=inv[0]=inv[1]=1;
for(int i=2;i<=p;i++)
inv[i]=(p-p/i)*inv[p%i]%p;
for(int i=2;i<=p;i++){
fac[i]=fac[i-1]*i%p;
inv[i]=inv[i-1]*inv[i]%p;
}
printf("%lld\n",(Lucas(n,m,p)+p)%p);
}
return 0;
}
扩展卢卡斯定理
篇幅过大,已搬出
容斥原理
Min-max容斥
篇幅过大,已搬出
概率与期望
莫比乌斯反演&&拉格朗日插值
建议问\(liuchanglc\)(滑稽)


