【考试反思】联赛模拟测试9

凯爹怒 \(\mathbb{AK}\) 钛聚辣
集训很长时间了,一直以为没有怎么挂分,结果今天直接打脸,再加上两道原题,人直接爆炸。
是状态的问题吗?不,就是菜吧。
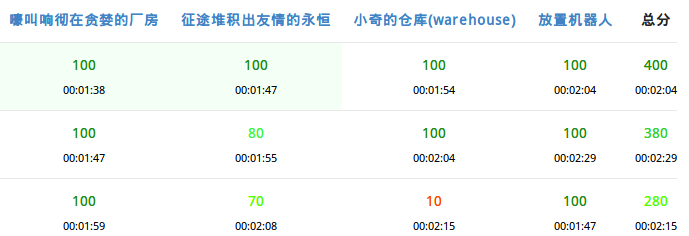
T1: 60 \(\rightarrow\) 20
T2: 60 \(\rightarrow\) 15
T3: 50 \(\rightarrow\) 30
T4: 100 \(\rightarrow\) 20
T1:嚎叫响彻在贪婪的厂房
考场上没想到用 set然后 \(O(n^2\log n)\) 暴力排序的,莫名其妙挂了。
根据题目名字的提示我们可以想到贪心。
可以想到不合法的情况就是 \(\gcd=1\) 或相等,其他直接和前面合并即可。利用 set 做到 \(O(n\log n)\)。
#include <bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
int n,ans;
int a[maxn];
set<int> s;
inline int read(){
int x=0;bool fopt=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')fopt=0;
for(;isdigit(ch);ch=getchar())x=(x<<3)+(x<<1)+ch-48;
return fopt?x:-x;
}
int gcd(int x,int y){
if(y==0)return x;
return gcd(y,x%y);
}
int main(){
#ifndef LOCAL
freopen("factory.in","r",stdin);
freopen("factory.out","w",stdout);
#endif
n=read();
for(int i=1;i<=n;i++)
a[i]=read();
int i=1;
while(i<=n){
if(i==n){
ans++;break;
}
int d=abs(a[i+1]-a[i]);
if(d==0||d==1){
ans++;i++;continue;
}
s.insert(a[i]);s.insert(a[i+1]);
int j;
for(j=i+2;j<=n;j++){
if(s.find(a[j])!=s.end())break;
d=gcd(d,abs(a[j]-*s.begin()));
if(d==1)break;
s.insert(a[j]);
}
i=j;ans++;s.clear();
}
printf("%d\n",ans);
return 0;
}
T2:征途堆积出友情的永恒
\(O(n^2)\) 的暴力很好写,但是人傻了,忘记可以从出发点直接开到现在,而且特判的分数也没写全。
memset(f,0x3f,sizeof(f));
f[0]=0;//删掉60->15,人傻了
f[1]=max(b[0],a[1]);
for(register int i=2;i<=n;i++)
for(register int j=i;j>=0&&i-j<=K;j--)
f[i]=min(f[i],f[j]+max(b[j],sum[i]-sum[j]));
ans=f[n];
简单的转移方程写出来之后,根据题目名字的提示我们想到了用堆优化转移。
对于 \(j\),\(f[j]+b[j]\) 和 \(f[j]-sum[j]\) 都是确定的。
那么就关于这两个东西维护两个小根堆。同时要注意因为在 \(b[j]>sum[i]-sum[j]\) 时第一个堆里的元素才会合法,所以首先把所有堆 1 里不合法的 pop,但要把它推入堆 2。
上面那个操作之前,之后,都要 pop 在距离上 \(>k\) 的点。如果之后不 pop ,会错一个点。
while循环很带感
#include <bits/stdc++.h>
using namespace std;
const int maxn=5e5+10;
int n,K;
long long ans;
int a[maxn],b[maxn];
long long sum[maxn],f[maxn];
struct Node{
int x;
long long w;
friend inline bool operator <(register const Node& A,register const Node& B){
return A.w>B.w;
}
};
inline int read(){
int x=0;bool fopt=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')fopt=0;
for(;isdigit(ch);ch=getchar())x=(x<<3)+(x<<1)+ch-48;
return fopt?x:-x;
}
priority_queue<Node> q1,q2;
int main(){
#ifndef LOCAL
freopen("empire.in","r",stdin);
freopen("empire.out","w",stdout);
#endif
n=read();K=read();
for(int i=1;i<=n;i++){
a[i]=read();
sum[i]=sum[i-1]+a[i];
}
for(int i=1;i<=n;i++)
b[i-1]=read();
memset(f,0x3f,sizeof(f));
f[0]=0;
for(int i=1;i<=n;i++){
q1.push((Node){i-1,f[i-1]+b[i-1]});
while(!q1.empty()){
Node x=q1.top();
if(x.x>=i-K)break;
q1.pop();
}
while(!q2.empty()){
Node x=q2.top();
if(x.x>=i-K)break;
q2.pop();
}
while(!q1.empty()){
Node x=q1.top();
if(x.w>f[x.x]+sum[i]-sum[x.x])break;
q1.pop();q2.push((Node){x.x,f[x.x]-sum[x.x]});
}
while(!q1.empty()){
Node x=q1.top();
if(x.x>=i-K)break;
q1.pop();
}
while(!q2.empty()){
Node x=q2.top();
if(x.x>=i-K)break;
q2.pop();
}
long long temp=0x3f3f3f3f3f3f3f3f;
if(!q1.empty())temp=min(temp,q1.top().w);
if(!q2.empty())temp=min(temp,q2.top().w+sum[i]);
f[i]=temp;
}
printf("%lld\n",f[n]);
return 0;
}
T3:小奇的仓库
这个人更傻了,之前还写过题解的。
基础的换根 \(DP\) 的分怎么没拿到呢?快和小编来看一看吧。
void dfs2(int u,int fa){
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==fa)continue;
f[v]=f[u]+(n-siz[v])*e[i].w-siz[v]*e[i].w;
dfs2(v,u);//考场没写这句
}
}
由于样例只有一层,所以我并没有看出来我写挂了:D。
注意其算的是异或后的差值,所以最后统一修改是正确的。可以手模一下。
T4:放置机器人
二分图练习里就这道题没写:D。人都傻掉了。
考场上拆行拆列都写了,结果没想到最后打败我的是匈牙利的板子忘掉了。事实上,还是对匈牙利的本质没有弄清。
bool vis[maxn];
int match[maxn];
bool dfs(int u){
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(vis[v])continue;
vis[v]=1;
if(!match[v]||dfs(match[v])){//考场写的dfs(v)
match[v]=u;return 1;
}
}
return 0;
}
考虑墙对答案的影响,无非就是墙将本来属于一行的拆成了多行,将本来属于一列的拆成了多列。所以我们将行和列重新标号之后,就变成了裸的二分图放置问题。
#include <bits/stdc++.h>
using namespace std;
const int maxn=3000+10;
int n,m,ans;
char s[60][60];
struct Edge{
int from,to,nxt;
}e[maxn<<1];
int head[maxn],cnt;
inline void add(int u,int v){
e[++cnt].from=u;
e[cnt].to=v;
e[cnt].nxt=head[u];
head[u]=cnt;
}
inline int Get(int x,int y){
return m*(x-1)+y;
}
int belrow[maxn],belcol[maxn];
bool vis[maxn];
int match[maxn];
bool dfs(int u){
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(vis[v])continue;
vis[v]=1;
if(!match[v]||dfs(match[v])){
match[v]=u;return 1;
}
}
return 0;
}
int main(){
#ifndef LOCAL
freopen("robots.in","r",stdin);
freopen("robots.out","w",stdout);
#endif
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%s",s[i]+1);
for(int i=1;i<=n;i++){
belrow[0]++;
for(int j=1;j<=m;j++){
if(s[i][j]=='o'){
belrow[Get(i,j)]=belrow[0];
}else if(s[i][j]=='#'&&j!=m&&s[i][j+1]!='#')belrow[0]++;
}
}
for(int j=1;j<=m;j++){
belcol[0]++;
for(int i=1;i<=n;i++){
if(s[i][j]=='o'){
belcol[Get(i,j)]=belcol[0];
}else if(s[i][j]=='#'&&i!=n&&s[i+1][j]!='#')belcol[0]++;
}
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(s[i][j]=='o')add(belrow[Get(i,j)],belcol[Get(i,j)]);
for(int i=1;i<=belrow[0];i++){
memset(vis,0,sizeof(vis));
if(dfs(i))ans++;
}
printf("%d\n",ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号