利用奇异值分解(SVD)进行图像压缩-python实现

首先要声明，图片的算法有很多，如JPEG算法，SVD对图片的压缩可能并不是最佳选择，这里主要说明SVD可以降维

相对于PAC（主成分分析），SVD（奇异值分解）对数据的列和行都进行了降维，左奇异矩阵可以用于行数的压缩。相对的，右奇异矩阵可以用于列数即特征维度的压缩，也就是我们的PCA降维。

一张二维n*m的灰度图片可以看做是n*m的矩阵，利用SVD可以实现对二维图像的压缩

1、按照灰度图片进行压缩：

#-*- coding: utf-8 -*
import numpy as np
from PIL import Image

def svd_restore(sigma, u, v, K):
    K = min(len(sigma)-1, K)            #当K超过sigma的长度时会造成越界
    print 'Now restore the image with %d ranks' % K
    m = len(u)
    n = v[0].size
    SigRecon = np.zeros((m, n))         #新建一int矩阵，储存恢复的灰度图像素
    for k in range(K+1):                #计算X=u*sigma*v
        for i in range(m):
            SigRecon[i] += sigma[k] * u[i][k] * v[k]
    SigRecon = SigRecon.astype('uint8') #计算得到的矩阵还是float型，需要将其转化为uint8以转为图片
    Image.fromarray(SigRecon).save("svd_" + str(K) + "_" +image_file) #保存灰度图
    
image_file = u'1.jpg'
if __name__ == '__main__':
    im = Image.open(image_file)    #打开图像文件
    im = im.convert('L')           #将原图像转化为灰度图
    im.save("Gray_" + image_file)  #保存灰度图
    w, h = im.size                 #得到原图的长与宽
    dt = np.zeros((w, h), 'uint8') #新建一int矩阵，储存灰度图各像素点数据
    for i in range(w):             #逐像素点复制，由于直接对im.getdata()进行数据类型转换会有偏差
        for j in range(h):
            dt[i][j] = im.getpixel((i, j))
    dt = dt.transpose()            #复制过来的图像是原图的翻转，因此将其再次翻转到正常角度
    u, sigma, v = np.linalg.svd(dt)#调用numpy库进行SVM
    u = np.array(u)                #转为array格式，方便进行乘法运算
    v = np.array(v)                #同上
    for k in [1, 10, 20, 30, 50, 80, 100, 150, 200, 300, 500]:
        svd_restore(sigma, u, v, k)#使用前k个奇异值进行恢复

奇异值分别取1, 10, 20, 30, 50, 80, 100, 150, 200, 300, 500的降维压缩效果（原始图片为1.jpg）

2、按照彩色图片进行压缩

#-*- coding: utf-8 -*
from PIL import Image 
import numpy as np 
def rebuild_img(u, sigma, v, p):#p表示奇异值的百分比 
    #print p 
    m = len(u) 
    n = len(v) 
    a = np.zeros((m, n)) 

    count = (int)(sum(sigma)) 
    curSum = 0 
    k = 0 
    print sigma[0:2],count* p
    while curSum <= count * p:
        uk = u[:, k].reshape(m, 1)
        vk = v[k].reshape(1, n) 
        #print curSum,count,'--------',k
        a += sigma[k] * np.dot(uk, vk)
        curSum += sigma[k] 
        k += 1
        #print k
    
    print 'k:',k 
    a[a < 0] = 0 
    a[a > 255] = 255
     #按照最近距离取整数，并设置参数类型为uint8 
    return np.rint(a).astype("uint8") 
if __name__ == '__main__':
    img = Image.open(u'招商.jpg', 'r')
    a = np.array(img)
    #print a[:, :, 0]
    # u, sigma, v = np.linalg.svd(a[:, :, 0])
    # R = rebuild_img(u, sigma, v, 0.9)

    for p in np.arange(0.1, 1, 0.1):
        u, sigma, v = np.linalg.svd(a[:, :, 0])
        R = rebuild_img(u, sigma, v, p)
        u, sigma, v = np.linalg.svd(a[:, :, 1])
        G = rebuild_img(u, sigma, v, p)
        u, sigma, v = np.linalg.svd(a[:, :, 2])
        B = rebuild_img(u, sigma, v, p)
        I = np.stack((R, G, B), 2)
        #保存图片在img文件夹下
        Image.fromarray(I).save("aq\\svd_" + str(int(p * 100)) + ".jpg")

RGB三个通道信息量均按照按照0.1-0.9压缩的图片对比：

2、matplotlib展示压缩前后对比（灰度）

 

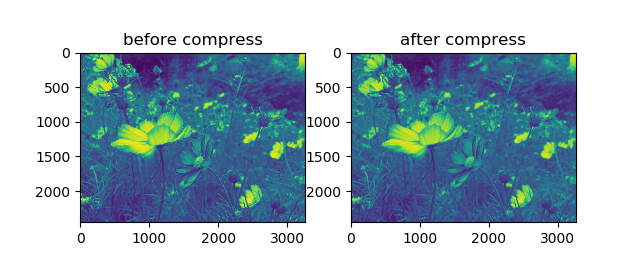
#-*- coding: utf-8 -*
import numpy as np
from scipy import ndimage
import matplotlib.pyplot as plt
def pic_compress(k, pic_array):
    u, sigma, vt = np.linalg.svd(pic_array)
    sig = np.eye(k) * sigma[: k]
    new_pic = np.dot(np.dot(u[:, :k], sig), vt[:k, :])  # 还原图像
    size = u.shape[0] * k + sig.shape[0] * sig.shape[1] + k * vt.shape[1]  # 压缩后大小
    return new_pic, size

filename = u"招商.jpg" 
ori_img = np.array(ndimage.imread(filename, flatten=True)) 
new_img, size = pic_compress(100, ori_img) 
print("original size:" + str(ori_img.shape[0] * ori_img.shape[1])) 
print("compress size:" + str(size)) 
fig, ax = plt.subplots(1, 2) 
ax[0].imshow(ori_img) 
ax[0].set_title("before compress") 
ax[1].imshow(new_img) 
ax[1].set_title("after compress") 
plt.show()

 

运行效果：

 

参考文献：

https://my.oschina.net/bgbfbsdchenzheng/blog/687110

https://blog.csdn.net/xuelabizp/article/details/52318708

https://blog.csdn.net/wang454592297/article/details/80999644