20162309《程序设计与设计结构》第四次实验报告
实验名称:图的实现和应用
实验目的:学习图的相关内容,掌握图的构建方法,实现图结构,初步了解十字链表和邻接矩阵的使用方法,以及对图结构实现过程的应用。掌握图结构对最短路径的求值方法,学习带权图。
实验题目:1.用邻接矩阵实现无向图(边和顶点都要保存),实现在包含添加和删除结点的方法,添加和删除边的方法,size(),isEmpty(),广度优先迭代器,深度优先迭代器,给出伪代码,产品代码,测试代码(不少于5条测试)
2.用十字链表实现无向图(边和顶点都要保存),实现在包含添加和删除结点的方法,添加和删除边的方法,size(),isEmpty(),广度优先迭代器,深度优先迭代器,给出伪代码,产品代码,测试代码(不少于5条测试)
3.实现PP19.9,给出伪代码,产品代码,测试代码(不少于5条测试)
实验具体过程:
实验1.用邻接矩阵实现无向图。首先需要了解邻接矩阵的相关内容:
邻接矩阵(Adjacency Matrix):是表示顶点之间相邻关系的矩阵。设G=(V,E)是一个图,其中V={v1,v2,…,vn}。在无向图的结构中,邻接矩阵的n阶方阵性质如下:
①对无向图而言,邻接矩阵一定是对称的,而且主对角线一定为零(在此仅讨论无向简单图),副对角线不一定为0,有向图则不一定如此。
②在无向图中,任一顶点i的度为第i列(或第i行)所有非零元素的个数,在有向图中顶点i的出度为第i行所有非零元素的个数,而入度为第i列所有非零元素的个数。
③用邻接矩阵法表示图共需要n^2个空间,由于无向图的邻接矩阵一定具有对称关系,所以扣除对角线为零外,仅需要存储上三角形或下三角形的数据即可,因此仅需要n(n-1)/2个空间。
对于实验一需要实现的无向图,在无向图的邻接矩阵中存在以下特点:
1.无向图的邻接矩阵一定是对称的,而有向图的邻接矩阵不一定对称。因此,用邻接矩阵来表示一个具有n个顶点的有向图时需要n^2个单元来存储邻接矩阵;对有n个顶点的无向图则只存入上(下)三角阵中剔除了左上右下对角线上的0元素后剩余的元素,故只需1+2+...+(n-1)=n(n-1)/2个单元。
2.无向图邻接矩阵的第i行(或第i列)非零元素的个数正好是第i个顶点的度。
3.有向图邻接矩阵中第i行非零元素的个数为第i个顶点的出度,第i列非零元素的个数为第i个顶点的入度,第i个顶点的度为第i行与第i列非零元素个数之和。
4.用邻接矩阵表示图,很容易确定图中任意两个顶点是否有边相连。
使用邻接矩阵实现图:因为图可以同时使用邻接矩阵和邻接表来实现,当由邻接矩阵来实现时,可以举这个例子:如下的无向图
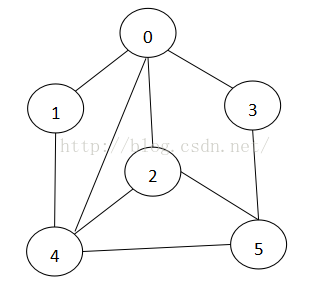
邻接矩阵是表示图形中顶点之间相邻关系的矩阵,对于n个顶点的图而言,矩阵是的row和col表示的是1....n个点。而且对于无向图如果顶点b1和b2是连接的,那么在二维矩阵中matrix[b1,b2]和matrix[b2,b1]位置的值置为1,如果是有向图b1指向b2,那么 matrix[b1,b2]=1,matrix[b2,b1]=0。此无向图使用邻接矩阵表示出来,用0/1表示结果如下:

如果图是一个带权图,需要把1换为相应边上的权值,把非对角线上的换成一个很大的特定的实数则可。
那么如何用java代码来实现图的邻接矩阵?首先结点的储存数据为char类,输入结点vexs以及边weight,这样就先创建了该邻接矩阵的数据储存结构:
public class MGraph {
int vexs; //图中结点数目
char data[]; //存放结点数据
int [][]weight; //存放边
public MGraph(int ve){
vexs=ve;
data=new char[ve];
weight=new int[ve][ve];
}
}
实现了储存结构后,需要的是创建图的邻接矩阵,也就是本个实验的核心部分,定义两个关键的值vexs和weight,则可以int一个i和j作为变量,然后定义边和结点之间的关系,就可以创建邻接矩阵了。
public void CreateGraph(MGraph graph,int vexs,char data[],int [][]weight){
int i,j;
for(i=0;i<vexs;i++){
graph.data[i]=data[i];
for(j=0;j<vexs;j++){
graph.weight[i][j]=weight[i][j];
}
}
}
创建后就需要考虑结点和顶点的问题,如何获得当前顶点和其第一个邻接定点的位置,同样需要定义变量来实现,这里则需要考虑当顶点的值超出范围时的情况,返回值则需要return -1;其次,扩展到第n个顶点,同样可以用类似的方法来处理。
public int GetFirst(MGraph graph,int k){
int i;
if(k<0||k>graph.vexs-1){
System.out.println("参数k值超出范围");
return -1;
}
for(i=0;i<graph.vexs;i++){
if(graph.weight[k][i]==1)
return i;
}
return -1;
} //第一个
public int GetNext(MGraph graph,int k,int n){
int i;
if(k<0||k>graph.vexs-1||n<0||n>graph.vexs-1){
System.out.println("参数k或t值超出范围");
return -1;
}
for(i=n+1;i<graph.vexs;i++){
if(graph.weight[k][i]==1)
return i;
}
return -1;
} //第n个
实现了邻接矩阵和顶点,接下来需要实现的是递归方式,根据要求可以将邻接矩阵分为优先深度遍历。可以设一个k为起始顶点,开始访问时定义visit来标记已经访问过的点,之后进行循环,不断获取下一个顶点,直到访问完成。这里需要额外注意一点,如果其中一个顶点没有被访问到的问题,在运行时则会自动递归访问该顶点的邻接点。
具体到代码的实现过程:
public void DFSVGraph(MGraph graph,int k,int visited[]){
int u; // 设立顶点k的邻接点
System.out.print(graph.data[k]+", ");
visited[k]=1;//表示顶点k被访问过
u=GetFirst(graph,k);//获取k的第一个邻接顶点u
while(u!=-1){
if(visited[u]==0){ //如果u未被访问过,则递归访问u的邻接点
DFSVGraph(graph,u,visited);
}
u=GetNext(graph,k,u);//获取k的下一个邻接顶点
}
}
关于广度优先的遍历,可以使用于深度优先相似的操作步骤,在广度优先的实现中,可以使用有关队列的部分知识,将顶点作为入队和出队的元素来实现。同样设顶点,使用visit来标记已经被访问过的顶点。可以用remove来取出队列顶部的元素,使用isEmpty来判断队列元素,之后再进行循环操作。其他的方法,包括
具体代码实现:
public void BFSVGraph(MGraph graph,int k,int visited[]){
Queue <Integer>queue=new LinkedList <Integer>();
int u;
queue.add(k);//顶点k进入队列
visited[k]=1;//顶点k标记被访问过
while(!queue.isEmpty()){
u=queue.remove();//取出队列顶元素
System.out.print(graph.data[u]+", ");
int v=GetFirst(graph,u);//获取u的第一个邻接顶点v
while(v!=-1){
if(visited[v]==0){ //如果v未被访问过,则递归访问v的邻接点
queue.add(v);
visited[v]=1;//顶点v标记被访问过
}
v=GetNext(graph,u,v);//获取u的下一个邻接顶点
}
}
}
同样,当其中一个顶点没有被访问到时,会以递归访问来访问当前结点的邻接点。
邻接矩阵在无向图中的应用,可以通过以上方法来实现,在编写完测试类后可以得到运行结果:

在实现了邻接矩阵后,如何实现结点删除后,剩余结点和边的计算?这里可以先使用size方法来定义输入结点的个数,以及获得边的长度。首先需要的是初始化矩阵,令其为空。具体实现方法如下:
public AMWGraph(int n) {
//初始化矩阵,一维数组,和边的数目
edges=new int[n][n];
vertexList=new ArrayList(n);
numOfEdges=0;
}
定义新的结点和边的值,使其为空,也就是初始化。之后再输入结点和边:
//得到结点的个数
public int getNumOfVertex() {
return vertexList.size();
}
//得到边的数目
public int getNumOfEdges() {
return numOfEdges;
}
实现了这两个方法后,测试类的编写就可以加入结点删除了:
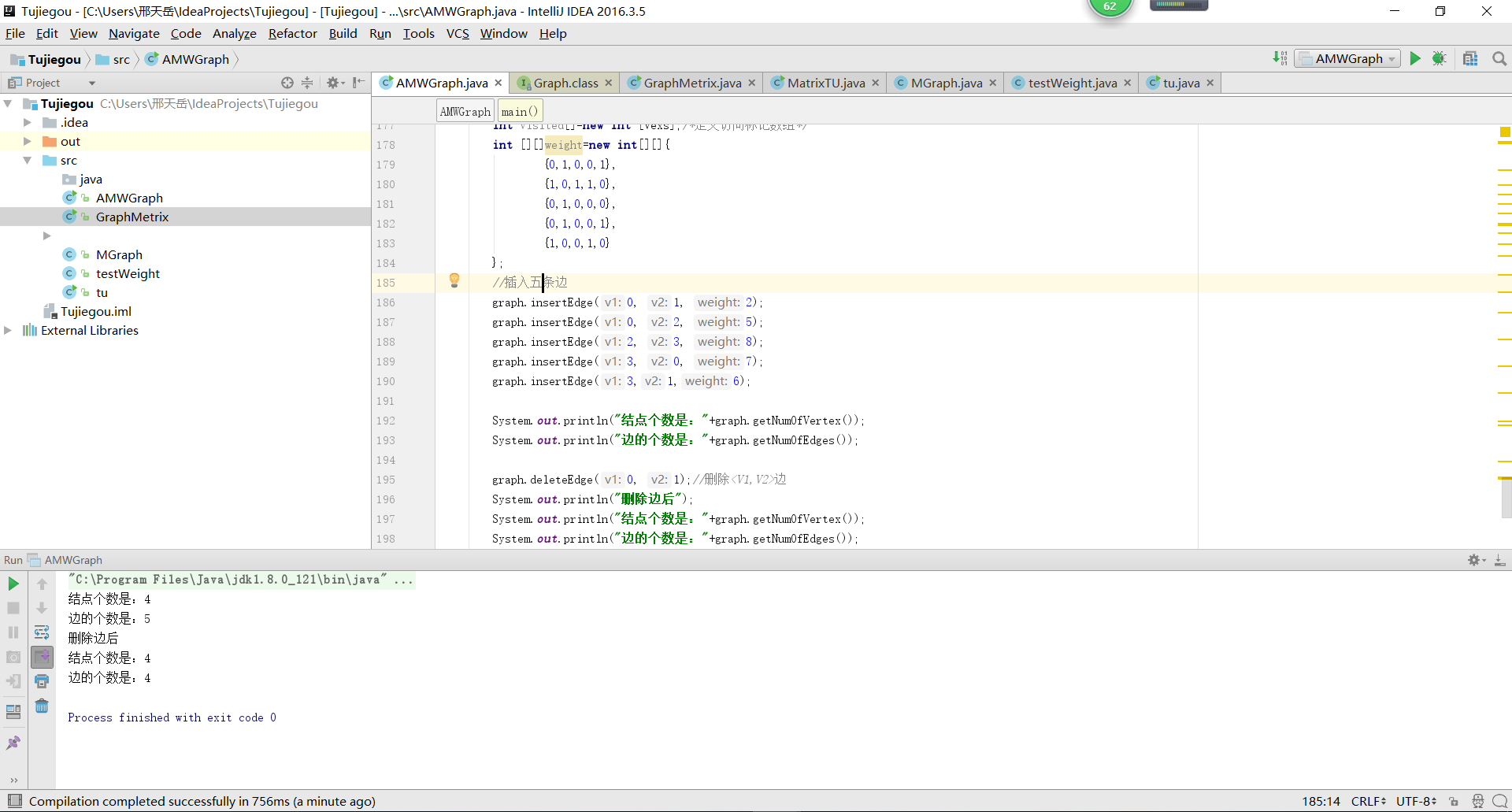
public static void main(String args[]) {
int n=4,e=4;
String labels[]={"V1","V1","V3","V4"};
AMWGraph graph=new AMWGraph(n);
for(String label:labels) {
graph.insertVertex(label);//插入结点
}
再输入五条边:
//插入五条边
graph.insertEdge(0, 1, 2);
graph.insertEdge(0, 2, 5);
graph.insertEdge(2, 3, 8);
graph.insertEdge(3, 0, 7);
graph.insertEdge(3, 1, 6);
边的添加和删除:
//插入边
public void insertEdge(int v1,int v2,int weight) {
edges[v1][v2]=weight;
numOfEdges++;
}
//删除边
public void deleteEdge(int v1,int v2) {
edges[v1][v2]=0;
numOfEdges--;
}
最后得到运行结果,可以比对结点删除前后边的变化:
邻接矩阵的使用过程可以由以上方法实现,第二个需要实现的是十字链表来实现无向图。
2.十字链表
可以看作是将有向图的邻接表和逆邻接表结合起来得到的。用十字链表来存储有向图,可以达到高效的存取效果。同时,代码的可读性也会得到提升。
实验同样需要构造函数,定义顶点和边,同样需要新定义char类,和实验一类似:
public OListDG(char[] vexs, char[][] edges) {
vlen = vexs.length;
elen = edges.length;
将顶点和边分开进行初始化,同时需要建立顶点表和十字链表,其中十字链表可以使用头插法建立。关于头插法和尾插法的相关内容介绍可由下图得到相对直观的解释:

具体的代码实现:
建立顶点表
// 初始化顶点,建立顶点表
vertexNodeList = new VertexNode[vlen];
for (int i = 0; i < vlen; i++) {
vertexNodeList[i] = new VertexNode();
vertexNodeList[i].vertex = vexs[i];
vertexNodeList[i].firstIn = null;
vertexNodeList[i].firstOut = null;
建立十字链表
// 初始化边,利用头插法建立十字链表
for (int i = 0; i < elen; i++) {
EdgeNode edgeNode_1 = new EdgeNode();
EdgeNode edgeNode_2 = new EdgeNode();
int vi = getPosition(edges[i][0], vexs);
int vj = getPosition(edges[i][1], vexs);
edgeNode_1.tailvex = vi;
edgeNode_1.headvex = vj;
edgeNode_1.taillink = vertexNodeList[vi].firstOut;
vertexNodeList[vi].firstOut = edgeNode_1;
edgeNode_2.tailvex = vi;
edgeNode_2.headvex = vj;
edgeNode_2.headlink = vertexNodeList[vj].firstIn;
vertexNodeList[vj].firstIn = edgeNode_2;
}
}
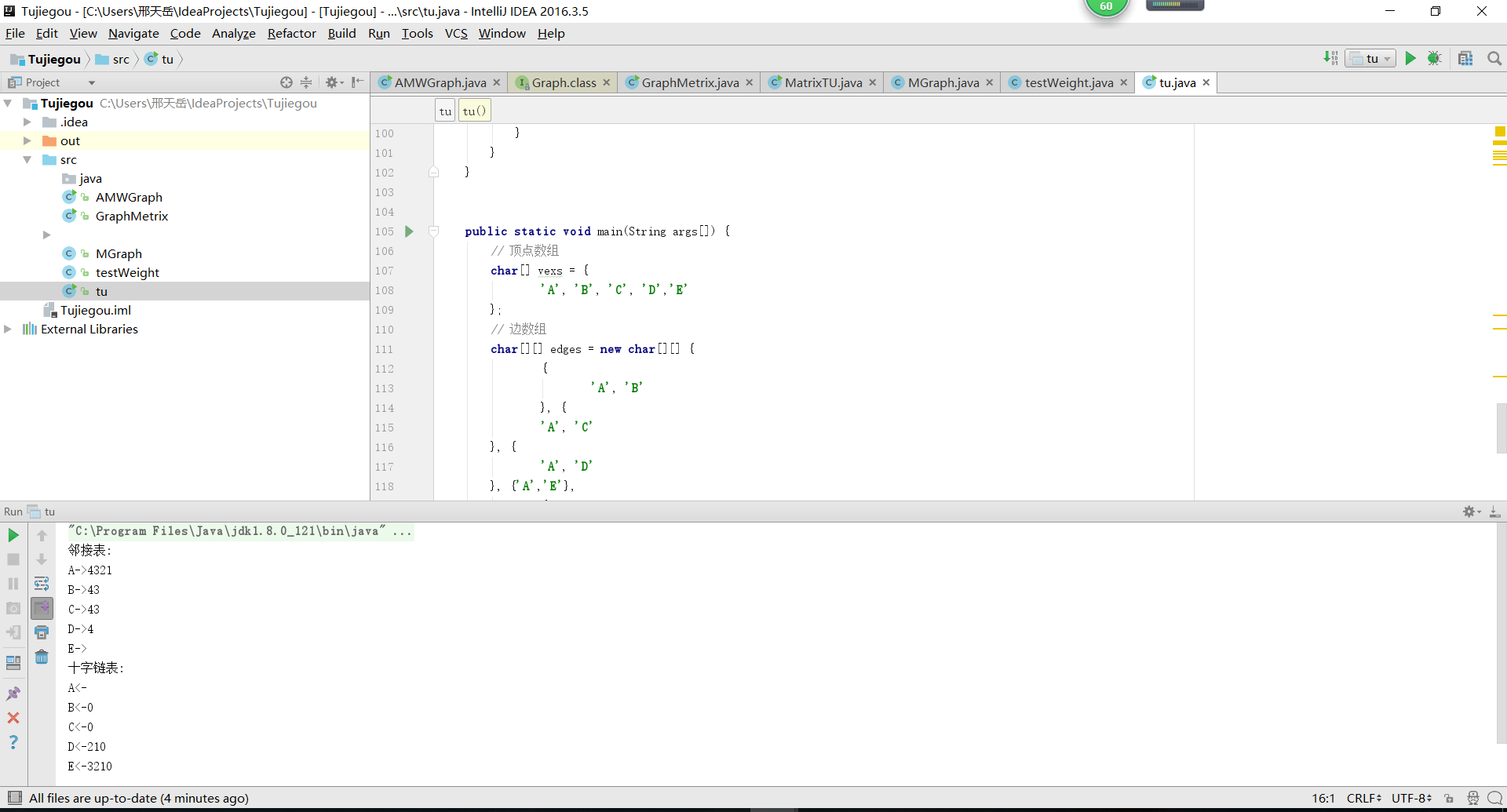
测试过程中需要先定义顶点组数,之后定义边的组数,最后获得结果:
3.求带权图的最短路径问题:
首先可以使用课上学习到Dijkstra方法:
Dijkstra算法是典型的算法。Dijkstra算法是很有代表性的算法。Dijkstra一般的表述通常有两种方式,一种用永久和临时标号方式,一种是用OPEN, CLOSE表的方式,这里均采用永久和临时标号的方式。注意该算法要求图中不存在负权边。
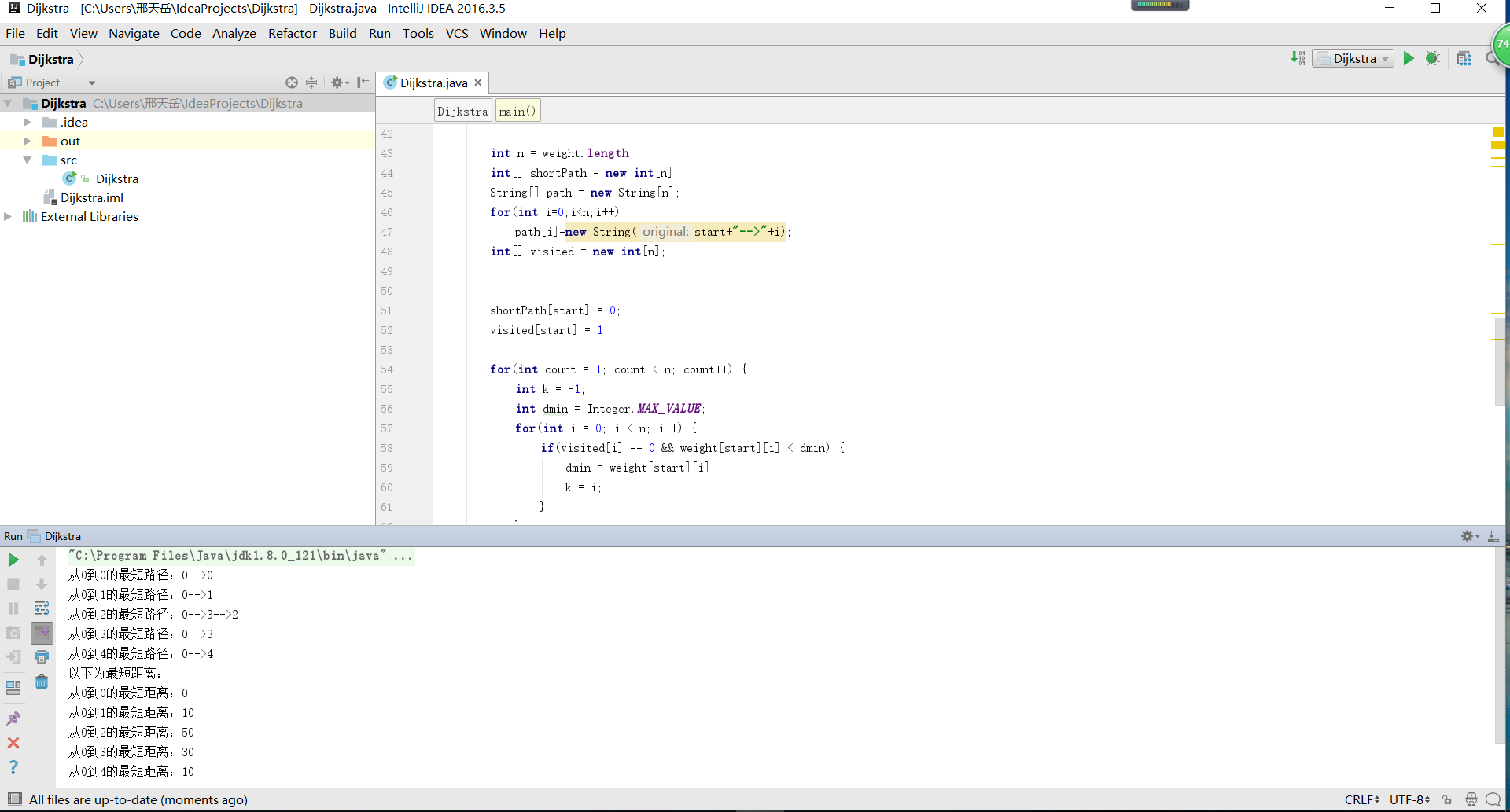
使用Dijkstra算法可以求得最短路径,具体实现过程如下:
获得路径:
public Node init(){
//初始路径,因没有A->E这条路径,所以path(E)设置为Integer.MAX_VALUE
path.put("B", 1);
pathInfo.put("B", "A->B");
path.put("C", 1);
pathInfo.put("C", "A->C");
path.put("D", 4);
pathInfo.put("D", "A->D");
path.put("E", Integer.MAX_VALUE);
pathInfo.put("E", "A");
path.put("F", 2);
pathInfo.put("F", "A->F");
path.put("G", 5);
pathInfo.put("G", "A->G");
path.put("H", Integer.MAX_VALUE);
pathInfo.put("H", "A");
//将初始节点放入close,其他节点放入open
Node start=new MapBuilder().build(open,close);
return start;
}
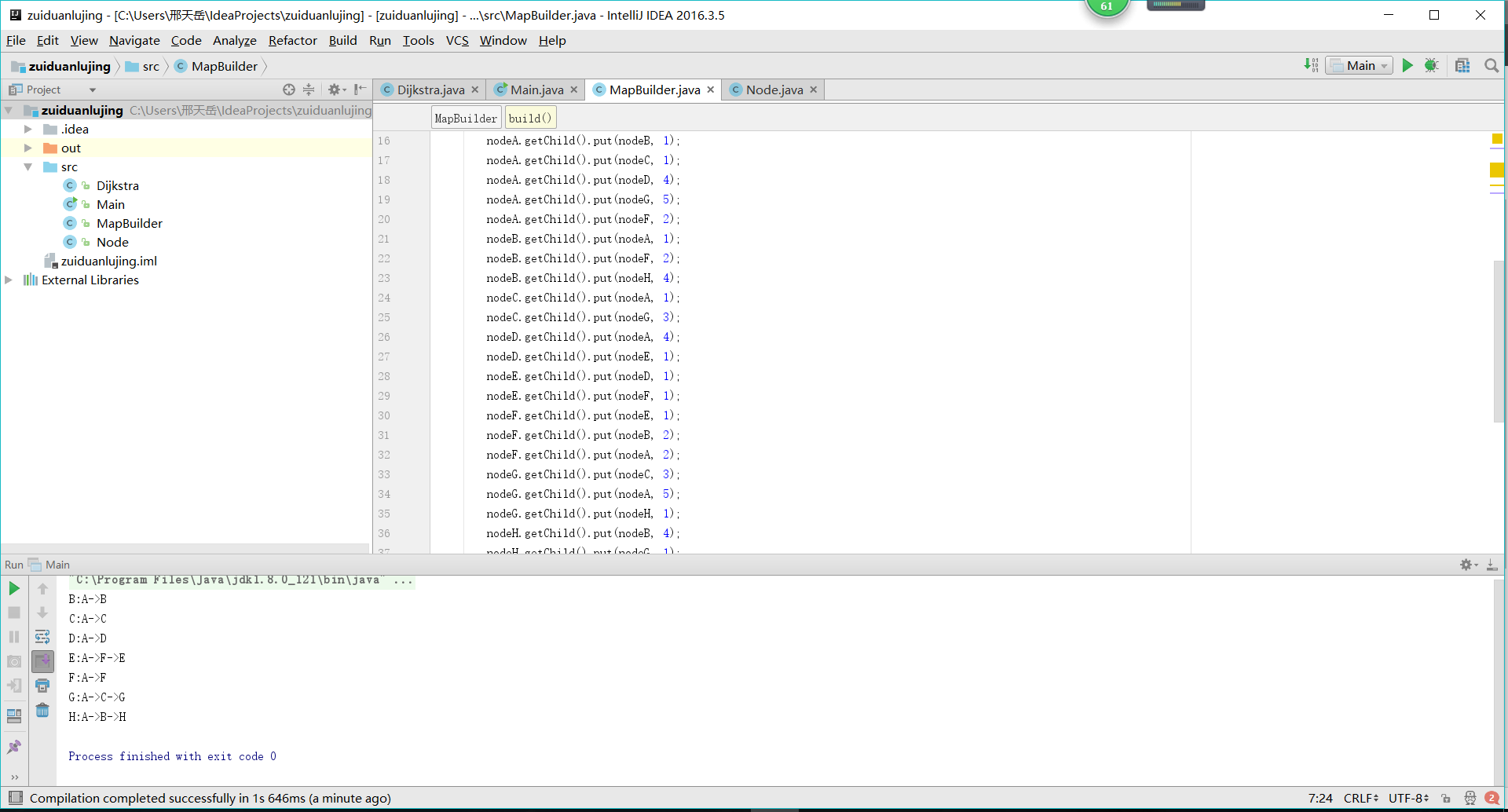
最后得到结果,给出路径:




 浙公网安备 33010602011771号
浙公网安备 33010602011771号