top cluster 树分块学习笔记

参考资料：周欣《浅谈一类树分块的构建算法及其应用》、@negiizhao Top tree 相关东西的理论、用法和实现、lxl [Ynoi2018] Day2 题解、@zhylj 「学习笔记」基于 Top Cluster 分解的树分块算法。

基本概念

一个树簇（cluster）是树上的一个连通点集，有至多两个点与外界连接。这两个点称为界点（boundary node），簇中其余的点称为内点（internal node）。两个界点之间的路径称为簇路径（cluster path）。方便起见，本文设每个簇中必有两个界点，称一个簇中深度较浅的界点为上界点，较深的为下界点。

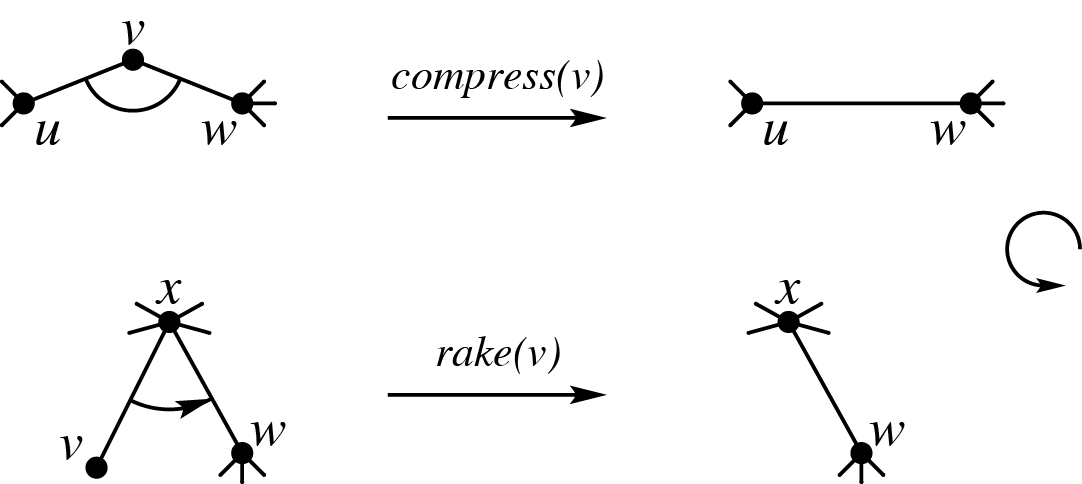
basic.png (1082×484) (uoj.ac)

（图源：@negiizhao Top tree 相关东西的理论、用法和实现，下面那张图出处相同。）

如上图所示，簇是可合并的。只要不断地执行上面两个操作就可以将整棵树合并为一个簇。簇的合并过程会形成一个二叉树的结构，我们称这棵树为 top tree。

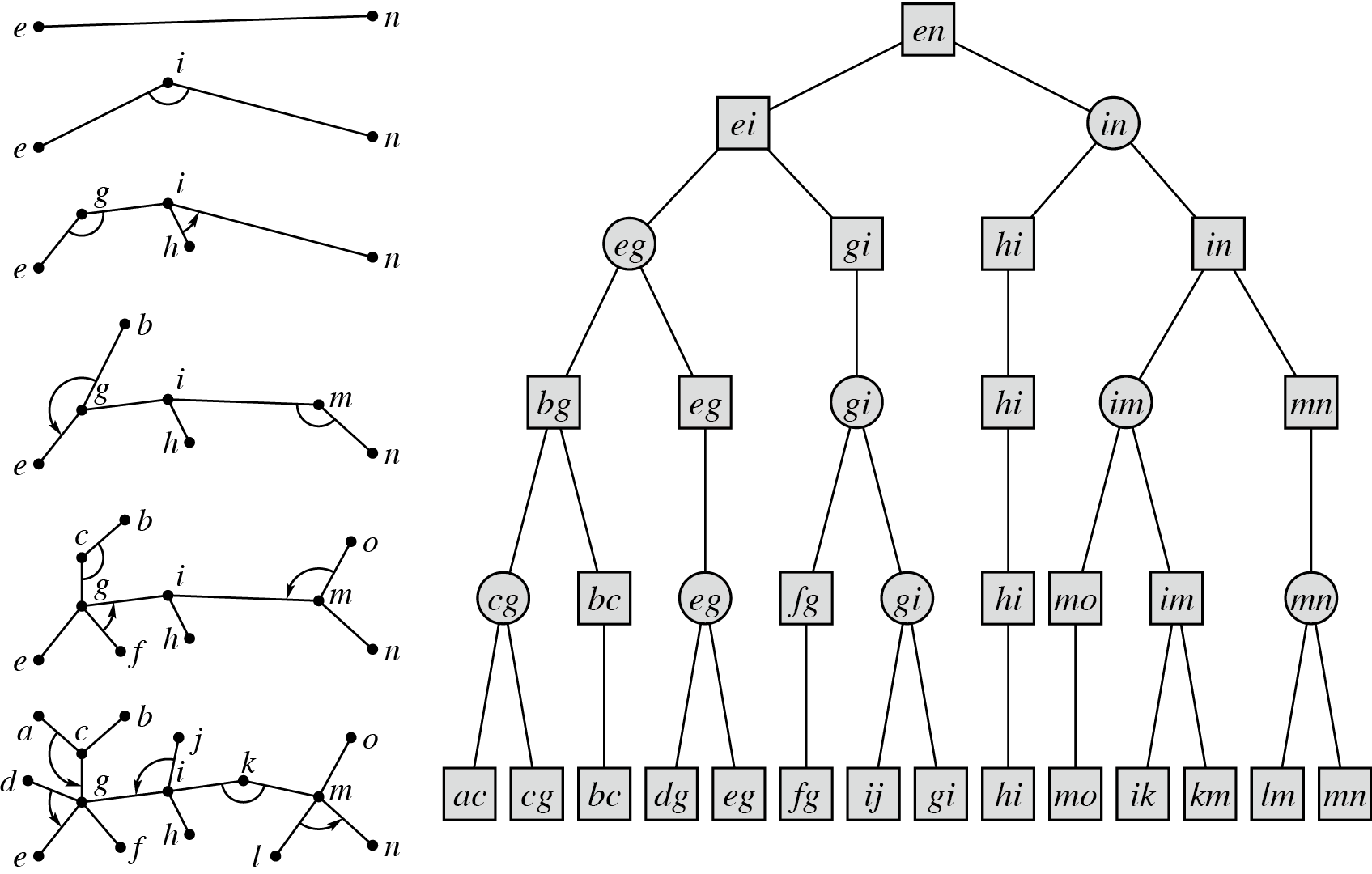
top.png (1695×1080) (uoj.ac)

Top tree 本身的实现对于树分块来说不太重要。但我们可以借用 top cluster 的理论，建立一种比常见树分块具有更多优秀性质的树分块算法。能够做到对于一棵 \(n\) 个点的树和一个块大小 \(B\)，将原树划分为 \(O\left(\dfrac{n}{B}\right)\) 个簇，每个簇的大小均为 \(O(B)\)。并且使用该算法划分出的簇满足以下性质：

不同簇的边集不相交。
一个簇的两个界点必为祖孙关系。
一个簇中的点，除界点外，其余点不会在其它簇中出现。即任意内点只可能属于一个簇。
如果一个点在多个簇中出现，那么它一定是某一个簇的下界点，同时是其余包含该点的簇的上界点。（根节点除外，因为它不可能是任何簇的下界点。）
如果把所有簇的界点作为点，每个簇的上界点向下界点连有向边，则会得到一棵有根树，称为收缩树。

以下是一个该算法的演示：

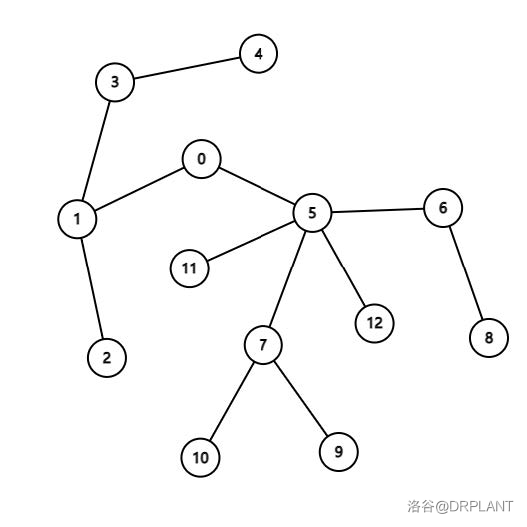
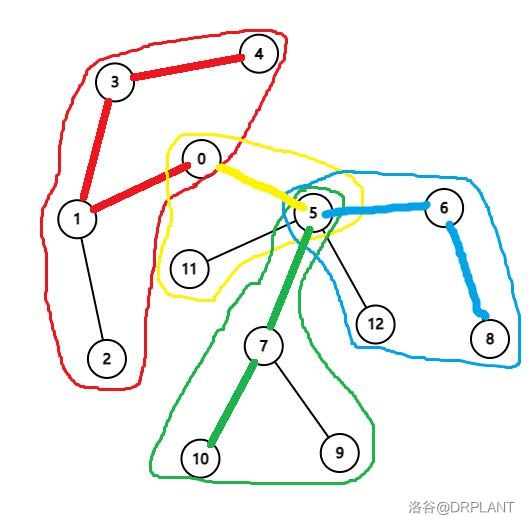
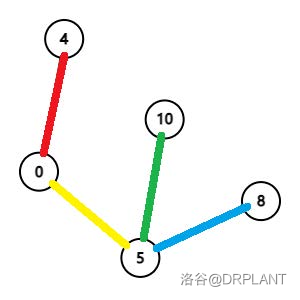
（图源：周欣《浅谈一类树分块的构建算法及其应用》）

其中图 1 为原树。图 2 为原树的一种划分，每个圈代表一个簇，彩色的边表示簇路径。图 3 为原树的收缩树。

如何实现这个算法？一个自然的想法是先建出 top tree，然后在 top tree 上截取子树。然而 top tree 的构建比较复杂，较难实现。实际上存在一种更加易于实现的静态构建算法。

算法过程

选取任意节点为根节点，并且强令根节点为一个界点。

从根节点开始 DFS，维护一个栈存储暂时还未归类的边（实际上存的是点，但代表的意义是连向其父亲的边）。当 \(u\) 要结束 DFS 时，如果发生以下 3 种情况，则要将栈中的一些边确定为若干个以 \(u\) 为上界点的簇。处理完毕后把栈中所有 \(u\) 的子树中的节点弹出。

\(u\) 为根节点。
\(u\) 有至少两个子树中存在界点。此时如果不使得 \(u\) 为界点则 \(u\) 所在簇将产生至少三个界点（\(u\) 的某个祖先将成为该簇的上界点，而 \(u\) 的子树中的界点将均成为下界点。存在两个以上的下界点显然是不合法的），所以必须令 \(u\) 为界点。
栈中剩余边（点）的数量大于 \(B\)。

下面要解决的问题是：如何合适地将 \(u\) 的子树划分为不同的簇，来满足最初的要求。考虑贪心地在栈中选取极长合法前缀作为同一个簇，直到下列情况之一发生：

\(u\) 的子树已用完。
新加入一个子树将会使当前簇中有两个下界点。
新加入一个子树将会使当前簇的大小超过 \(B\)。

全部 DFS 结束后，我们就能得到一种符合要求的划分方案。

正确性证明

显然上述算法能够保证每个簇的大小均为 \(O(B)\)。我们只需证明划分出的簇的个数为 \(O\left(\dfrac{n}{B}\right)\) 即可。换言之，只需证明上述两个部分各自 3 种情况的发生次数为 \(O\left(\dfrac{n}{B}\right)\) 即可。

对于第一部分：显然情况 1、3 发生的次数为 \(O\left(\dfrac{n}{B}\right)\)。而情况 2 只会发生在由已经找到的界点形成的虚树上，因此也是 \(O\left(\dfrac{n}{B}\right)\) 的。

对于第二部分：显然情况 1、2 只与第一部分的发生次数有关。对于情况 3，考虑将每个发生这种情况时正在划分的簇和当前做到的子树配对。则每对的未归类边数和一定大于 \(B\)，从而对数不超过 \(\dfrac{n}{B}\)，因此归于这种情况的簇的数量是 \(O\left(\dfrac{n}{B}\right)\) 的级别。

综上所述，总的划分出簇的个数为 \(O\left(\dfrac{n}{B}\right)\)，大小为 \(O(B)\)。符合上面的要求。

代码

// CL: 簇   BN: 界点   CT: 收缩树   CLP: 簇路径
int fa[maxn];  // 记录原树中的父亲
int CT_fa[maxn], near_CLP[maxn], up_BN[maxn], down_BN[maxn];
// CT_fa：每个界点在收缩树上的父亲。near_CLP：距离最近的簇路径上节点。
// up_BN：所属簇（若为界点，则其所属簇为其作为下界点时所属的簇）的上界点。down_BN：所属簇的下界点。
vector<int> BN, down_CL[maxn];  // BN：存储所有界点。down_CL：把整个簇中上界点以外的点存到下界点的 vector 中。

namespace TOP_CLUSTER {
// 放在 namespace 里面的变量是只有划分时才会用到的。
int cur_CL[maxn], cur_CL_cnt;  // 存放当前簇的临时数组。

inline void add_CL(int u, int v) {  // 新增一个以 u 为上界点，v 为下界点的簇。
  if (!v)  // 如果没有下界点，则可以任选簇中一个点作为下界点。
    v = cur_CL[cur_CL_cnt]; 
  CT_fa[v] = u, near_CLP[u] = u;
  for (int r = v; r != u; r = fa[r])
    near_CLP[r] = r;  // 预处理簇路径上每个点的最近簇路径上节点为它自己。
  for (int i = 1; i <= cur_CL_cnt; i++) {
    int r    = cur_CL[i], j;
    up_BN[r] = u, down_BN[r] = v, down_CL[v].emplace_back(r);
    for (j = r; !near_CLP[j]; j = fa[j])
      ;  // 暴跳找最近簇路径上节点，因为按 DFS 序加入栈中所以这部分复杂度可以保证。
    near_CLP[r] = near_CLP[j];
  }
  cur_CL_cnt = 0;  // 记得把存放当前簇的临时数组长度清零。
}

// ST: 栈
int ST[maxn], ST_top, rec_ST_top[maxn];  // rec_stack_top：记录 DFS 到一个节点时的栈顶。
int waiting[maxn], rec_BN[maxn];
// waiting：长存不灭的 waiting，逐渐消逝的 AC。（划掉）暂时还未归类的边。rec_BN：记录子树中最浅界点。

inline void CL_partition(int u, int FA) {  // DFS 函数
  fa[u] = FA, rec_ST_top[u] = ST_top;
  for (auto it = edge[u].begin(); it < edge[u].end(); it++)
    if (it->to == FA) {  // 先把父亲删了后面处理方便一点。
      edge[u].erase(it);
      break;
    }
  waiting[u] = 1;
  int BN_cnt = 0;  // 记录有界点的子树个数。
  for (const Edge &v : edge[u]) {
    ST[++ST_top] = v.to;
    CL_partition(v.to, u);
    waiting[u] += waiting[v.to], rec_BN[v.to] && (rec_BN[u] = rec_BN[v.to], BN_cnt++);
  }
  if (waiting[u] > B || BN_cnt > 1 || !FA) {  // 符合出栈条件
    waiting[u] = 0, rec_BN[u] = u, BN.emplace_back(u);
    for (int i = 0, j = rec_ST_top[u] + 1, cnt = 0, cur_down = 0, v; i <= edge[u].size(); i++) {
      // cnt：当前簇的大小。cur_down：当前簇的下界点。
      v = (i == edge[u].size()) ? 0 : edge[u][i].to;
      if (cnt + waiting[v] > B || (cur_down && rec_BN[v]) || !v) {  // 已无法往当前簇中再加入一个子树。
        for (; (j < rec_ST_top[v] || !v) && j <= ST_top; j++)
          cur_CL[++cur_CL_cnt] = ST[j];
        add_CL(u, cur_down), cnt = cur_down = 0;
      }
      cnt += waiting[v], rec_BN[v] && (cur_down = rec_BN[v]);
    }
    ST_top = rec_ST_top[u];  // 把栈中所有 u 的子树中的节点弹出。
    // 坑点：别写糊了把这句话写到 if 外面去了。我因为这个调了好长时间。
  }
}
}  // namespace TOP_CLUSTER

例题

P6778 [Ynoi2009] rpdq

Problem：

给定一棵 \(n\) 个节点的无根，有边权的树，每个点有个编号，编号为一个 \(1 \sim n\) 的排列。

共 \(m\) 组询问，每次询问给出 \(l,r\)，求所有点编号的二元组 \((i,j)\) 满足 \(l \le i<j \le r\) 在树上的距离的和，两个点的距离定义为连接其的简单路径上的所有边的边权和。

Solution：

显然可以将问题转化为以下式子：

\[(r-l)\sum\limits_{i=l}^r dep_i - 2 \times \sum\limits_{i=l}^r \sum\limits_{j=i+1}^r dep_{LCA(i,j)} \]

前一项可以通过前缀和简单求得，后一项看起来比较难求。

使用莫队算法。考虑 P4211 的经典结论，设 \(w_i=dep_i-dep_{fa_i}\)，\(c\left([l,r],x\right)\) 表示 \(\sum\limits_{i=l}^r dep_{LCA(i,x)}\)。这个东西可以用以下方法快速求得：将区间 \([l,r]\) 的所有节点到根的链上每个点的 \(cnt_i + 1\)，求出 \(x\) 到根的链上所有点的 \(\sum w_i \cdot cnt_i\)。以莫队右指针 \(r \rightarrow r+1\) 为例，可以把贡献差分为 \(c\left([1,r],r+1\right) - c\left([1,l-1],r+1\right)\)。这是一个经典的莫队二次离线的式子，直接套板子即可。与那道二离板子（P4887）的唯一区别是一个节点加入后会对自己产生贡献，因此求前缀和的部分要分贡献是否包含自己两种。

这样本题就解决了吗？实际上你会发现任何常见数据结构都会使 \(cnt_i + 1\) 和查询 \(\sum w_i \cdot cnt_i\) 这两部分的复杂度带上 \(\log\)。而本题带 \(\log\) 的复杂度是难以通过的。如何解决这个问题？卡常。众所周知，莫队二离可以看做对一种数据结构进行 \(O(n)\) 次修改和 \(O(n\sqrt m)\) 次查询，发现这两者是非常不平衡的。在序列上，我们一般使用分块、根号分治等平衡它们的复杂度。而本题中，我们可以使用树分块进行根号平衡。

加入一个节点时，把这个节点到根的路径拆分成以下 3 部分：

该点到最近簇路径上节点的路径。
该点的最近簇路径上节点到该簇上界点的路径。
该簇上界点到根节点的路径。（均为簇路径，可以认为是该簇上界点到根节点在收缩树上的路径。）

维护 \(val_i\) 表示节点 \(i\) 作为散块被贡献的值，\(sum1_i\) 表示每个节点 \(val_i\) 的树上前缀和，且簇与簇之间互相独立。\(val\_clp_v\) 表示某簇的下界点 \(v\) 到其上界点的这条簇路径被贡献的值，用 \(sum2_v\) 表示每个界点 \(val\_clp_v\) 的收缩树上前缀和。\(tag_v\) 表示某个下界点 \(v\) 所代表的簇作为整块被贡献的次数。修改时前两部分在原树上暴跳修改，第三部分在收缩树上暴跳修改。跳完之后更新一下 \(sum1\) 和 \(sum2\) 即可。当 \(B\) 取 \(O(\sqrt n)\) 时可以保证单次修改复杂度 \(O(\sqrt n)\)。查询时直接求 \(sum1_x + (dep_{near} - dep_{up}) \cdot tag_{down} + sum2_{up}\) 即可（\(x\) 为需要查询的节点，\(near\) 为 \(x\) 的最近簇路径上节点，\(up\) 为 \(x\) 所在簇的上界点，\(down\) 为下界点），显然是单次 \(O(1)\) 的。

这样这道题就彻底解决了。时间复杂度 \(O\left(n\left(\sqrt n + \sqrt m\right)\right)\)，空间复杂度 \(O(n+m)\)。

Core code：

这里给出本题修改以及查询部分的代码。

// 划分方式与上面相同，略。
// diff_dep[i] = dep[i] - dep[fa[i]], diff_CT_dep[i] = dep[i] - dep[CT_fa[i]];
unsigned val[maxn], val_CLP[maxn], tag[maxn], sum1[maxn], sum2[maxn];
inline void update(int x) {
  const int up = up_BN[x], down = down_BN[x];
  for (; x != near_CLP[x]; x = fa[x])
    val[x] += diff_dep[x];
  for (; x != up; x = fa[x])
    val[x] += diff_dep[x], val_CLP[down] += diff_dep[x];
  for (; CT_fa[x]; x = CT_fa[x])
    val_CLP[x] += diff_CT_dep[x], tag[x]++;
  for (int it : down_CL[down])
    sum1[it] = (down_BN[fa[it]] == down ? sum1[fa[it]] : 0) + val[it];
  for (int it : BN)
    sum2[it] = sum2[CT_fa[it]] + val_CLP[it];
}
inline unsigned query(int x) {
  const int up = up_BN[x], down = down_BN[x], near = near_CLP[x];
  return sum1[x] + (dep[near] - dep[up]) * tag[down] + sum2[up];
}

MeteorFlower's Blog