洛谷 P1027 Car的旅行路线 最短路+Dijkstra算法
题面
题目链接
题目描述
又到暑假了,住在城市A的Car想和朋友一起去城市B旅游。她知道每个城市都有4个飞机场,分别位于一个矩形的4个顶点上,同一个城市中2个机场之间有1条笔直的高速铁路,第 $ i $ 个城市中高速铁路了的单位里程价格为 $ T_i $ ,任意两个不同城市的机场之间均有航线,所有航线单位里程的价格均为 $ t $
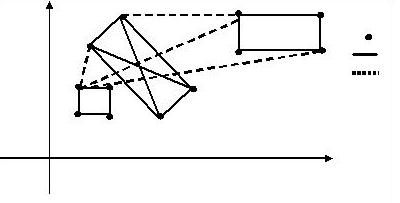
注意:图中并没有标出所有的铁路与航线。
那么Car应如何安排到城市B的路线才能尽可能的节省花费呢?她发现这并不是一个简单的问题,于是她来向你请教。
找出一条从城市A到B的旅游路线,出发和到达城市中的机场可以任意选取,要求总的花费最少。
输入输出格式
输入格式
第一行为一个正整数 $ n (0 \leq n \leq 10) $ ,表示有 $ n $ 组测试数据。
每组的第一行有4个正整数 $ s,t,A,B $
$ s (0<S \leq 100) $ 表示城市的个数, $ t $ 表示飞机单位里程的价格,A,B分别为城市A,B的序号,($ 1 \leq A,B \leq s $)。
接下来有 $ s $ 行,其中第 $ i $ 行均有7个正整数 $ xi_1,yi_1,xi_2,yi_2,xi_3,yi_3,Ti $ 这当中的 $ (xi_1,yi_1),(xi_2,yi_2),(xi_3,yi_3) $ 分别是第 $ i $ 个城市中任意3个机场的坐标, $ T_i $ 为第 $ i $ 个城市高速铁路单位里程的价格。
输出格式
共有 $ n $ 行,每行1个数据对应测试数据。 保留一位小数。
输入输出样例
输入样例
1
3 10 1 3
1 1 1 3 3 1 30
2 5 7 4 5 2 1
8 6 8 8 11 6 3
输出样例
47.5
说明
【时空限制】
1000ms,128MB
思路
首先看题,应该是个最短路题。只要把所有飞机场之间建边就可以了。但,还要处理这样一些问题
1.第四个点的位置。题中给了三个点的位置,那么就可以算出三边的长度,其中最长的那一条边一定是对角线,这样就可以计算第四个顶点的坐标了
2.建边的长度。如果两个飞机场是一个城市的,那么边的长度(费用)是这个城市高铁费用乘上实际长度;否则是飞机费乘实际长度
3.这道题可以从A的任意机场出发,到任意一个B的机场就终止。那么怎么变成单源最短路径呢?那么实际上可以将初始城市的四个点变成一个,也就是将他们之间的长度都变成0,再跑最短路就可以了
AC代码
#include<bits/stdc++.h>
const int maxn=105;
using namespace std;
int s,t,a,b;
struct City
{
int x[4],y[4];
int T;
}C[maxn];
int tot,to[maxn*maxn],nxt[maxn*maxn],head[maxn];
double d[maxn*maxn],ans[maxn*4];
bool vis[maxn*4];
priority_queue< pair<double,int> > q;
void Get0(int p)
{
City &q=C[p];
double l1=sqrt(((q.x[1])-(q.x[2]))*((q.x[1])-(q.x[2]))+((q.y[1])-(q.y[2]))*((q.y[1])-(q.y[2])));
double l2=sqrt(((q.x[1])-(q.x[3]))*((q.x[1])-(q.x[3]))+((q.y[1])-(q.y[3]))*((q.y[1])-(q.y[3])));
double l3=sqrt(((q.x[2])-(q.x[3]))*((q.x[2])-(q.x[3]))+((q.y[2])-(q.y[3]))*((q.y[2])-(q.y[3])));
double maxl=max(l1,max(l2,l3));
if(maxl==l1) q.x[0]=q.x[1]+q.x[2]-q.x[3],q.y[0]=q.y[1]+q.y[2]-q.y[3];
if(maxl==l2) q.x[0]=q.x[1]+q.x[3]-q.x[2],q.y[0]=q.y[1]+q.y[3]-q.y[2];
if(maxl==l3) q.x[0]=q.x[2]+q.x[3]-q.x[1],q.y[0]=q.y[2]+q.y[3]-q.y[1];
}
void Add(int u,int v,double len)
{
to[++tot]=v;nxt[tot]=head[u];head[u]=tot;d[tot]=len;
to[++tot]=u;nxt[tot]=head[v];head[v]=tot;d[tot]=len;
}
void Dijkstra()
{
for(int i=0;i<4*s;i++) ans[i]=99999999;
ans[4*a]=0;ans[4*a+1]=0;ans[4*a+2]=0;ans[4*a+3]=0;
memset(vis,0,sizeof(vis));
q.push(make_pair(0,4*a));
q.push(make_pair(0,4*a+1));
q.push(make_pair(0,4*a+2));
q.push(make_pair(0,4*a+3));
while(!q.empty())
{
int u=q.top().second;q.pop();
if(vis[u]) continue;
vis[u]=true;
for(int i=head[u];i;i=nxt[i])
{
int v=to[i];
if(ans[u]+d[i]<ans[v])
{
ans[v]=ans[u]+d[i];
q.push(make_pair(-ans[v],v));
}
}
}
}
void work()
{
scanf("%d%d%d%d",&s,&t,&a,&b);--a,--b;
for(int i=0;i<s;i++)
{
City &q=C[i];
scanf("%d%d%d%d%d%d%d",&q.x[1],&q.y[1],&q.x[2],&q.y[2],&q.x[3],&q.y[3],&q.T);
}
for(int i=0;i<s;i++) Get0(i);
double len;
for(int i=0,no1,no2,air1,air2;i<4*s;i++)
{
for(int j=0;j<4*s;j++)
{
no1=i/4;no2=j/4;air1=i%4;air2=j%4;
len=sqrt((C[no1].x[air1]-C[no2].x[air2])*(C[no1].x[air1]-C[no2].x[air2])+(C[no1].y[air1]-C[no2].y[air2])*(C[no1].y[air1]-C[no2].y[air2]));
if(no1==no2 && no1==a) len*=0;
else if(no1==no2) len*=C[no1].T;
else len*=t;
Add(i,j,len);
}
}
Dijkstra();
printf("%.1f\n",min(ans[b*4],min(ans[b*4+1],min(ans[b*4+2],ans[b*4+3]))));
}
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++) work();
return 0;
}
总结
第四个点的处理算是一个小问题,还有将起点城市的四个点变成一个



