洛谷 P3958 奶酪并查集

题面
总结

题面

题目链接

题面

题目描述

现有一块大奶酪，它的高度为 $ h $ ，它的长度和宽度我们可以认为是无限大的，奶酪中间有许多半径相同的球形空洞。我们可以在这块奶酪中建立空间坐标系，在坐标系中，奶酪的下表面为 $ z=0 $ ，奶酪的上表面为 $ z=h $ 。

现在，奶酪的下表面有一只小老鼠 Jerry，它知道奶酪中所有空洞的球心所在的坐标。如果两个空洞相切或是相交，则 Jerry 可以从其中一个空洞跑到另一个空洞，特别地，如果一个空洞与下表面相切或是相交，Jerry 则可以从奶酪下表面跑进空洞；如果一个空洞与上表面相切或是相交，Jerry 则可以从空洞跑到奶酪上表面。

位于奶酪下表面的 Jerry 想知道，在不破坏奶酪的情况下，能否利用已有的空洞跑到奶酪的上表面去?

空间内两点 $ P_1(x_1,y_1,z_1),P_2(x_2,y_2,z_2) $ 的距离公式是：

\[dist(P_1,P_2)= \sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2} \]

输入输出格式

输入格式

每个输入文件包含多组数据。

的第一行，包含一个正整数 $ T $ ，代表该输入文件中所含的数据组数。

接下来是 $ T $ 组数据，每组数据的格式如下：第一行包含三个正整数 $ n,h $ 和 $ r $，两个数之间以一个空格分开，分别代表奶酪中空洞的数量，奶酪的高度和空洞的半径。

接下来的 $ n $ 行，每行包含三个整数 $ x,y,z $ ，两个数之间以一个空格分开，表示空洞球心坐标为 $ (x,y,z) $ 。

输出格式：

$ T $ 行，分别对应 $ T $ 组数据的答案，如果在第 $ i $ 组数据中，Jerry 能从下表面跑到上表面，则输出Yes，如果不能，则输出No （均不包含引号）。

输入输出样例

输入样例

输出样例

Yes
No
Yes
'```

##说明

【输入输出样例说明】

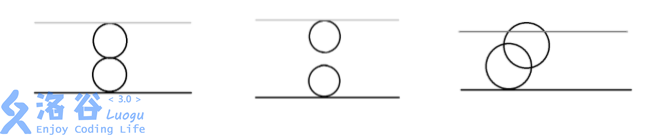
![](https://cdn.luogu.org/upload/pic/10860.png)

第一组数据,由奶酪的剖面图可见：

第一个空洞在(0,0,0)(0,0,0)与下表面相切

第二个空洞在(0,0,4)(0,0,4)与上表面相切 两个空洞在(0,0,2)(0,0,2)相切

输出 Yes

第二组数据,由奶酪的剖面图可见：

两个空洞既不相交也不相切

输出 No

第三组数据,由奶酪的剖面图可见：

两个空洞相交 且与上下表面相切或相交

输出 Yes

【数据规模与约定】

对于 20% 的数据, $ n=1,1 \leq h,r \leq 10,000 $ ，坐标的绝对值不超过 10,000。

对于 40% 的数据, $ 1 \leq n \leq 8,1 \leq h,r \leq 10,000 $ ,坐标的绝对值不超过 10,000。

对于 80% 的数据,  $ 1 \leq n \leq 1,000,1 \leq h,r \leq 10,000 $ ,坐标的绝对值不超过 10,000。

对于 100% 的数据, $ 1 \leq n \leq 1,000,1 \leq h,r \leq 1,000 , T \leq 20 $ ,坐标的 绝对值不超过 1,000,000,000。

【时空限制】

1000ms,256MB

#思路

这一题可以先找出所有的连通块，这个可以用并查集来实现。然后找出与底端连通和顶端连通的洞，依次配对，如果父亲是一样的，证明有一条路径可以从底端到顶端

#AC代码

```cpp
#include<bits/stdc++.h>
const long long maxn=1005;
using namespace std;

long long n,h,r;
long long x[maxn],y[maxn],z[maxn];
long long fa[maxn];

long long FF(long long p)
{
    if(p!=fa[p]) {fa[p]=FF(fa[p]);}
    return fa[p];
}

void Merge(long long a,long long b)
{
    long long f1=FF(a);
    long long f2=FF(b);
    if(f1!=f2) fa[f1]=f2;
}

bool can(long long i,long long j)
{
    double len=sqrt((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j])+(z[i]-z[j])*(z[i]-z[j]));
    return len<=2*r;
}

void work()
{
    scanf("%lld%lld%lld",&n,&h,&r);
    for(long long i=1;i<=n;i++) scanf("%lld%lld%lld",&x[i],&y[i],&z[i]);
    for(long long i=1;i<=n;i++) fa[i]=i;
    for(long long i=1;i<=n;i++)
        for(long long j=i+1;j<=n;j++)
            if(can(i,j)) Merge(i,j);
    for(long long i=1;i<=n;i++)
    if(z[i]<=r)
    {
        for(long long j=1;j<=n;j++)
        if(z[j]+r>=h)
        {
            if(FF(i)==FF(j))
            {
                printf("Yes\n");
                return;
            }
        }
    }
    printf("No\n");
    return;
}

int main()
{
    long long t;
    scanf("%lld",&t);
    for(long long i=1;i<=t;i++) work();
    return 0;
}

总结

这题还是有几个坑。

1.多组数据，要初始化 2.Yes，No注意大小写 3.要开long long

posted @ 2018-10-09 16:42 Mercury04 阅读(277) 评论(0) 编辑收藏举报

刷新页面返回顶部

Mercury04

洛谷 P3958 奶酪 并查集

题面