洛谷 P2486 [SDOI2011]染色 树链剖分
题面
题目链接
题目描述

输入输出格式
输入格式

输出格式
对于每个询问操作,输出一行答案。
输入输出样例
输入样例:
6 5
2 2 1 2 1 1
1 2
1 3
2 4
2 5
2 6
Q 3 5
C 2 1 1
Q 3 5
C 5 1 2
Q 3 5
输出样例:
3
1
2
说明
【数据规模】
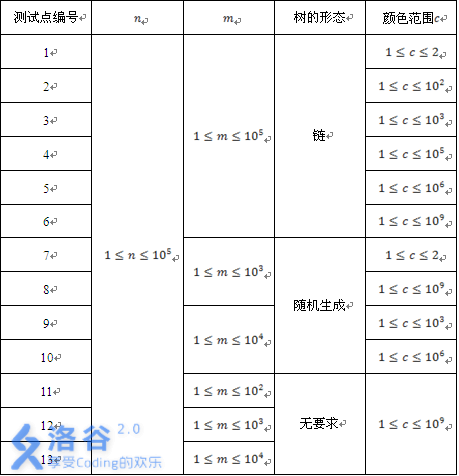

【时空限制】
1000ms,128M
思路
看题,操作从a到b的路径上所有点,可以想到树剖。
然而这一题要求的结果有点迷,如果是线段树,第一感觉是要用线段树合并。结构体里面保存 最左端的颜色nowl 和 最右端的颜色nowr ,在两个线段树合并时, 该区间内颜色段数量sum 需要作一下判断:如果左儿子的最右端和右儿子的最左端颜色相同,那么sum应该是左儿子和右儿子的sum之和减1;否则是左儿子和右儿子的sum之和。
基本思路确定了,再看看实际。。。
PushDown与Update
void Update(int p)
{
s(p)=s(p<<1)+s(p<<1|1);
if(nr(p<<1)==nl(p<<1|1)) s(p)--; ///如上所说的判断
nl(p)=nl(p<<1);
nr(p)=nr(p<<1|1);
}
void PushDown(int p)
{
if(t(p))
{
s(p<<1)=s(p<<1|1)=1; ///此时两个儿子的sum都是1
nl(p<<1)=nr(p<<1)=nl(p<<1|1)=nr(p<<1|1)=t(p<<1)=t(p<<1|1)=t(p); ///左、右儿子最左、最右结点,还有懒标记全部变成了现在染上的颜色
t(p)=0;
}
}
Q
本来以为查询操作也是线段树合并,然后写了一半发现不对劲,因为查询的路径上新给定的标号nid是不连续的!不过,nid不连续,我们可以直接判断。
int Ask2(int u,int v)
{
int ans=0;
while(top[u]!=top[v])
{
if(dep[top[u]]<dep[top[v]]) swap(u,v);
SegmentTree tmp=Ask1(1,nid[top[u]],nid[u]);
ans+=tmp.sum; ///统计答案的时候把单独的这条链的颜色段数量加上
if(tmp.nl==Ask1(1,nid[fa[top[u]]],nid[fa[top[u]]]).nr) ans--; ///考虑到,如果这条链可以和下一条链合并,那必然是他和他的父亲合并,所以这个时候只要判断他和他父亲颜色是否相同,来判断是否要减1
u=fa[top[u]];
}
if(dep[u]>dep[v]) swap(u,v);
ans+=Ask1(1,nid[u],nid[v]).sum;
return ans;
}
AC代码
#include<bits/stdc++.h>
const int maxn=100010;
using namespace std;
int n,m,wt[maxn];
int tot,to[maxn<<1],nxt[maxn<<1],head[maxn];
int son[maxn],fa[maxn],len[maxn],dep[maxn];
int cnt,nid[maxn],nw[maxn],top[maxn];
struct SegmentTree
{
int l,r,sum,nl,nr,tag;
#define l(a) tree[a].l
#define r(a) tree[a].r
#define m(a) ((l(a)+r(a))>>1)
#define len(a) (r(a)-l(a)+1)
#define s(a) tree[a].sum
#define nl(a) tree[a].nl
#define nr(a) tree[a].nr
#define t(a) tree[a].tag
}tree[maxn<<2];
void dfs1(int u,int f,int d)
{
fa[u]=f;dep[u]=d;len[u]=1;
for(int i=head[u];i;i=nxt[i])
{
int v=to[i];
if(v==f) continue;
dfs1(v,u,d+1);
len[u]+=len[v];
if(len[v]>len[son[u]]) son[u]=v;
}
}
void dfs2(int p,int t)
{
nid[p]=++cnt;
nw[cnt]=wt[p];
top[p]=t;
if(!son[p]) return;
dfs2(son[p],t);
for(int i=head[p];i;i=nxt[i])
{
int v=to[i];
if(v==fa[p] || v==son[p]) continue;
dfs2(v,v);
}
}
void Update(int p)
{
s(p)=s(p<<1)+s(p<<1|1);
if(nr(p<<1)==nl(p<<1|1)) s(p)--;
nl(p)=nl(p<<1);
nr(p)=nr(p<<1|1);
}
void BuildTree(int p,int l,int r)
{
l(p)=l;r(p)=r;
if(l==r)
{
s(p)=1;
nl(p)=nr(p)=nw[l];
return;
}
BuildTree(p<<1,l,m(p));
BuildTree(p<<1|1,m(p)+1,r);
Update(p);
}
void PushDown(int p)
{
if(t(p))
{
s(p<<1)=s(p<<1|1)=1;
nl(p<<1)=nr(p<<1)=nl(p<<1|1)=nr(p<<1|1)=t(p<<1)=t(p<<1|1)=t(p);
t(p)=0;
}
}
void Change1(int p,int l,int r,int k)
{
if(l<=l(p) && r>=r(p))
{
s(p)=1;
nl(p)=nr(p)=t(p)=k;
return;
}
PushDown(p);
if(l<=m(p)) Change1(p<<1,l,r,k);
if(r>m(p)) Change1(p<<1|1,l,r,k);
Update(p);
}
void Change2(int u,int v,int k)
{
while(top[u]!=top[v])
{
if(dep[top[u]]<dep[top[v]]) swap(u,v);
Change1(1,nid[top[u]],nid[u],k);
u=fa[top[u]];
}
if(dep[u]>dep[v]) swap(u,v);
Change1(1,nid[u],nid[v],k);
}
SegmentTree Ask1(int p,int l,int r)
{
if(l<=l(p) && r>=r(p)) return tree[p];
PushDown(p);
if(r<=m(p)) return Ask1(p<<1,l,r);
else if(l>m(p)) return Ask1(p<<1|1,l,r);
else
{
SegmentTree a=Ask1(p<<1,l,r),b=Ask1(p<<1|1,l,r),tmp;
tmp.nl=a.nl;tmp.nr=b.nr;
tmp.sum=a.sum+b.sum;
if(a.nr==b.nl) tmp.sum--;
return tmp;
}
}
int Ask2(int u,int v)
{
int ans=0;
while(top[u]!=top[v])
{
if(dep[top[u]]<dep[top[v]]) swap(u,v);
SegmentTree tmp=Ask1(1,nid[top[u]],nid[u]);
ans+=tmp.sum;
if(tmp.nl==Ask1(1,nid[fa[top[u]]],nid[fa[top[u]]]).nr) ans--;
u=fa[top[u]];
}
if(dep[u]>dep[v]) swap(u,v);
ans+=Ask1(1,nid[u],nid[v]).sum;
return ans;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&wt[i]);
for(int i=1;i<n;i++)
{
int u,v;scanf("%d%d",&u,&v);
to[++tot]=v;nxt[tot]=head[u];head[u]=tot;
to[++tot]=u;nxt[tot]=head[v];head[v]=tot;
}
dfs1(1,1,1);
dfs2(1,1);
BuildTree(1,1,n);
for(int i=1;i<=m;i++)
{
char ch;cin>>ch;
int u,v,k;scanf("%d%d",&u,&v);
if(ch=='C')
{
scanf("%d",&k);
Change2(u,v,k);
}
else printf("%d\n",Ask2(u,v));
}
return 0;
}
总结与拓展
感觉有点没讲清楚。这道题写完应该是对树剖有了进一步的巩固。



