20221113_T3B_问题转化二分

题意

魔术师小 Q 正在和小朋友们玩一个游戏。有 \(n\) 顶外形相同的魔术帽和一个魔术球，游戏开始前，小 Q 会将魔术帽倒扣放置排成一排，这些魔术帽从左到右依次编号为 \(1,2,...,n\)。
每一局游戏，小 Q 会先将魔术球放在其中一顶魔术帽底下，然后进行若干次交换，每次交换时小 Q 将选出两顶魔术帽，交换它们的位置。整个过程对于小朋友们而言都是可见的。交换结束后，小 Q 让小朋友们打开放有魔术球的魔术帽，正确找到魔术球则游戏胜利。
为了进行多局游戏，魔术师小 Q 准备了一个长度为 m 的操作序列 \((a_1, b_1),(a_2,b_2),...,(a_m,b_m)\)，其中 \((a_i,b_i)\) 表示交换 \(a_i\) 号和 \(b_i\) 号魔术帽（若 \(a_i=b_i\) 则不交换）。之后，小 Q 和小朋友们玩 \(q\) 局游戏。其中，第 \(j\) 轮游戏，小 Q 会先将魔术球放在 \(x_j\) 号魔术帽下，然后进行操作序列中 \([l_j,r_j]\) 这个片段，即依次进行交换 \((al_j,bl_j),(al_j+1,bl_j+1),...,(al_j, br_j)\)。请求出每次游戏交换结束时，魔术球位于在哪一顶魔术帽下。
注意：这里的魔术帽编号始终是按照位置. 从左到右编号的，即每次交换魔术帽之后，所有魔术帽会按照从左到右的顺序重新编号为 \(1,2,...,n\)。

题解

赛事得分：0/100/100

阴间题

我们考虑建图，如果要交换两个东西，我们就把东西交换相连。

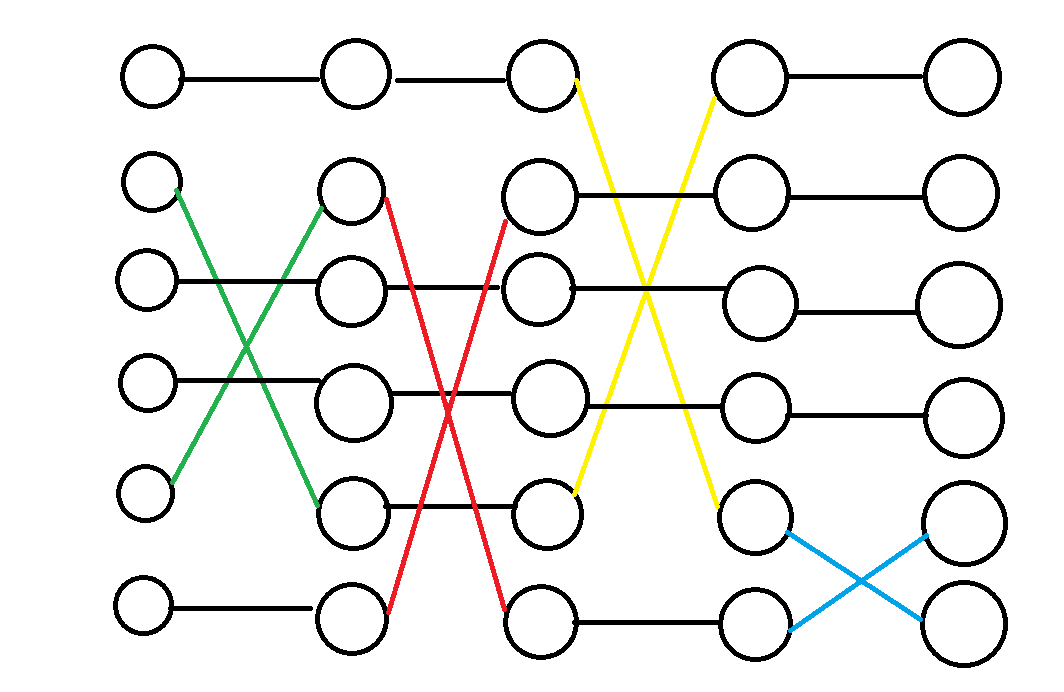
上面是一张当有 4 轮操作时候的图，我们发现如果我们知道开始的时候东西在哪里，然后沿着 \([l,r]\) 轮的路线走下去就好了。

但是这样的复杂度是 \(\mathcal{O}(nm)\) 的，并且需要倍增，非常难办。

不过我们发现，我们大多数的边都是从左边一个直接递给下一个的。所以非常浪费，真正有用的边一共只有 \(m\) 条，我们直接把没有用的边删掉，直接把这个盒子上一次的操作连向下一个操作。

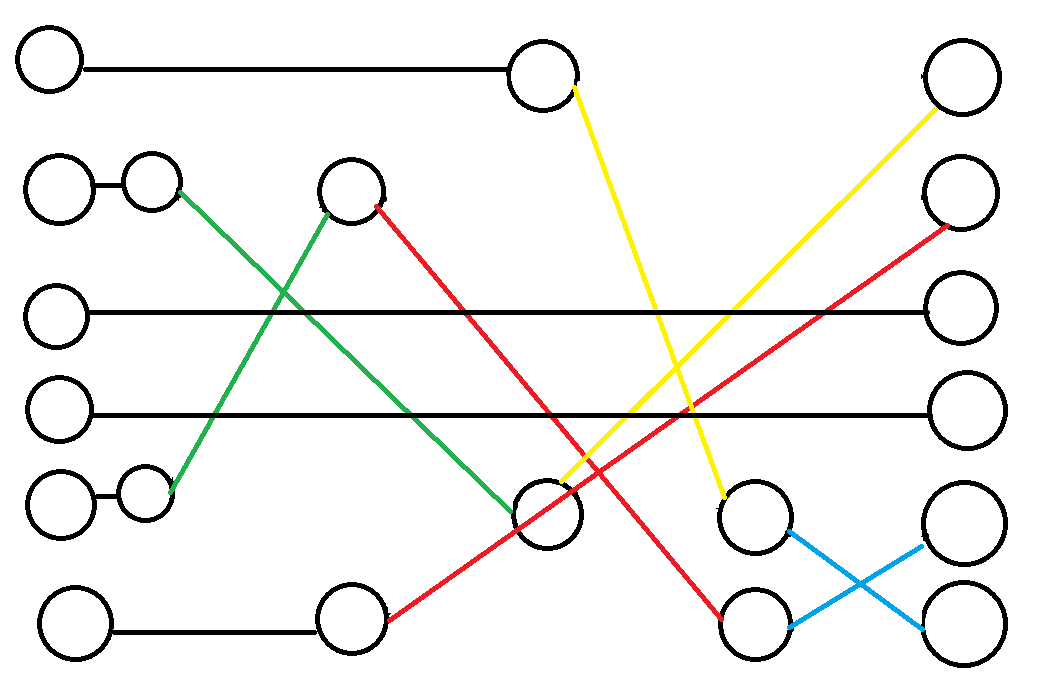
画了 8 min，上面那个图就可以简化成这个图。

因为我们要处理 \([l,r]\) 的问题，我们可以转化成先从 \(l\) 到 \(1\)，然后再从 \(1\) 到 \(r\)。我们只需要建一个反图就好了。

那么怎么查询 \(k\) 步之后在哪呢？

我们发现我们之前省略的点为什么省略就是因为他跟前面一个点答案不变，所以我们记录一下这些点的时间，然后二分查询就好了。

代码

#include <bits/stdc++.h>
using namespace std;
template <typename T>inline void read(T& t){t=0; register char ch=getchar(); register int fflag=1;while(!('0'<=ch&&ch<='9')) {if(ch=='-') fflag=-1;ch=getchar();}while(('0'<=ch&&ch<='9')){t=t*10+ch-'0'; ch=getchar();} t*=fflag;}
template <typename T,typename... Args> inline void read(T& t, Args&... args) {read(t);read(args...);}
const int N = 1e5 + 10, inf = 0x3f3f3f3f;

int n, m, q, a[N], b[N], cnt, id[N];
vector<pair<int, int> >G[N], rG[N];

int main() {
    read(n, m, q);
    for(int i = 1; i <= m; ++i) read(a[i], b[i]);
    for(int i = 1; i <= n; ++i) id[i] = i, G[i].push_back(make_pair(0, i));
    for(int i = 1; i <= m; ++i) {
        G[id[a[i]]].push_back(make_pair(i, b[i]));
        G[id[b[i]]].push_back(make_pair(i, a[i]));
        swap(id[a[i]], id[b[i]]);
    }
    for(int i = 1; i <= n; ++i)
        for(auto [u, v] : G[i]) rG[v].push_back(make_pair(u, i));
    for(int i = 1; i <= n; ++i) sort(rG[i].begin(), rG[i].end());
    for(int i = 1; i <= q; ++i) {
        int x, l, r;
        read(x, l, r);
        int left = 0, right = rG[x].size() - 1, p, ans;
        while(left <= right) {
            int mid = left + right >> 1;
            if(rG[x][mid].first == l - 1) {
                p = rG[x][mid].second;
                break;
            }
            if(rG[x][mid].first >= l) right = mid - 1;
            else {
                left = mid + 1;
                p = rG[x][mid].second;
            }
        }
        left = 0, right = G[p].size() - 1;
        while(left <= right) {
            int mid = left + right >> 1;
            if(G[p][mid].first == r) {
                ans = G[p][mid].second;
                break;
            }
            if(G[p][mid].first > r) right = mid - 1;
            else {
                ans = G[p][mid].second;
                left = mid + 1;
            }
        }
        cout << ans << endl;
    }
    return 0;
}