20221111_T1B_线段树优化建图/并查集

题意

给定一个字符串，其中只有 a 和 b，现在一个字符能够跳到与之中间 a 的个数范围在 \([l,r]\) 的东西。

题解

赛时得分：100/100

对于一个东西，显然如果将能相互到达连边，那么一个点肯定是向后面和前面的一个区间连边的。

这个区间得到，我们可以通过二分解决。

普通是暴力枚举这些东西然后用并查集合并。这样复杂度显然是 \(\mathcal{O}(n^2)\) 的。我们思考线段树优化建图（毕竟是一个区间）

看如下图建边过程

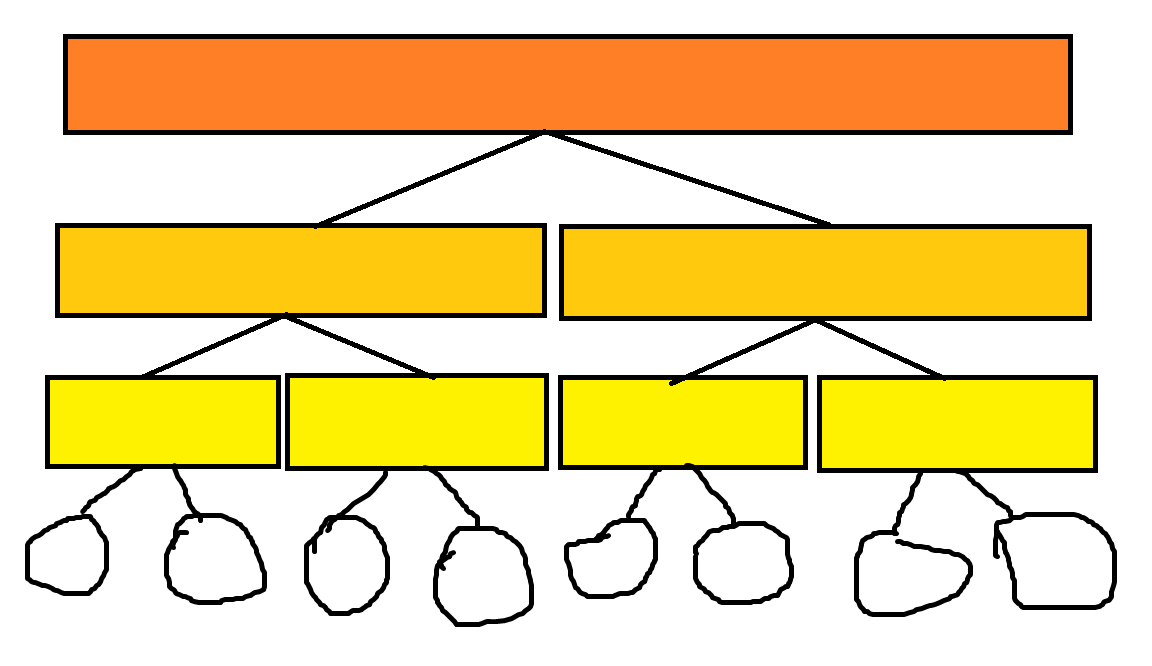
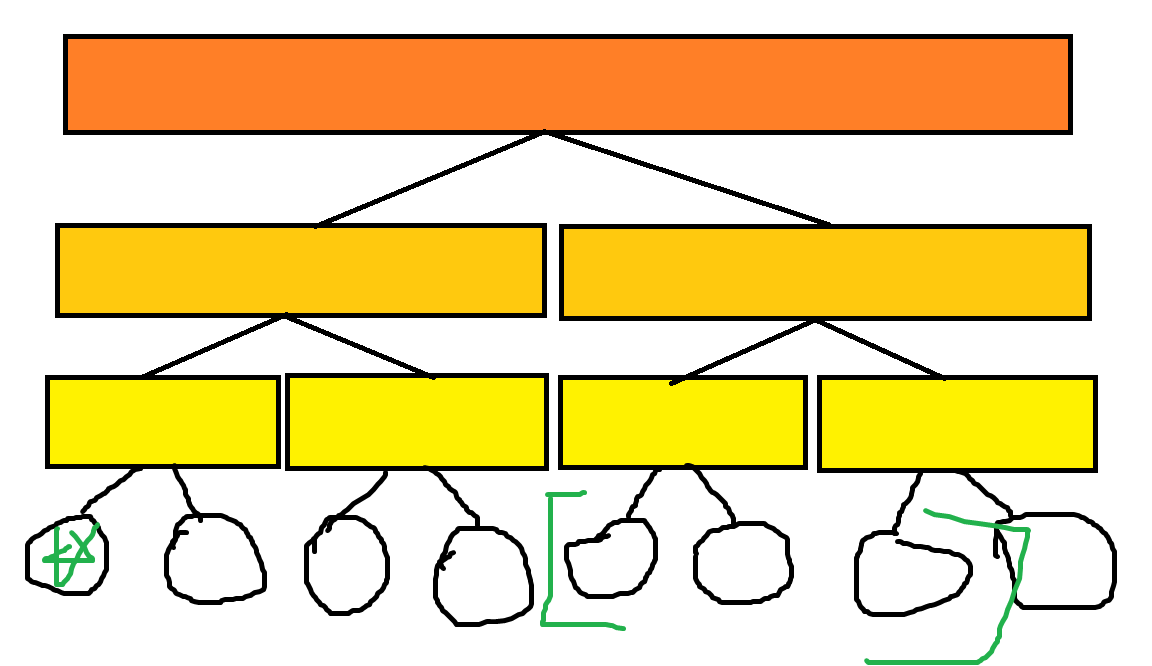
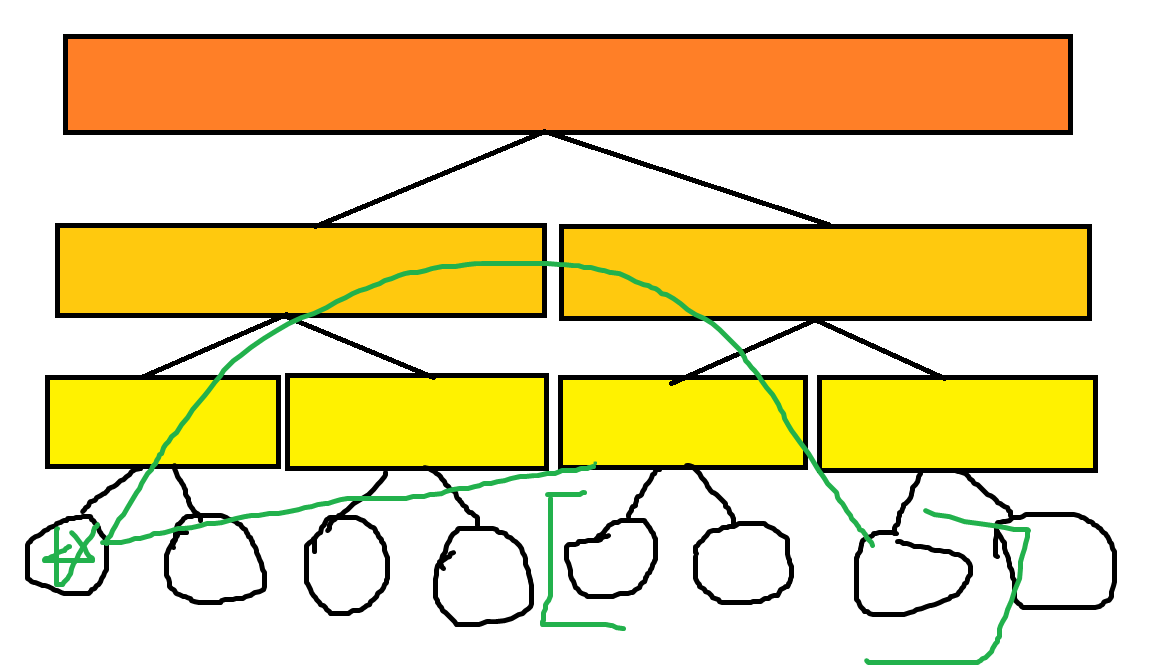
这样建图之后我们满足了建图复杂度是 \(\mathcal{O}(n\log n)\) 但是怎么查询呢？

我们发现我们建边只会是一个点向另一个点或者是方框建边，那么我们固定一个点，另一个点向上跳，看看有没有固定在一起的就好了。

所以总时间复杂度 \(\mathcal{O}(n\log n)\)。

题解是 \(\mathcal{O}(n)\) 是根据 \(k\) 的大小分类。我不会，爬了。

出题人说这方法只有 45 分，但是卡不掉。

代码

#include <bits/stdc++.h>
using namespace std;
template <typename T>inline void read(T& t){t=0; register char ch=getchar(); register int fflag=1;while(!('0'<=ch&&ch<='9')) {if(ch=='-') fflag=-1;ch=getchar();}while(('0'<=ch&&ch<='9')){t=t*10+ch-'0'; ch=getchar();} t*=fflag;}
template <typename T,typename... Args> inline void read(T& t, Args&... args) {read(t);read(args...);}
const int N = 2e6 + 10, inf = 0x3f3f3f3f;

int n, l, r, q, sum[N], lc[N << 2], rc[N << 2], id[N << 2];
string st;
int fa[N << 2], rnk[N << 2];
bool biao[N << 2];

inline int findf(int x) {
    if(fa[x] == x) return x;
    else return fa[x] = findf(fa[x]);
}
inline void merge(int x, int y) {
    int fx = findf(x), fy = findf(y);
    if(fx == fy) return;
    if(rnk[fx] >= rnk[fy]) swap(fx, fy), swap(x, y);
    fa[fx] = fy; rnk[fy] += fx;
} 
inline bool check(int x, int y) {return findf(x) == findf(y);}
inline void build(int u, int l, int r) {
    // u 就是这个点的标号了
    lc[u] = l, rc[u] = r;
    if(l == r) {
        id[l] = u;
        return;
    }
    int mid = l + r >> 1;
    build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
}
inline void adde(int u, int l, int r, int idu) {
    if(l <= lc[u] && r >= rc[u]) {
        merge(u, idu);
        biao[u] = 1;
        return;
    }
    if(l > rc[u] || lc[u] > r) return;
    adde(u << 1, l, r, idu), adde(u << 1 | 1, l, r, idu);
}
inline bool Find(int u, int idu) {
    if(findf(u) == findf(idu)) return 1;
    else if(u != 1) return Find(u >> 1, idu);
    return 0;
}
inline bool upup(int u1, int u2) {
    if(u1 == 1) return 0;
    if(u1 != u2) return upup(u1 >> 1, u2 >> 1);
    else if(biao[u1]) return 1;
    else return upup(u1 >> 1, u2 >> 1);
}
inline void Down(int u) {
    if(lc[u] == rc[u]) return;
    if(fa[u] != u) merge(u, u << 1), merge(u << 1, u << 1 | 1);
    Down(u << 1), Down(u << 1 | 1);
    return;
}

int main() {
    freopen("virtual.in", "r", stdin);
    freopen("virtual.out", "w", stdout);
    cin >> n >> l >> r;
    cin >> st;
    st = '*' + st;
    for(int i = 1; i <= n; ++i) sum[i] = sum[i - 1] + (st[i] == 'a');
    build(1, 1, n);
    for(int i = 1; i <= (n << 2); ++i) fa[i] = i, rnk[i] = 1;
    for(int i = 1; i <= n; ++i) {
        int Le = lower_bound(sum + 1, sum + n + 1, l + sum[i - 1]) - sum, Ri = upper_bound(sum + 1, sum + n + 1, r + sum[i - 1]) - sum - 1;
        if(Le <= Ri) adde(1, Le, Ri, id[i]);
        Le = lower_bound(sum, sum + n + 1, sum[i] - r) - sum + 1, Ri = lower_bound(sum, sum + n + 1, sum[i] - l + 1) - sum;
        if(Le <= Ri) adde(1, Le, Ri, id[i]);
    }
    // }
    Down(1);
    read(q);
    for(int i = 1; i <= q; ++i) {
        int x, y;
        read(x, y);
        if(Find(id[x], id[y]) || Find(id[y], id[x])) puts("Yes");
        else puts("No");
    } 
    return 0;
}