二维数点的研究
二维数点的原问题
给定 \(n\) 个点 \((x_i,y_i)\) 给出 \(m\) 个矩形,求在矩形中有多少个点。
解题方法
这个原问题还是比较好解决的,我们先把问题转化一下。
我们要求的就是 \(\begin{cases}l_j\leq x_i\leq r_j\\ d_j \leq y_i\leq u_j\end{cases}\) 的满足条件的 \(i\) 的个数。
我们先做一步转化,原来的问题要满足 \(4\) 个条件,太多了,我们拆成 \(2\) 个条件。怎么拆成两个条件呢?我们既然要求一个矩形中的,我们就小容斥把它容斥掉就好了,先加上右上角的点的左下部分,然后减去左上的点的左下部分,再减去右下的点的左下部分,再加上左下的点的左下部分。这就是一个小容斥。
然后我们就只要求类似于下图的一个问题了。就是虚线的红框里有多少点。
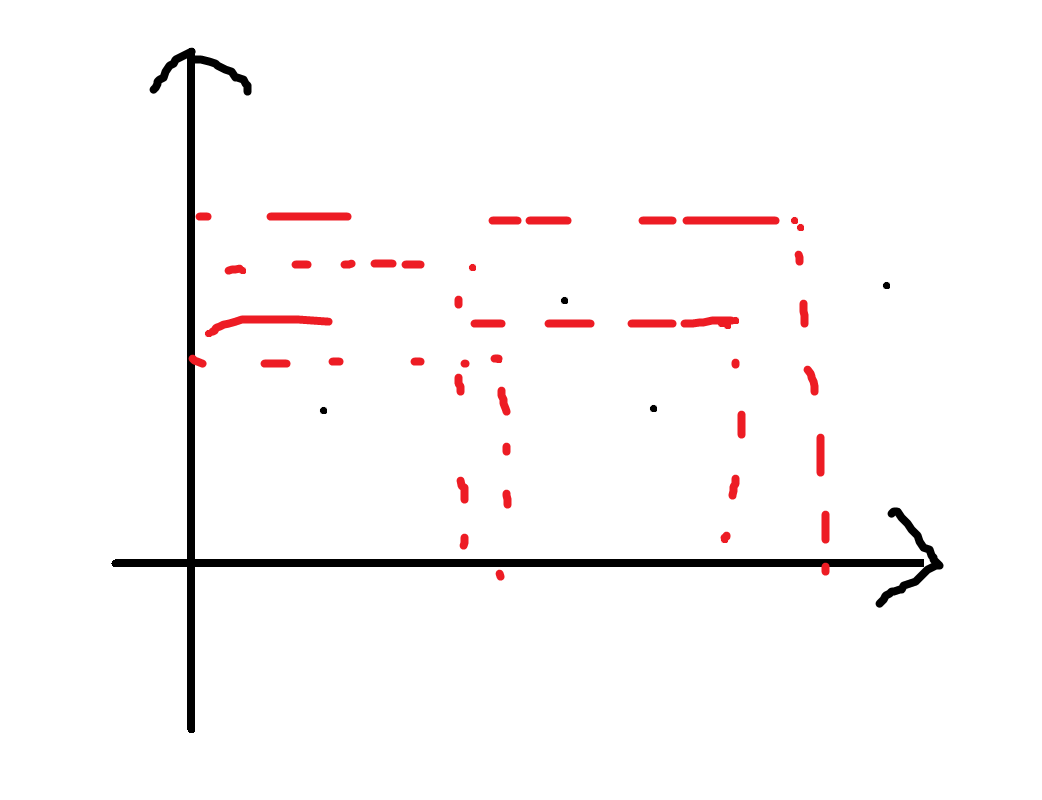
这个问题不是很难,我们把每个点想成一个事件。我们先把这些事件按照 \(y\) 排序,然后对于每个要查询的点,我们已经确定了在这个查询点下面的东西之前已经搜过了,我们现在只要满足在他左边的条件了,那么很简单,开一个树状数组就可以解决问题。对于一个黑色的点,我们就在树状数组里记一下他的位置,然后用树状数组查询一下就好了。
代码
点击查看代码
#include <bits/stdc++.h>
using namespace std;
template <typename T>inline void read(T& t){t=0; register char ch=getchar(); register int fflag=1;while(!('0'<=ch&&ch<='9')) {if(ch=='-') fflag=-1;ch=getchar();}while(('0'<=ch&&ch<='9')){t=t*10+ch-'0'; ch=getchar();} t*=fflag;}
template <typename T,typename... Args> inline void read(T& t, Args&... args) {read(t);read(args...);}
const int N = 5e5 + 10, inf = 0x3f3f3f3f;
int n, q, ans[N], m;
vector<int>vx;
vector<array<int,4> >event;
struct BIT {
int a[N];
void update(int u, int va = 1) {for(; u <= m; u += u & (-u)) a[u] += va;}
int Query(int u) {
int res = 0;
for(; u; u -=u & (-u)) res += a[u];
return res;
}
}b;
int main() {
read(n, q);
for(int i = 1; i <= n; ++i) {
int x, y;
read(x, y);
vx.push_back(x);
event.push_back({y, 0, x});
}
for(int i = 1; i <= q; ++i) {
int x1, x2, y1, y2;
read(x1, y1, x2, y2);
event.push_back({y2, 1, x2, i});
event.push_back({y1 - 1, 1, x1 - 1, i});
event.push_back({y2, 2, x1 - 1, i});
event.push_back({y1 - 1, 2, x2, i});
}
sort(event.begin(), event.end());
sort(vx.begin(), vx.end());
vx.erase(unique(vx.begin(), vx.end()), vx.end());
m = vx.size();
for(auto evt : event) {
if(evt[1] == 0) {
int y = lower_bound(vx.begin(), vx.end(), evt[2]) - vx.begin() + 1;
b.update(y);
} else {
int y = upper_bound(vx.begin(), vx.end(), evt[2]) - vx.begin();
int tmp = b.Query(y);
if(evt[1] == 1) ans[evt[3]] += tmp;
else ans[evt[3]] -= tmp;
}
}
for(int i = 1; i <= q; ++i) printf("%d\n", ans[i]);
return 0;
}
相关问题
1. 区间不同数之和
我们定义 \(pre_i\) 表示 \(a_i\) 这个数上一次出现的位置,如果没有就是 \(0\)。那么我们考虑一个询问 \([l,r]\) 之间的东西对于答案的贡献是什么,这个位置 \(i\) 如果有贡献,那么就必须得 \(pre_i < l\) 那么这个数才会有贡献,所以我们现在要加和满足 \(\begin{cases}pre_i < l\\ l \leq i \leq r\end{cases}\) 的个数,这就是一个普通的二维数点问题。只不过我们在另一位上只需要把它拆成两个部分了,一个部分就是 \(i \leq l-1\) 的,一部分是 \(i \leq r\) 的。
我们就建一个点 \((i, pre_i)\) 然后对 \(i\) 这一维离散化,对于 \(pre_i\) 这一位排序建立事件。
虽然写的时候非常奇怪但是还是 A 了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
template <typename T>inline void read(T& t){t=0; register char ch=getchar(); register int fflag=1;while(!('0'<=ch&&ch<='9')) {if(ch=='-') fflag=-1;ch=getchar();}while(('0'<=ch&&ch<='9')){t=t*10+ch-'0'; ch=getchar();} t*=fflag;}
template <typename T,typename... Args> inline void read(T& t, Args&... args) {read(t);read(args...);}
const int N = 5e5 + 10, inf = 0x3f3f3f3f;
int n, q, pre[N], nxt[N], a[N];
long long ans[N];
struct BIT {
int a[N];
void update(int u, int va) {for(; u <= n; u += u & (-u)) a[u] += va;}
long long Query(int u) {
long long res = 0;
for(; u; u -= u & (-u)) res += a[u];
return res;
}
}b;
vector<array<int,4> >event;
vector<int>vx;
int main() {
read(n, q);
for(int i = 1; i <= n; ++i) {
read(a[i]);
pre[i] = nxt[a[i]];
nxt[a[i]] = i;
//cout << i << ' ' << pre[i] << endl;
event.push_back({pre[i], 0, i});
}
for(int i = 1; i <= q; ++i) {
int l, r;
read(l, r);
event.push_back({l - 1, -1, l - 1, i});
event.push_back({l - 1, 1, r, i});
}
sort(event.begin(), event.end());
for(auto evt : event) {
//cout << evt[0] << ' ' << evt[1] << ' ' << evt[2] << ' ' << evt[3] << endl;
if(evt[1] == 0) b.update(evt[2], a[evt[2]]);
else {
ans[evt[3]] += evt[1] * b.Query(evt[2]);
}
}
for(int i = 1; i <= q; ++i) printf("%lld\n", ans[i]);
return 0;
}
/*
是谁挥霍的时光啊,是谁苦苦的奢望啊
这不是一个问题,也不需要你的回答
No answer.
*/
2.区间 lower_bound
我们把每个点看做 \((i,a_i)\),我们就是要统计 \(x\) 轴在 \([l,r]\) 范围内的 \(y\) 轴在 \(x\) 上面的点的最下面的一个点,这个事情扫描线一下就完事儿了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
template <typename T>inline void read(T& t){t=0; register char ch=getchar(); register int fflag=1;while(!('0'<=ch&&ch<='9')) {if(ch=='-') fflag=-1;ch=getchar();}while(('0'<=ch&&ch<='9')){t=t*10+ch-'0'; ch=getchar();} t*=fflag;}
template <typename T,typename... Args> inline void read(T& t, Args&... args) {read(t);read(args...);}
const int N = 2e5 + 10, inf = 0x3f3f3f3f;
int n, q, a[N];
vector<array<int, 5> >event;
struct Segment_Tree {
int minn[N << 2], lc[N << 2], rc[N << 2];
void pushup(int u) {minn[u] = min(minn[u << 1], minn[u << 1 | 1]);}
void build(int u, int l, int r) {
lc[u] = l, rc[u] = r;
if(l == r) {
minn[u] = inf;
return;
}
build(u << 1, l, l + r >> 1), build(u << 1 | 1, (l + r >> 1) + 1, r);
pushup(u);
}
int Query(int u, int l, int r) {
if(l <= lc[u] && r >= rc[u]) return minn[u];
if(l > rc[u] || lc[u] > r) return inf;
return min(Query(u << 1, l, r), Query(u << 1 | 1, l, r));
}
void update(int u, int p, int va) {
if(lc[u] == rc[u]) {
minn[u] = va;
return;
}
if(p <= (lc[u] + rc[u] >> 1)) update(u << 1, p, va);
else update(u << 1 | 1, p, va);
pushup(u);
}
}seg;
int ans[N];
int main() {
read(n, q);
for(int i = 1; i <= n; ++i) {
read(a[i]);
event.push_back({-a[i], 0, i});
}
for(int i = 1; i <= q; ++i) {
int l, r, x;
read(l, r, x);
event.push_back({-x, 1, l, r, i});
}
seg.build(1, 1, n);
sort(event.begin(), event.end());
for(auto evt : event) {
if(evt[1] == 0) seg.update(1, evt[2], -evt[0]);
else {
int res = seg.Query(1, evt[2], evt[3]);
if(res >= inf) res = -1;
ans[evt[4]] = res;
}
}
for(int i = 1; i <= q; ++i) printf("%d\n", ans[i]);
return 0;
}
/*
是谁挥霍的时光啊,是谁苦苦的奢望啊
这不是一个问题,也不需要你的回答
No answer.
*/


