[树形dp]CCPC Qinhuangdao 2020 K, Kingdom's Power做题思路

首先，对于一个子树，我们显然只有两种去让军队走过他的办法，一种是从兄弟节点调一些军队来，另一种是从根节点推过来。

感觉有一个结论，就是我这个位置如果用兄弟节点推过来的只是因为兄弟节点推过来的步数小于从根节点重新来一个步数小。

我们首先会遇到一个问题，如果现在兄弟节点推过来的确实比从根来小，但是有没有可能这个给其他兄弟节点更优一点呢？这是不可能的。

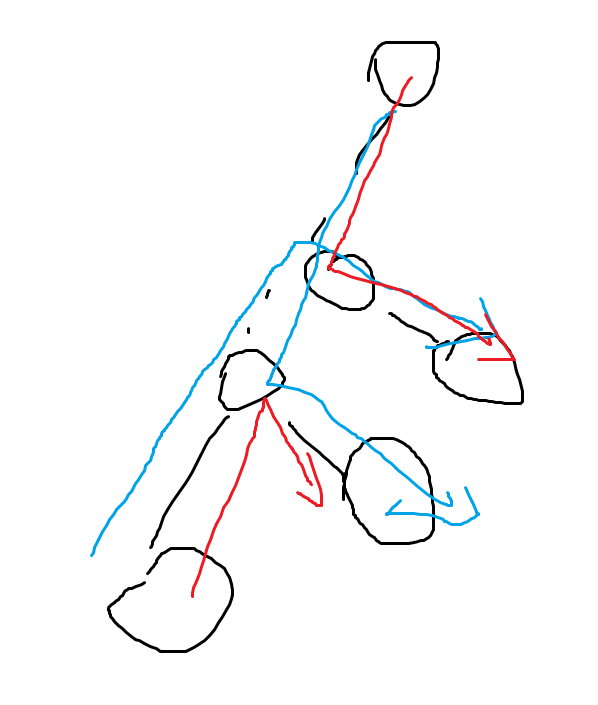
蓝色的线与红色的线都是选择，会发现他们所需要的步数其实是一样的。

还有一件事情，我们如果最优的情况下面有多个路线上来，这是肯定不优滴。

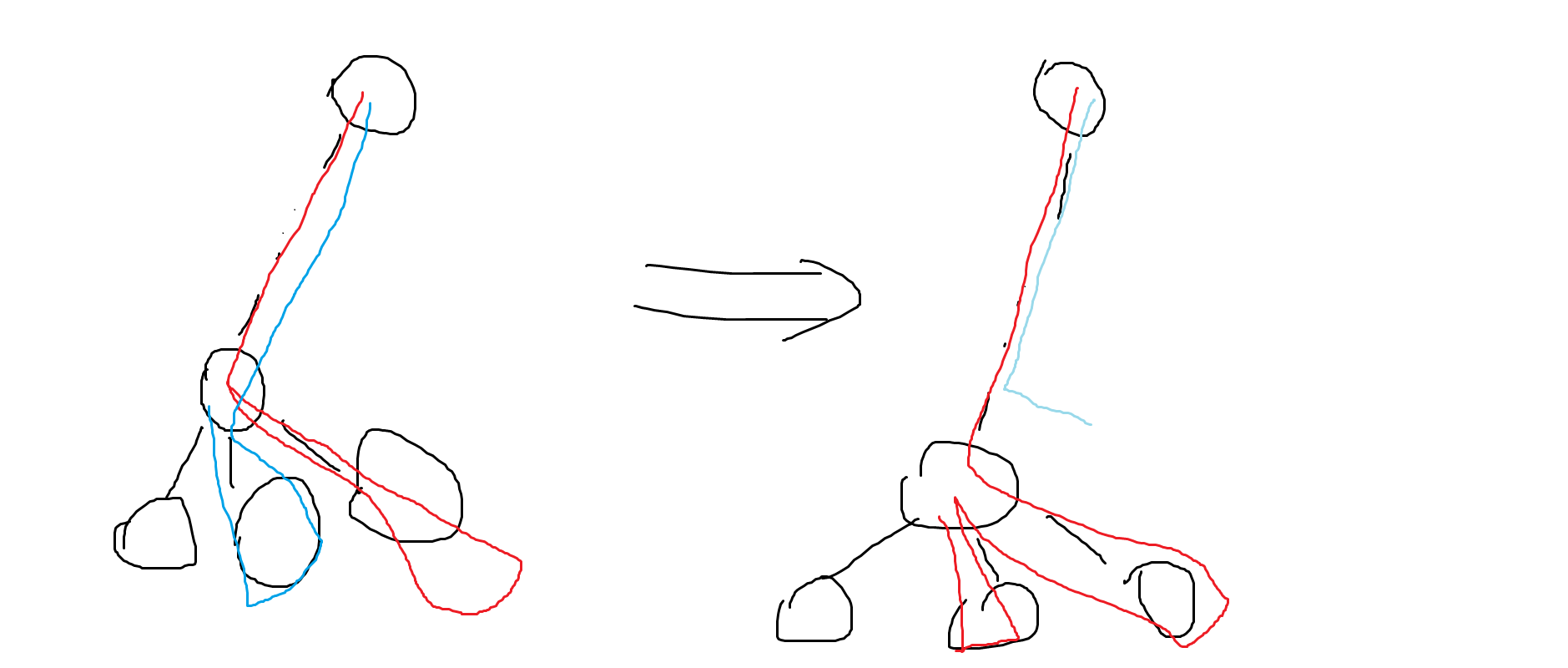
同时，我们可以想到的一点是，我们应该按照节点的深度来排序操作，因为每个军队如果停下来的话他肯定停在叶子节点。从小到大的排序每个节点。

想法是对的，但是代码实现过于 ex 直接抄的

// *2022/08/30 19:03:38 created
// *By : Foofish
// *At : QHSMS
#include <bits/stdc++.h>
using namespace std;
template <typename T>inline void read(T& t){t=0; register char ch=getchar(); register int fflag=1;while(!('0'<=ch&&ch<='9')){if(ch=='-') fflag=-1;ch=getchar();}while(('0'<=ch&&ch<='9')){t=t*10+ch-'0'; ch=getchar();} t*=fflag;}
template <typename T,typename... Args> inline void read(T& t, Args&... args){read(t);read(args...);}
const int N=1e6+10;
typedef pair<int,int>PII;
int T,n,fa[N],dep[N],dp[N],val[N],cnt[N];
vector<PII>G[N];
int dfs(int u,int val){
    if(G[u].empty()) return 1;
    dep[u]=val;
    for(pair<int,int> &it:G[u]) if(it.second!=fa[u]) it.first=max(it.first+1,dfs(it.second,val+1));
    sort(G[u].begin(),G[u].end());
    return G[u].back().first+1;
}
int dfs1(int u,int val){
    //我们在过程中维护一个参数 val 表示现在的兄弟节点的有兵在的叶节点的走到 u 所需要的最小值.
    cnt[u]=val;
    if(G[u].empty()) return 1;
    int p=val;
    for(pair<int,int> it:G[u]) p=min(dep[u],dfs1(it.second,p+1));
    return p+1;
}
void write(int x){
    if(x>=10) write(x/10);
    putchar(x%10+'0');
}
int main(){
    read(T);
    int tot=0;
    while(T--){
        read(n);
        for(int i=1;i<=n;++i) G[i].clear(),dp[i]=dep[i]=cnt[i]=val[i]=0;
        for(int i=2;i<=n;++i){
            read(fa[i]);
            G[fa[i]].push_back(make_pair(0,i));
            dp[i]=dp[fa[i]]+1;
        }
        dfs(1,0);
        dfs1(1,0);
        int ans=0;
        for(int i=1;i<=n;++i)
           if(G[i].empty()) ans+=cnt[i];
        putchar('C');
        putchar('a');
        putchar('s');
        putchar('e');
        putchar(' ');
        putchar('#');
        write(++tot);
        putchar(':');
        putchar(' ');
        write(ans);
        putchar('\n');
    }
    return 0;
}