快速傅里叶变换(FFT)——从入门到入土
FFT (快速傅里叶变换)——从入门到入土
请不要转载，谢谢。版权于江苏省前黄高级中学 刘成宇 手中
前置知识
多项式系数/点值表达法
对于一个多项式 \(A(x)=\sum\limits_{i=0}^{n-1}{a_i*x^i}\)
明显是一个 \(n-1\) 次函数/多项式，给这种对于 对应关系 \(A\) 的种类一个名称——多项式的系数表达法。
还有什么表示方式呢？下面给出一条引理
用 \(n+1\) 个点可以确定一条 \(n\) 次函数图像。
感性证明：
\(\begin{cases}y_1=a_0+a_1*x_1+...+a_{n-1}*x_1^{n-1} \\ y_2=a_0+a_1*x_2+...+a_{n-1}*x_2^{n-1} \\ y_3=a_0+a_1*x_3+...+a_{n-1}*x_3^{n-1} \\ ...\end{cases}\)
这时候注意到，如果我现在 \(x_1 \not= x_2 \not= x_3 ... \not= x_n+1\) 那么我是不是用加减消元法最终可以确定 \(a_0,a_1,a_2,...,a_{n-1}\)
那么这时候就简单了，可以用点刻画函数。即为点值表示法。用形如 \(A(x)=\{(x_1,y_1),(x_2,y_2),...,(x_{n},y_{n})\}\) 表示
复数计算
如果两个复数相乘 \((a+bi)*(c+di)=ac-bd+(bc+ad)i\)
如果两个复数相加或相减比较简单，这里就不给出了。
复平面
本文令 \(i = \sqrt{-1}\)
快速傅里叶变换是基于复数的，复平面是其中一个基本的知识。
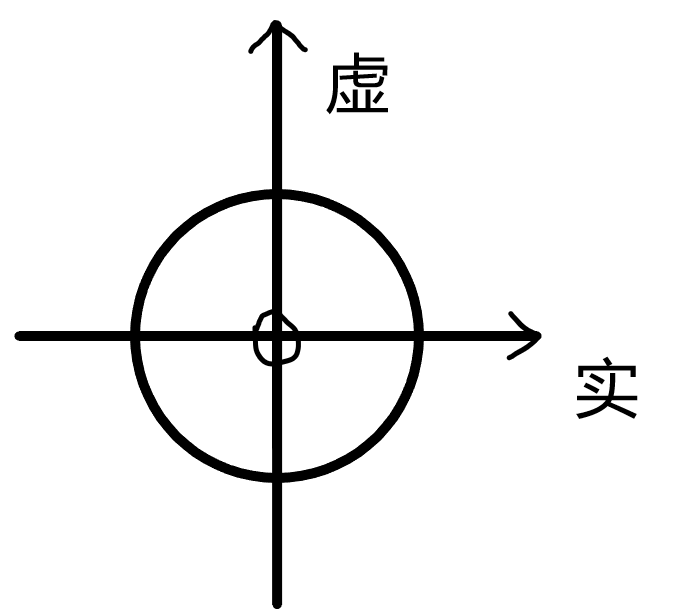
注意，原点是不在虚轴上的，因为 \(0i=0\) 而 \(0\) 是实数
就类似于上面这样一个平面。对于平面上任意一个点 \((a,b)\) 其都表示一个复数 \(a+bi\) 。
如果我现在要对复平面上的一个点 \((a,b)\) 平方。
因为在单位圆上 所以有 \(|(a,b)|=\sqrt{a^2+b^2}=1\) 即 \(a^2+b^2=1\)
首先计算它的值 \((a+bi)^2=a^2-b^2+2abi\)
新的点 \((a^2-b^2,2ab)\) 计算一下模长
\(|(a^2-b^2,2ab)|=\sqrt{(a^2-b^2)^2+4a^2b^2}=\sqrt{a^4+b^4-2a^2b^2+4a^2b^2}=\sqrt{a^4+b^4+2a^2b^2}=\sqrt{(a^2+b^2)^2}=1\)
所以，现在的这个点仍然在单位圆上。
接下来考虑一下它与原点连线后的旋转角 \(\theta_2\) 与原旋转角 \(\theta_1\) 的关系。
由于原来的点坐标是 \((a,b)\) 所以有 \(\tan{\theta_1}=\frac{b}{a}\) 不妨令 \(\frac{b}{a}=\lambda\)
那么综合现在的坐标就有 \(\tan{\theta_2}=\frac{2ab}{a^2-b^2}\) 类似于 whk 中处理的套路，齐次式将上边的除下去。
\(\tan{\theta_2}=\frac{2}{\frac{a}{b}-\frac{b}{a}}=\frac{2\lambda}{1-\lambda^2}\) 不难看出二倍角公式，那么有
\(\theta_2=2\theta_1\) 就相当于多转了一个 \(\theta_1\) 这种特殊性就是 FFT 为什么所撷取的。
真正的FFT
FFT 正变换
快速傅里叶变换，处理多项式乘法时非常有用。既然是多项式乘法，那不可能是用一般的系数表达式一个一个乘，那么得想一个更好的办法，由于:
对于点值表达法计算 \(A(i)\times B(i)\) 答案 \(C(i)=\{(x_0,A_{x0}B_{x0}),(x_1,A_{x1}B_{x1}),(x_2,A_{x2}B_{x2}),...,(x_n,A_nB_n)\}\)
明显发现对于点值表达法计算乘法只需要 \(\mathbf{O}(n)\) 如此优秀的时间就 ok 了，那么直接使用点值表达法就 ok 啦。这时候遇到的最大的一个问题就是，对于直观的系数表达法与抽象但好用的点值表达法之间，我如何去转化，这一点是值得我们去思考的。这也是 FFT 区别于或者说优于 DFT 的一个特点。
现在就是要计算 \(n\) 个 \(A(x)\) 且这些 \(x\) 互不相同，总时间复杂度还不能有 \(\mathbf{O}(n^2)\) 怎么办。
先把 \(n\) 转化成一个大于 \(n\) 二的整数次幂的形式，不够的高位上系数补 \(0\) ，然后进行操作。
复数就派上用场了，选取的就是 \(\omega^k_n\quad \forall k\in[0,n)\) 这个时候因为这里的 \(n\) 肯定是大于原来的 \(n\) 的，所以即使取 \(n\) 个点也是可以计算出原来的值的。
现在就是要计算 \(A(\omega^k_n)\) 了。
首先，稍微的将 \(A(x)=\sum\limits_{i=0}^{n-1}{a_i*x^i}\) 展开看看 \(A(x)=a_0+a_1*x+a_2*x^2+...+a_{n-1}x^{n-1}\) 这时候做这样一步构造
令 \(A_1(x)=a_0+a_2*x+a_4*x^2+...+a_{n-2}*x^{\frac{n}{2}-1}\)
\(A_2(x)=a_1+a_3*x+a_5*x^2+...+a_{n-1}*x^{\frac{n}{2}-1}\)
显然有 \(A(x)=A_1(x^2)+x*A_2(x^2)\)
将 \(A(\omega^k_n)\) 写出来看看
\(A(\omega^k_n)=A_1(\omega^{2k}_n)+\omega^k_n*A_2(\omega^{2k}_n)=A_1(\omega^k_{\frac{n}{2}})+\omega^k_n*A_2(\omega^k_{\frac{n}{2}})\)
好的，但是问题并没有解决，即使化成这种形式，还是找不到任何优化的点。这时候分类讨论一波
- 如果当 \(0\leq k<\frac{n}{2}\) 时，我就用\(A(\omega^k_n)=A_1(\omega^k_{\frac{n}{2}})+\omega^k_n*A_2(\omega^k_{\frac{n}{2}})\)算就 ok 了。
- 如果当 \(n>k\ge\frac{n}{2}\) 时，不妨令 \(t=k+\frac{n}{2}\) 那么这个 \(t\) 又回到了上一个情况了，就有 \(A(k)=A_1(\omega^{2k+n}_n)+\omega^{k+\frac{n}{2}}_n*A_2(\omega^{2k+n}_n)\)
首先 \(\omega^{2k+n}_n=\omega^{2k}_n*\omega^n_n=\omega^{2k}_n\)
并且 \(\omega^{k+\frac{n}{2}}_n=-\omega^{k}_n\)
那么就有 \(A(k)=A_1(\omega^{2k}_n)-\omega^{k}_n*A_2(\omega^{2k}_n)=A_1(\omega^k_{\frac{n}{2}})-\omega^k_n*A_2(\omega^k_{\frac{n}{2}})\)
连起来
\(A(\omega^k_n)=A_1(\omega^k_{\frac{n}{2}})+\omega^k_n*A_2(\omega^k_{\frac{n}{2}})\qquad k\in[0,\frac{n}{2})\)
\(A(\omega^{k+\frac{n}{2}}_n)=A_1(\omega^k_{\frac{n}{2}})-\omega^k_n*A_2(\omega^k_{\frac{n}{2}})\qquad k\in[\frac{n}{2},n)\)
发现了特殊的地方，两个的差距只有一个 \(\omega^k_n*A_2(\omega^k_{\frac{n}{2}})\) ,那么就其实我们可以通过计算 \(A_1(\omega^k_{\frac{n}{2}})\) 以及 \(A_2(\omega^k_{\frac{n}{2}})*\omega^k_n\) 就能求出 \(A(\omega^k_n)\) 以及 \(A(\omega^{k+\frac{n}{2}}_n)\)
那么求 \(A(1),A(2),...,A(n)\) 就被切成了一半，只需要求一半就 ok 了。
这个时候观察一下所要求的 \(A_1(x),A_2(x)\) 也是一个可以使用这种方法的式子，那么使用这种同样的方法就可以了。
有点像线段树分治一样。
FFT 负变换
上面的正变换只是一半，是把这个东西转化成点值表达法的方式，由于 正常 的题目最后肯定还是要你转化成系数表达式的，那么还需还需要进行将点值表达式转化为系数表达式。
怎么操作呢，确实很难，但是总有大佬能想到。是一种构造法。
令 \(f(x)= \sum\limits_{i=0}^{n}y_i*x^i\) 其中 \(y_i\) 就是上面的点值表达式中的所有纵坐标
先给出结论把
\(a_k=\frac{f(\omega_n^{-k}\ )}{n}\)
证明一波：
\(f(\omega_n^{-k})=\sum\limits_{i=0}^{n}y_i*\omega_n^{-ik}\)
由于 \(y_i=\sum\limits_{j=0}^{n}\omega_n^{ij}*a_j\)
代入
\(f(\omega_n^{-k})=\sum\limits_{i=0}^{n}[\sum\limits_{j=0}^{n}\omega_n^{ij}*a_j]*\omega_n^{-ik}\)
像莫比乌斯反演一样套路调换顺序
\(f(\omega_n^{-k})=\sum\limits_{j=0}^{n}\sum\limits_{i=0}^{n}[\omega_n^{ij}*a_j]*\omega_n^{-ik}\)
整理整理
\(f(\omega_n^{-k})=\sum\limits_{j=0}^{n}a_j\sum\limits_{i=0}^{n}(\omega_n^{j-k})^i\)
这时候思考一下后面的东西
令 \(S(x)=1+x+x^2+...+x^{n-1}\)
\(xS(x)=x+x^2+x^3+...+x^n\)
两式相减 \((x-1)S(x)=x^n-1\)
\(S(x)=\frac{x^n\ -1}{x-1}\)
将 \(x=\omega_n^u\) 代入
\(\\S(\omega_n^u)=\frac{(\omega_n^n)^u-1}{\omega_n^u-1}=\frac{1-1}{\omega_n^u-1}\\\)
显然，上式为 \(0\) ,但是，除非 \(\omega_n^u-1 = 0\) 即分母为 \(0\) 时，思考一下什么意思就是 \(n=u\) 时呗。根据定义，此时 \(S(\omega_n^u)=n\)
好的，处理了这些，将 \(S(x)\) 代回去
\(f(\omega_n^{-k})=\sum\limits_{j=0}^{n}a_j\sum\limits_{i=0}^{n}(\omega_n^{j-k})^i\)
发现当且仅当 \(j=k\) 时原式才有值。 \(f(\omega_n^{-k})=a_k*n\)
证到这里，两边再除以 \(n\) ，答案就出来了。
当然，为了求值，再回眸看一眼这个 \(f(\omega_n^{-k})\) 有无何特殊的地方，这不就是刚才算的正变换把 \(\omega_n^{k}\) 换成了 \(\omega_n^{-k}\) 么？
所以，正变换和逆变换是两个相反的运算，从某种方面理解，就是多转了半圈。
FFT 递归版 die 码
#include <bits/stdc++.h>
#define debug puts("I ak IOI several times");
#define pb push_back
using namespace std;
template <typename T>inline void read(T& t){
t=0; register char ch=getchar(); register int fflag=1;
while(!('0'<=ch&&ch<='9')){if(ch=='-') fflag=-1;ch=getchar();}
while(('0'<=ch&&ch<='9')){t=((t<<1)+(t<<3))+ch-'0'; ch=getchar();} t*=fflag;
}
template <typename T,typename... Args> inline void read(T& t, Args&... args){
read(t);read(args...);
}
template <typename T>inline void write(T x){
if(x<0) putchar('-'),x=~(x-1); int s[40],top=0;
while(x) s[++top]=x%10,x/=10; if(!top) s[++top]=0;
while(top) putchar(s[top--]+'0');
}
const double PI=acos(-1.0);
const int MAXN=2500005;
struct Complex{
double x,y;
Complex(double _x=0,double _y=0){x=_x,y=_y;}
}a[MAXN],b[MAXN],c[MAXN];
Complex operator + (Complex a,Complex b){return Complex(a.x+b.x,a.y+b.y);}
Complex operator - (Complex a,Complex b){return Complex(a.x-b.x,a.y-b.y);}
Complex operator * (Complex a,Complex b){return Complex(a.x*b.x-a.y*b.y,a.y*b.x+a.x*b.y);}
void FFT(Complex *y,int len,int type){
if(len<=1) return;
int mid=len>>1;
Complex a1[mid],a2[mid];
for(int i=0;i<mid;++i) a1[i]=y[i<<1],a2[i]=y[i<<1|1];
FFT(a1,mid,type);FFT(a2,mid,type);
Complex Wn=Complex(cos(2*PI/len),type*sin(2*PI/len)),w(1,0);
for(int i=0;i<mid;++i){
Complex wt=w*a2[i];
y[i]=a1[i]+wt;
y[i+mid]=a1[i]-wt;
w=w*Wn;
}
}
int n,m,limit;
int main(){
read(n,m);
for(int i=0;i<=n;++i) cin>>a[i].x;
for(int i=0;i<=m;++i) cin>>b[i].x;
limit=1;while(limit<=n+m) limit<<=1;
FFT(a,limit,1); FFT(b,limit,1);
for(int i=0;i<=limit;++i) c[i]=a[i]*b[i];
FFT(c,limit,-1);
for(int i=0;i<=n+m;++i) cout<<(int)(c[i].x/limit+0.5)<<' ';
return 0;
}
//Welcome back,Chtholly.
递推优化 FFT
蝴蝶操作
观察到在原来的操作中有这样一步。
Complex wt=w*a2[i];
y[i]=a1[i]+wt;
y[i+mid]=a1[i]-wt;
w=w*Wn;
现在称其为蝴蝶操作
类似于下图
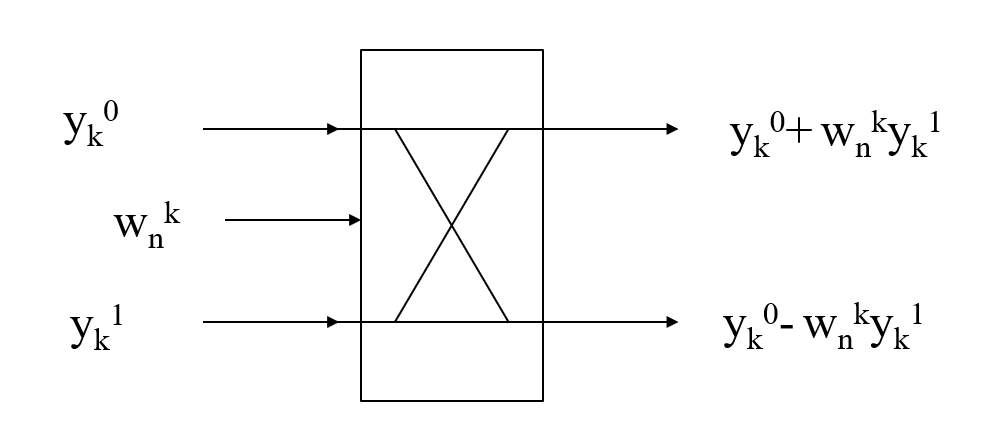
发现规律
对于原来的递归版 FFT ，不难发现，很多一大部分是将数组拆分的过程，那这个数组拆分的有没有规律呢？
还真有，这里继续引用一下谷里的题解图片。
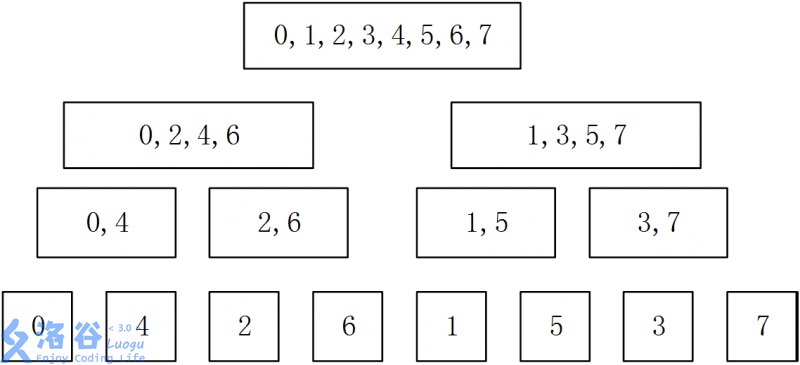
这时候把最后一行全部转成二进制：
\(000,100,010,110,001,101,011,111\)
reverse一下
\(000,001,010,011,100,101,110,111\)
转成十进制发现就是 \(0,1,2,3,4,5,6,7\) 那么这个规律好用了呀。
只需要提前构造一下数组就 ok 了，将数组变成 \(0,4,2,6,1,5,3,7\) 的模样似乎就不用拆分了？ 是的。
这里想一下如何 reserve 。
令 \(i\) 号反转成 \(rev_i\) 。
如果我正着做，显然 \(rev_{\left\lfloor\frac{i}{2}\right\rfloor}\) 时已经处理好了的。
想想 \(rev_{\left\lfloor\frac{i}{2}\right\rfloor}\) 和 \(rev_i\) 有没有什么关系。
\(\left\lfloor\frac{i}{2}\right\rfloor\) 不就是 \(i\) 右移一位嘛，那么它如果全部反转的话应该在第一位。好了，那么只需要看原来的 \(i\&1\) 是不是 \(1\) 就行了，是 \(1\) 把开头一位换成 \(1\) .
for(int i=0;i<limit;++i) rev[i]=(rev[i>>1]>>1)|((i&1)*(1<<L-1));
die 码一行，简洁易懂常数小
迭代 FFT
知道了这些，迭代 FFT 只不过是一步之遥。只需要想想 die 码的细节就好了，这里给出一张宝贵的图。
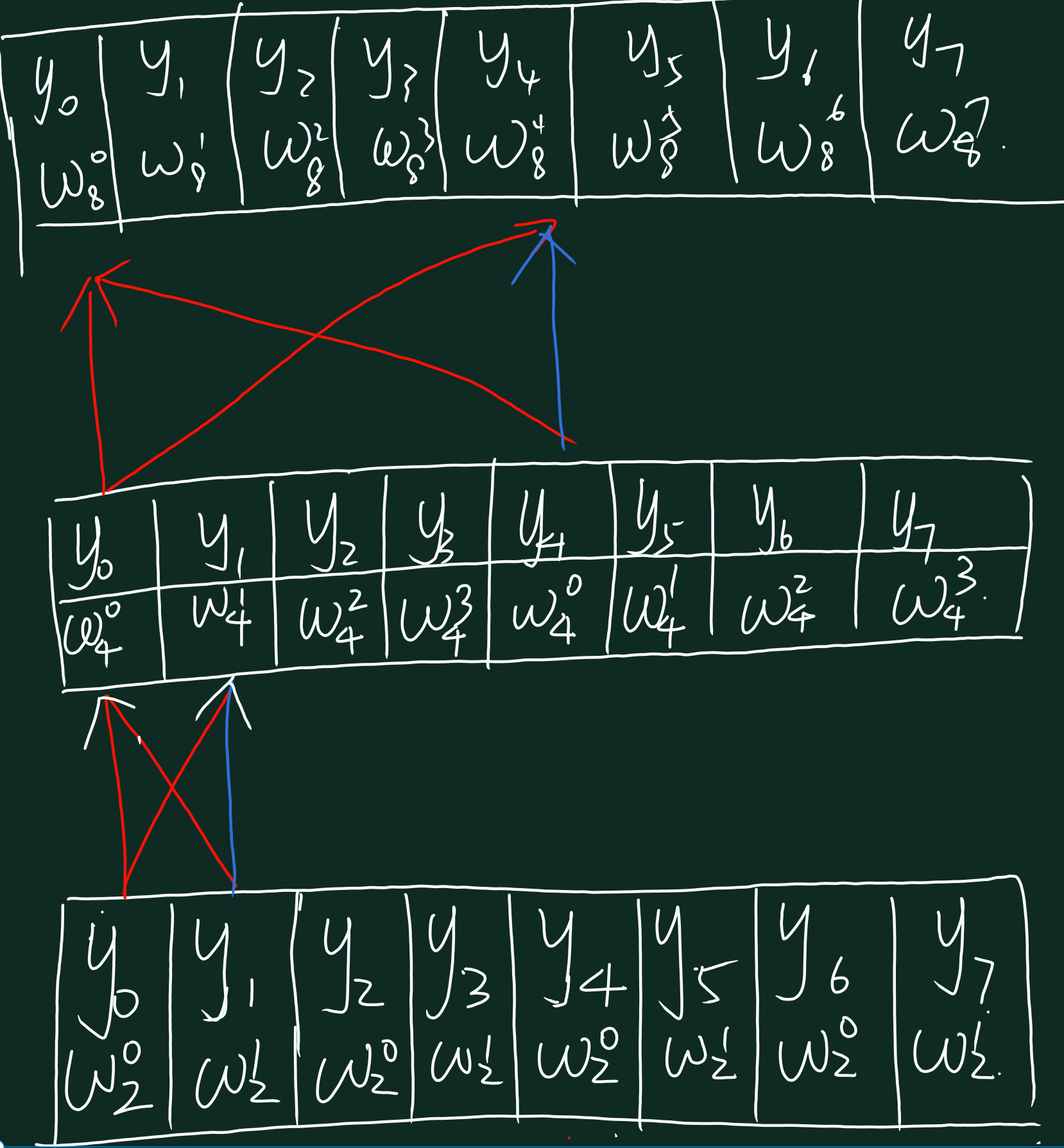
我感觉这张图已经非常好理解力。
下面上 die 码：
#include <bits/stdc++.h>
#define debug puts("I ak IOI several times");
#define pb push_back
using namespace std;
template <typename T>inline void read(T& t){
t=0; register char ch=getchar(); register int fflag=1;
while(!('0'<=ch&&ch<='9')){if(ch=='-') fflag=-1;ch=getchar();}
while(('0'<=ch&&ch<='9')){t=((t<<1)+(t<<3))+ch-'0'; ch=getchar();} t*=fflag;
}
template <typename T,typename... Args> inline void read(T& t, Args&... args){
read(t);read(args...);
}
template <typename T>inline void write(T x){
if(x<0) putchar('-'),x=~(x-1); int s[40],top=0;
while(x) s[++top]=x%10,x/=10; if(!top) s[++top]=0;
while(top) putchar(s[top--]+'0');
}
const double PI=acos(-1.0);
const int MAXN=2500005;
struct Complex{
double x,y;
Complex(double _x=0,double _y=0){x=_x,y=_y;}
}a[MAXN],b[MAXN],c[MAXN];
Complex operator + (Complex a,Complex b){return Complex(a.x+b.x,a.y+b.y);}
Complex operator - (Complex a,Complex b){return Complex(a.x-b.x,a.y-b.y);}
Complex operator * (Complex a,Complex b){return Complex(a.x*b.x-a.y*b.y,a.y*b.x+a.x*b.y);}
int rev[MAXN],limit,L,n,m;
void FFT(Complex *y,int type){
for(int i=0;i<limit;++i) if(rev[i]>i) swap(y[i],y[rev[i]]);
for(int len=2;len<=limit;len<<=1){
Complex Wn(cos(2*PI/len),type*sin(2*PI/len));
int mid=len>>1;
for(int L=0,R=len-1;R<=limit;L+=len,R+=len){
Complex w(1,0);
for(int p=L;p<L+mid;++p){
Complex X=y[p]+w*y[p+mid],Y=y[p]-w*y[p+mid];
y[p]=X;y[p+mid]=Y;
w=w*Wn;
}
}
}
}
int main(){
read(n,m);
for(int i=0;i<=n;++i) cin>>a[i].x;
for(int i=0;i<=m;++i) cin>>b[i].x;
limit=1;while(limit<=n+m) limit<<=1,++L;
for(int i=0;i<limit;++i) rev[i]=(rev[i>>1]>>1)|((i&1)*(1<<L-1));
FFT(a,1);FFT(b,1);
for(int i=0;i<=limit;++i) c[i]=a[i]*b[i];
FFT(c,-1);
for(int i=0;i<=n+m;++i) cout<<(int)(c[i].x/limit+0.5)<<' ';
return 0;
}
//Welcome back,Chtholly.
