[floyd]题解 洛谷P1119 灾后重建

作为一道 Floyd 的妙题，其非常重要。

首先，我们重新审视一下我们之前对于 背诵 的 Floyd 的板子。（如果之前就已经非常了解 Floyd ，完全可以跳过。）

for(int k=1;k<=n;++k)
	for(int i=1;i<=n;++i){
		if(k==i) continue;
		for(int j=1;j<=n;++j){
			if(k==j||i==j) continue;
			if(f[i][j]>f[i][k]+f[k][j]) f[i][j]=f[i][k]+f[k][j];
		}
	}

那么每次对于 \(k\) 的循环，算的其实是只用前 \(k-1\) 个节点中转图上的最短路。

正确性就在于，如果我现在对前 \(k-1\) 个节点已经作为中转过了，那么对于下面这张图。

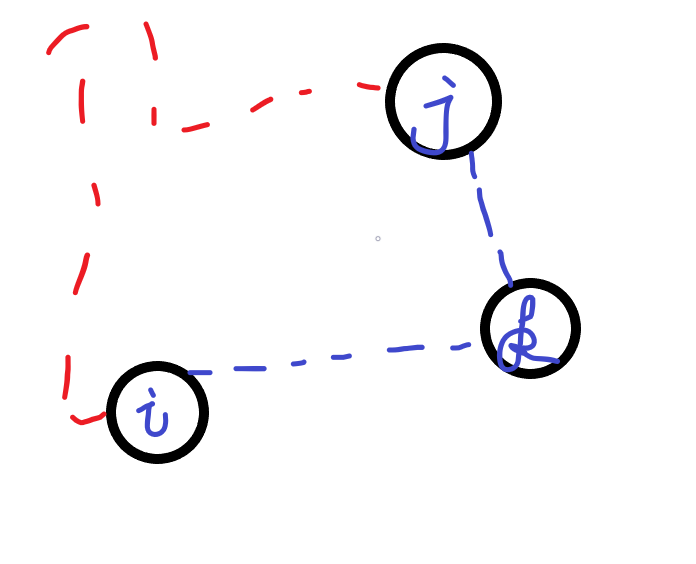
即为 \(i\) 到 \(j\) 可以通过 \(k\) 等等点来中转，进一步获取新的最短路。因为之前的一定正确，那么就是说，我现在从 \(i\) 到 \(k\) 的 目前的 最短路已经确定，从 \(k\) 到 \(j\) 的 目前的 最短路也已经确定。

为什么已经确定了呢？ 就是因为我之前的点已经松弛过了，那么 \(i\) 和 \(k\) 之间不可能通过一条 \((l,k) \qquad l\in[1,k)\) 使之更短。

这就是 Floyd 的正确性。

这也启示要深刻理解每个算法的深层。刨根问底。

---

对于此题。

好了，已经知道 \(k\) 这个循环是对于前 \(k\) 个节点的最短路了，那么对于每组询问，我只需要把已经修好了的前 \(k\) 个循环一遍就 ok 了。

时间复杂度最坏也为 \(\mathbf{O}(n^3)\)
写代码只需注意一下这题点从 \(0\) 开始就 ok 了。

#include <bits/stdc++.h>
#define debug puts("I ak IOI several times");
#define pb push_back
using namespace std;
template <typename T>inline void read(T& t){
    t=0; register char ch=getchar(); register int fflag=1;
    while(!('0'<=ch&&ch<='9')){if(ch=='-') fflag=-1;ch=getchar();}
    while(('0'<=ch&&ch<='9')){t=((t<<1)+(t<<3))+ch-'0'; ch=getchar();} t*=fflag;
}
template <typename T,typename... Args> inline void read(T& t, Args&... args){
    read(t);read(args...);
}
template <typename T>inline void write(T x){
    if(x<0) putchar('-'),x=~(x-1); int s[40],top=0;
    while(x) s[++top]=x%10,x/=10; if(!top) s[++top]=0;
    while(top) putchar(s[top--]+'0');
}
const int MAXN=205,MAXM=50005;
int dp[MAXN][MAXN],n,m,t[MAXN],Q,a[MAXN][MAXN],k;
void update(){
	//前 k 个点的松弛操作 
	for(int i=0;i<n;++i)
		for(int j=0;j<n;++j)
			if(dp[i][j]>dp[i][k]+dp[k][j])
				dp[i][j]=dp[j][i]=dp[i][k]+dp[k][j];
}
int main(){
	read(n,m);
	memset(dp,0x3f,sizeof(dp));
	for(int i=0;i<n;++i) read(t[i]),dp[i][i]=0;
	dp[0][0]=0;
	while(m--){
		int x,y,val;
		read(x,y,val);
		dp[x][y]=dp[y][x]=val;
	}
	read(Q);
	while(Q--){
		int x,y,tim;
		read(x,y,tim);
		while(tim>=t[k]&&k<n){
			update();
			++k;
		}
		if(tim<t[x]||tim<t[y]) cout<<-1<<endl;
		else if(dp[x][y]==0x3f3f3f3f) cout<<-1<<endl;
		else cout<<dp[x][y]<<endl;
	}
    return 0;
}
//Welcome back,Chtholly.