[分层图]P1073 [NOIP2009 提高组] 最优贸易 题解

作为一道被蒟蒻纳入 trick 的题，很多是借鉴了洛谷中题解的。但是还是在这里写下来，让以后的自己记住。

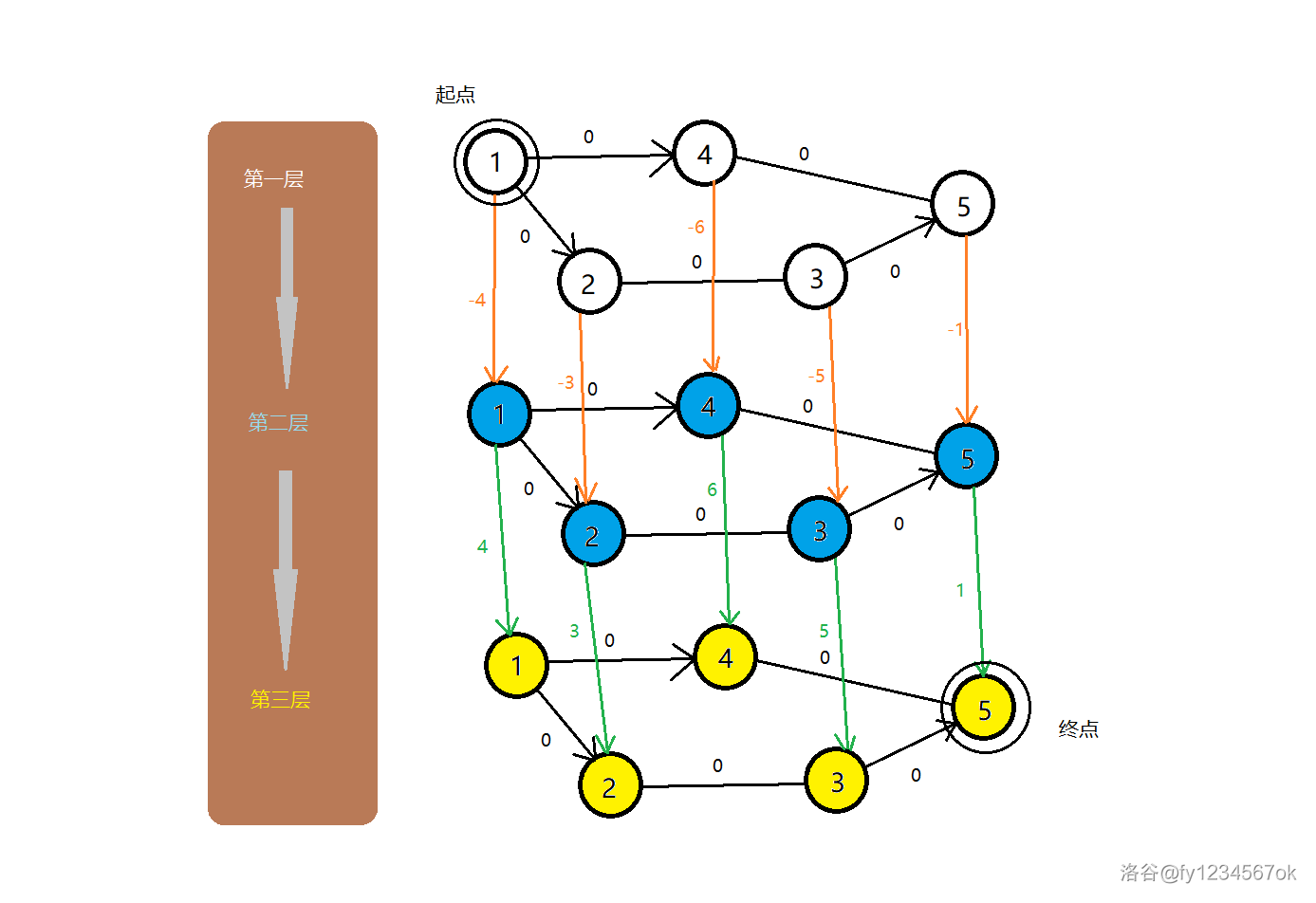
发现这道题，对于每个节点竟然有两种操作，一个卖出，一个买入，而且在所有节点都可以操作，那么分层图！这样的话，会发现卖出的状态是一个节点，买入的状态也是一个节点。

这里用一下洛谷题解的图，会发现白色的节点就是没有操作的节点，而蓝色的节点则表示买入了水晶球的节点，黄色的则是卖出了的节点。

这是样例的图。

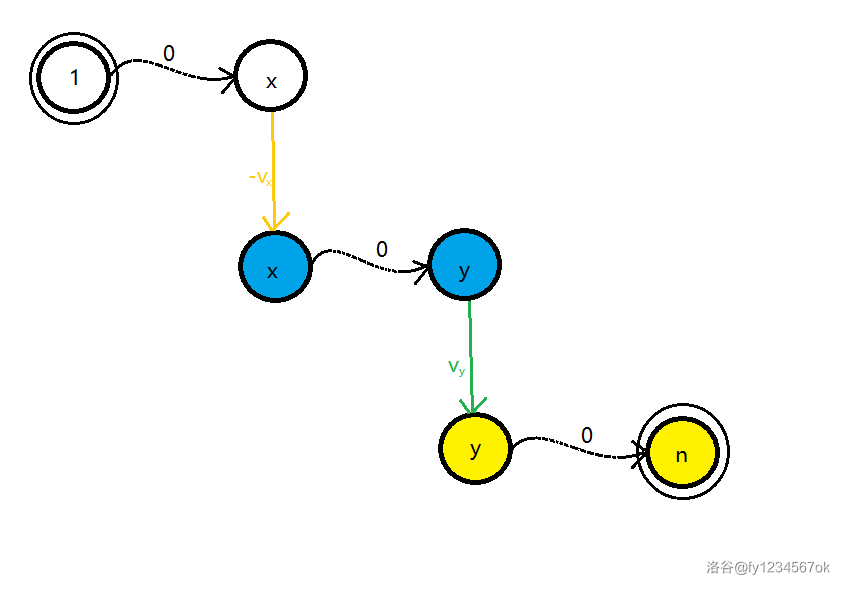
从图中也不难发现，如果我现在卖出了，在第二层图仍可以到其他节点进行操作，所以这就是算法的正确性。

die码：

#include <bits/stdc++.h>
#define debug puts("I ak IOI several times");
#define pb push_back
using namespace std;
template <typename T>inline void read(T& t){
    t=0; register char ch=getchar(); register int fflag=1;
    while(!('0'<=ch&&ch<='9')){if(ch=='-') fflag=-1;ch=getchar();}
    while(('0'<=ch&&ch<='9')){t=((t<<1)+(t<<3))+ch-'0'; ch=getchar();} t*=fflag;
}
template <typename T,typename... Args> inline void read(T& t, Args&... args){
    read(t);read(args...);
}
template <typename T>inline void write(T x){
    if(x<0) putchar('-'),x=~(x-1); int s[40],top=0;
    while(x) s[++top]=x%10,x/=10; if(!top) s[++top]=0;
    while(top) putchar(s[top--]+'0');
}
const int MAXN=500005,MAXM=2500005;
int n,m;
struct Edge{
	int to,val,nxt;
}e[MAXM];
int head[MAXM],cnt,cst[MAXN];
void add(int x,int y,int val){
	e[++cnt]={y,val,head[x]};
	head[x]=cnt;
	return;
}
queue<int>Q;
int dis[MAXN];
bool vis[MAXN];
int SPFA(){
	Q.push(1);
	memset(dis,-0x3f,sizeof(dis));
	dis[1]=0;
	while(!Q.empty()){
		int u=Q.front();
		for(int i=head[u];i;i=e[i].nxt){
			int v=e[i].to;
			if(dis[u]+e[i].val>dis[v]){
				dis[v]=dis[u]+e[i].val;
				if(!vis[v]){
					vis[v]=1;
					Q.push(v);
				}
			}
		}
		Q.pop(); vis[u]=0;
	}
	return dis[n*3];
}
void intt(){
	read(n,m);
	for(int i=1;i<=n;++i) read(cst[i]);
	for(int i=1;i<=m;++i){
		int x,y,opt;
		read(x,y,opt);
		add(x,y,0);add(n+x,n+y,0);add(2*n+x,2*n+y,0);
		if(opt==2) add(y,x,0),add(y+n,x+n,0),add(n*2+y,n*2+x,0);
	}
	for(int i=1;i<=n;++i) add(i,i+n,-cst[i]),add(i+n,i+n*2,cst[i]);
	return;
}
int main(){
	intt();
	cout<<SPFA()<<endl;
    return 0;
}
//Welcome back,Chtholly.