关于树形dp的专题探究
好,首先树形dp的关键的框架。
void dfs(int u,int fa){
///Do something
for(int i=0;i<a[u].size();++i){
//Do something
int v=a[u][i];
if(v==fa) continue;
//Do something
}
return;
}
这个框架真的很有用。
树形dp的主要关系就在于处理一下一个节点和他儿子所要求的东西的关系。
上来点题目试试!
树的直径(简化版)
题目描述
小Q最近学习了一些图论知识。根据课本,有如下定义。树:无回路且连通的无向图,每条边都有正整数的权值来表示其长度。如果一棵树有 \(N\) 个节点,可以证明其有且仅有 \(N-1\) 条边。 路径:一棵树上,任意两个节点之间最多有一条简单路径。我们用 \(dis(a,b)\) 表示点 \(a\) 和点\(b\) 的路径上各边长度之和。称 \(dis(a,b)\) 为 \(a,b\) 两个节点间的距离。
直径:一棵树上,最长的路径为树的直径。树的直径可能不是唯一的。
现在小Q想知道,对于给定的一棵树,其直径的长度是多少?(以及有多少条边满足所有的直径都经过该边,不需要计算,供思考 )
输入格式
第一行包含一个整数 \(N\) ,表示节点数。
接下来 \(N-1\) 行,每行三个整数 \(a, b, c\) ,表示点 \(a\) 和点 \(b\) 之间有一条长度为c的无向边。
输出格式
一行一个整数,表示直径的长度。
数据范围与提示
对于 100% 的测试数据:\(2\leq N\leq 200000\),\(\forall a,b,c \in [1,N]\)
边的权值 \(\leq 10^9\) 。
输入样例
6
3 1 1000
1 4 10
4 2 100
4 5 50
4 6 100
输出样例
1110
样例说明
直径共有两条,3 到2的路径和3到6的路径。这两条直径都经过边(3, 1)和边(1, 4)。
思路
模板题,树的直径。
考虑的是 \(f[u]\) 表示现在在 \(u\) 点的往下的最长的一条链。
现在考虑一下第二问怎么解答,虽然他并没有要求解答。有多少条直径,那么我现在先保存一个最大值,然后判断这个最大值被更新过多少次就ok了。
上die码:
#include <bits/stdc++.h>
using namespace std;
template <typename T>inline void read(T& t){
t=0; register char ch=getchar();
while(!('0'<=ch&&ch<='9')){if(ch=='-') t=-1;ch=getchar();}
while(('0'<=ch&&ch<='9')){t=((t<<1)+(t<<3))+ch-'0'; ch=getchar();}
}
template <typename T,typename... Args> inline void read(T& t, Args&... args){
read(t);read(args...);
}
template <typename T>inline void write(T x){
if(x<0) putchar('-'),x=~(x-1); int s[40],top=0;
while(x) s[++top]=x%10,x/=10; if(!top) s[++top]=0;
while(top) putchar(s[top--]+'0');
}
long long dis[314514],n,m;
char ch;
vector<pair<int,int> >a[314514];
long long ans;
void dfs(int u,int fa){
for(int i=0;i<a[u].size();++i){
int v=a[u][i].first;
if(v==fa) continue;
dfs(v,u);
ans=max(ans,a[u][i].second+dis[v]+dis[u]);
dis[u]=max(dis[v]+a[u][i].second,dis[u]);
}
}
int main(){
cin>>n;
for(int i=1;i<n;++i){
int x,y,w;
read(x,y,w);
a[x].push_back(make_pair(y,w));
a[y].push_back(make_pair(x,w));
}
dfs(1,-1);
cout<<ans<<endl;
return 0;
}
电脑网络
题目描述
一所学校在几年前购进了第一台电脑(这台电脑的编号为1)。最近几年,学校又购买了 \(N-1\) 台电脑,每台新电脑和之前的某一台电脑连接。学校的管理员想知道对于每一台电脑i,到与它距离最远的电脑的距离 \(S_i\) 。你需要提供这个信息。
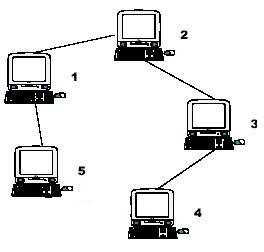
Hint: 样例输入如上图所示,从图中你可以知道,4号电脑到1号电脑的距离最远,所以 \(S_1=3\) 。4 号电脑和 5 号电脑到 2 号电脑的距离最远,所以 \(S_2=2\) 。 5 号电脑到 3 号电脑距离最远,所以\(S_3=3\)。由此类推 \(S_4=4\),\(S_5=4\)。
输入格式
第一行包含一个整数 \(N\) (\(N\leq 10000\)) ;
接下来 \(N-1\) 行描述每一台电脑。第 \(i\) 行包含两个用空格隔开的整数 \(y,l\) ,表示 \(i\) 号电脑与之前的 \(y\)号电脑连接,距离为l。
所有 \(l\) 之和不超过 \(10^9\) 。
输出格式
对于每组测试数据输出 \(N\) 行,第 \(i\) 行表示离 \(i\) 号电脑的最远距离 \(S_i\) 。
样例输入
5
1 1
2 1
3 1
1 1
样例输出
3
2
3
4
4
思路
这道题目运用了我认为一个巧妙的结论,在讲树的直径的时候也讲过了。
原来求树的直径,从一个点到他最远的点,然后再从那个最远的点到相对于它来说最远的点。
这说明什么,一个点到它最远的点肯定在树的直径的端点上。
那么就好办了,直接用三次 dfs ,第一次找到一个端点,第二次找到两个端点顺便记录一下从第一个找到端点到所有点的距离,第三次记录第二个找到的端点到所有点的距离,最后在两个距离里面取一个最大值就ok了。
蒟蒻die码:
#include <bits/stdc++.h>
#define pb push_back
using namespace std;
template <typename T>inline void read(T& t){
t=0; register char ch=getchar();
while(!('0'<=ch&&ch<='9')){if(ch=='-') t=-1;ch=getchar();}
while(('0'<=ch&&ch<='9')){t=((t<<1)+(t<<3))+ch-'0'; ch=getchar();}
}
template <typename T,typename... Args> inline void read(T& t, Args&... args){
read(t);read(args...);
}
template <typename T>inline void write(T x){
if(x<0) putchar('-'),x=~(x-1); int s[40],top=0;
while(x) s[++top]=x%10,x/=10; if(!top) s[++top]=0;
while(top) putchar(s[top--]+'0');
}
int n;
int dis[114514];
int dis1[114514];
vector<pair<int,int> >a[114514];
void dfs(int u,int fa){
for(int i=0;i<a[u].size();++i){
int v=a[u][i].first;
if(v==fa) continue;
dis[v]=dis[u]+a[u][i].second;
dfs(v,u);
}
}
void dfs1(int u,int fa){
for(int i=0;i<a[u].size();++i){
int v=a[u][i].first;
if(v==fa) continue;
dis1[v]=dis1[u]+a[u][i].second;
dfs1(v,u);
}
}
int main(){
cin>>n;
for(int i=2;i<=n;++i){
int x,y;
read(x,y);
a[i].push_back(make_pair(x,y));
a[x].push_back(make_pair(i,y));
}
dfs(1,-1);
int maxn=0,maxnum=0;
for(int i=1;i<=n;++i)
if(dis[i]>maxn){
maxn=dis[i];
maxnum=i;
}
dfs1(maxnum,-1);
maxn=0,maxnum=0;
for(int i=1;i<=n;++i)
if(dis1[i]>maxn){
maxn=dis1[i];
maxnum=i;
}
memset(dis,0,sizeof(dis));
dfs(maxnum,-1);
for(int i=1;i<=n;++i)
cout<<max(dis[i],dis1[i])<<endl;
return 0;
}
医院设置
题目描述
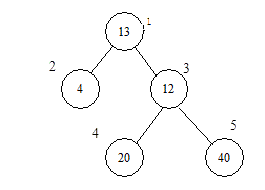
设有一棵二叉树(如图,其中圈中的数字表示结点中居民的人口,圈边上数字表示结点编号。现在要求在某个结点上建立一个医院,使所有居民所走的路程之和为最小,同时约定,相邻结点之间的距离为 1。就本图而言,若医院建在 1 处,则距离和 =4+12+220+240=136;若医院建在 3 处,则距离和 = 4*2+13+20+40=81…
输入格式
第一行一个整数 \(n\) ,表示树的结点数( \(n\leq 100\) )。 接下来的 \(n\) 行每行描述了一个结点的状况,包含三个整数,整数之间用空格(一个或多个)分隔,其中:第一个数为居民人口数;第二个数为左链接,为 0 表示无链接;第三个数为右链接,为 0 表示无链接。
输出格式
一个整数,表示最小距离和。
输入样例
5
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0
输出样例
81
思路
这道题数据量不是很大,才100,我现在用Floyd算法直接算答案都可以过,但是如果我这个数据在 \(1 \times 10^6\) ,那么就必须用我这种 \(O(n)\) 的办法了
首先思考,如果我现在已经确定了医院的位置并且算好了结果。
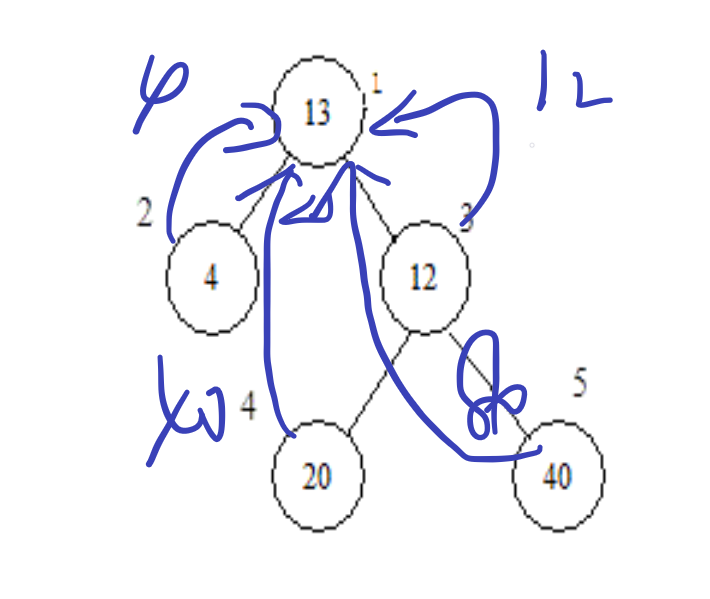
首先看这个图,表示了如果我现在医院就建在一号节点的情况,这样处理是 \(O(n)\) 的算法。
然后,我现在医院变更了,
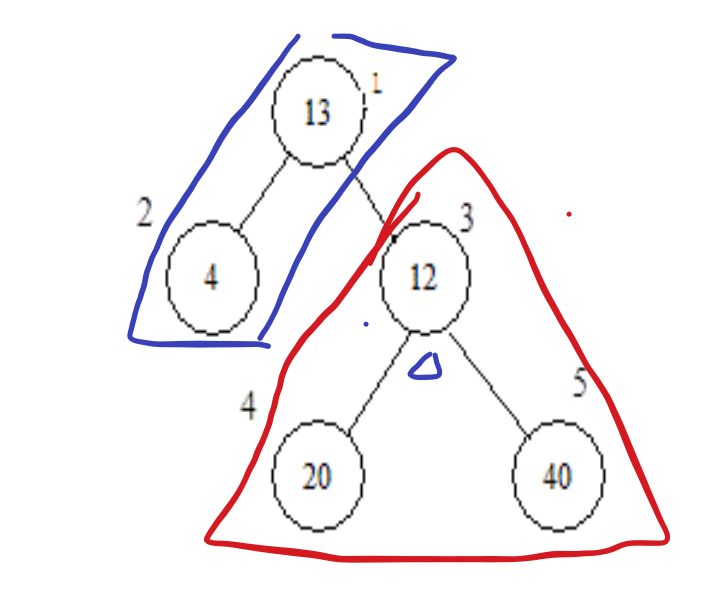
就像这个图,我现在医院变更了,可以看到,蓝色区域的节点都少走了已一步路,而其他节点都多走了一步路。
这叫做换根操作。请出换根的终极公式:
ok了,下面就上die码:
#include <bits/stdc++.h>
#define pb push_back
using namespace std;
template <typename T>inline void read(T& t){
t=0; register char ch=getchar();
while(!('0'<=ch&&ch<='9')){if(ch=='-') t=-1;ch=getchar();}
while(('0'<=ch&&ch<='9')){t=((t<<1)+(t<<3))+ch-'0'; ch=getchar();}
}
template <typename T,typename... Args> inline void read(T& t, Args&... args){
read(t);read(args...);
}
template <typename T>inline void write(T x){
if(x<0) putchar('-'),x=~(x-1); int s[40],top=0;
while(x) s[++top]=x%10,x/=10; if(!top) s[++top]=0;
while(top) putchar(s[top--]+'0');
}
int n;
struct Node{
int p,lc,rc;
}a[114514];
int f[114514],s[114514];
void dfs(int u,int s){
f[1]+=s*a[u].p;
if(a[u].lc) dfs(a[u].lc,s+1);
if(a[u].rc) dfs(a[u].rc,s+1);
return;
}
void dfss(int u,int fa){
s[u]=a[u].p;
if(a[u].lc){
dfss(a[u].lc,u);
s[u]+=s[a[u].lc];
}
if(a[u].rc){
dfss(a[u].rc,u);
s[u]+=s[a[u].rc];
}
return;
}
void ddfs(int u,int fa){
if(a[u].lc){
f[a[u].lc]=f[u]-2*s[a[u].lc]+s[1];
ddfs(a[u].lc,u);
}
if(a[u].rc){
f[a[u].rc]=f[u]-2*s[a[u].rc]+s[1];
ddfs(a[u].rc,u);
}
}
int main(){
cin>>n;
for(int i=1;i<=n;++i) read(a[i].p,a[i].lc,a[i].rc);
dfs(1,0);
dfss(1,-1);
ddfs(1,-1);
int ans=0x3f3f3f3f;
for(int i=1;i<=n;++i)
ans=min(ans,f[i]);
cout<<ans<<endl;
return 0;
}
「NOIP2018 提高组」赛道修建
题目描述
C 城将要举办一系列的赛车比赛。在比赛前,需要在城内修建 \(m\) 条赛道。
C 城一共有 \(n\) 个路口,这些路口编号为 \(1,2,…,n\) ,有 \(n−1\) 条适合于修建赛道的双向通行的道路,每条道路连接着两个路口。其中,第 \(i\) 条道路连接的两个路口编号为 \(a_i\) 和 \(b_i\) ,该道路的长度为 \(l_i\) 。借助这 \(n−1\) 条道路,从任何一个路口出发都能到达其他所有的路口。
一条赛道是一组互不相同的道路 \(e_1,e_2,…,e_k\),满足可以从某个路口出发,依次经过 道路 \(e_1,e_2,…,e_k\) (每条道路经过一次,不允许调头)到达另一个路口。一条赛道的长度等于经过的各道路的长度之和。为保证安全,要求每条道路至多被一条赛道经过。
目前赛道修建的方案尚未确定。你的任务是设计一种赛道修建的方案,使得修建的 \(m\) 条赛道中长度最小的赛道长度最大(即 \(m\) 条赛道中最短赛道的长度尽可能大)
输入格式
第一行包含两个由空格分隔的正整数 \(n,m\),分别表示路口数及需要修建的 赛道数。
接下来 \(n−1\) 行,第 i 行包含三个正整数 \(a_i,b_i,l_i\) ,表示第 \(i\) 条适合于修建赛道的道 路连接的两个路口编号及道路长度。保证任意两个路口均可通过这 \(n−1\) 条道路相互到达。每行中相邻两数之间均由一个空格分隔。
输出格式
输出共一行,包含一个整数,表示长度最小的赛道长度的最大值。
数据范围与提示

其中,“分支不超过 3”的含义为:每个路口至多有 3 条道路与其相连。
对于所有的数据, \(2≤n≤50,000, 1≤m≤n−1, 1≤ai,bi≤n, 1≤li≤10,000。\)
输入样例
7 1
1 2 10
1 3 5
2 4 9
2 5 8
3 6 6
3 7 7
输出样例
31
思路
说实话,这题太适合我了,是二分+树上dp的好题。
如果这题能是2021csp-s最后一题我直接起飞
不多说,首先看到要求的答案竟然是最小赛道长度的最大值,直接二分答案。将答案变为了判断性问题。
我的 left 和 right 都是闭区间,是从 left 到 right 都可以成功,我认为这样理解更为简单。
可以先去看那个只有3个分支的,那个是正解的弱化数据。
对于三个分支,我现在就只可能有父亲节点,双儿子节点,对于每一条路径,对答案的贡献最多是1,然后我只需要查看一下两个节点的最长链加起来是不是大于了我现在要判断的答案。
题目还是很水的。
#include <bits/stdc++.h>
#define pb push_back
using namespace std;
template <typename T>inline void read(T& t){
t=0; register char ch=getchar();
while(!('0'<=ch&&ch<='9')){if(ch=='-') t=-1;ch=getchar();}
while(('0'<=ch&&ch<='9')){t=((t<<1)+(t<<3))+ch-'0'; ch=getchar();}
}
template <typename T,typename... Args> inline void read(T& t, Args&... args){
read(t);read(args...);
}
template <typename T>inline void write(T x){
if(x<0) putchar('-'),x=~(x-1); int s[40],top=0;
while(x) s[++top]=x%10,x/=10; if(!top) s[++top]=0;
while(top) putchar(s[top--]+'0');
}
int n,m;
struct Edge{
int to,nxt,w;
}e[114514];
vector<pair<int,int> >a[114514];
int s,cnt,pos;
int h[114514];
int f[114514];
void add(int u,int v,int w){
e[++pos].to=v;
e[pos].w=w;
e[pos].nxt=h[u];
h[u]=pos;
}
void dfs(int u,int fa,int pos){
multiset<int>se;
for(int i=h[u];i;i=e[i].nxt){
int v=e[i].to,w=e[i].w;
if(v==fa) continue;
dfs(v,u,pos);
if(f[v]+w>=pos){
cnt++;
continue;
}
se.insert(f[v]+w);
}
while(!se.empty()){
multiset<int>::iterator q=se.begin();
se.erase(q);
multiset<int>::iterator p=se.lower_bound(pos-*q);
if(p!=se.end()){
cnt++;
se.erase(p);
}else f[u]=max(f[u],*q);
}
}
bool check(int x){
memset(f,0,sizeof(f));
cnt=0;
dfs(1,-1,x);
if(cnt>=m) return 1;
else return 0;
}
int main(){
cin>>n>>m;
for(int i=1;i<n;++i){
int x,y,w;
read(x,y,w);
s+=w;
add(x,y,w);
add(y,x,w);
}
int left=1,right=s/m+1;
//left到right都可以
while(left<right){
int mid=(left+right+1)>>1;
if(check(mid)) left=mid;
else right=mid-1;
}
cout<<left<<endl;
return 0;
}
//19+12 31
这里可以不用领接表,但是我害怕还是水了一个。
完结撒花!


