如何玩转ST表

对于ST表，它是一个大毒瘤比较好用的数据结构，他支持 \(O(1)\) 查询，而预处理是 \(O(n\log n)\) 的。

对于ST表，在我认为看起来像是一种dp思想。他记录了当前的答案，并把当前的答案传导下去。

而对于每个状态，我们用 \(st[i][j]\) 表示从 \(i\) 开始的连续 \(2^j\) 个元素中的最大/小值。

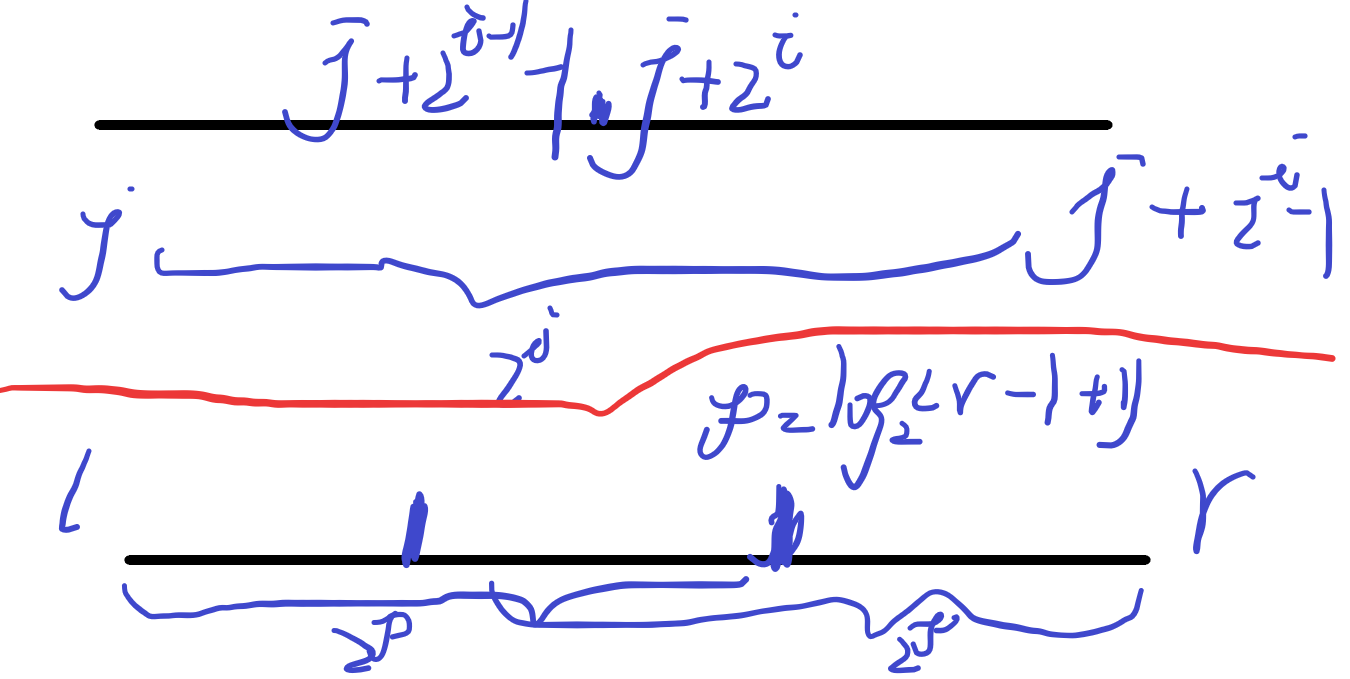
如何初始化呢？上面一幅图的上半部分其实是比较清晰的。 对于每一个 \(st[i][j]\) 它就等于 \(\max(st[i][j-1],st[i+(1<<j-1)][j-1])\) 由图可知，这样的话一个 \(2^j\) 次方的区间被分成了两个 \(2^(j-1)\) 次方的区间，这就是二分的思想，也是一种倍增的思想。所以这个的时间复杂度是 \(O(n\times \log n)\) 的。

非常好用！

如何查询呢，查询是上面一幅图的下半部分。这里遇到的小问题就是，我所给出的 \((l,r)\) 的区间，这个区间的长度不一定为 \(2^k\) ，那该如何查询呢，其实思路还是将它分成两个 \(2^(k-1)\) 的区间，这个让这两个区间正好可以覆盖这个区间，即使中间有重复。

不难想到，这个 \(k = \log (r-l+1)\) ，然后就只需要像图上那样，查询就可以做到 \(O(1)\) 啦。

你谷ST表模板。P3685

#include <bits/stdc++.h>
#define debug puts("I ak IOI several times");
#define pb push_back
using namespace std;
template <typename T>inline void read(T& t){
    t=0; register char ch=getchar();
    while(!('0'<=ch&&ch<='9')){if(ch=='-') t=-1;ch=getchar();}
    while(('0'<=ch&&ch<='9')){t=((t<<1)+(t<<3))+ch-'0'; ch=getchar();}
}
template <typename T,typename... Args> inline void read(T& t, Args&... args){
    read(t);read(args...);
}
template <typename T>inline void write(T x){
    if(x<0) putchar('-'),x=~(x-1); int s[40],top=0;
    while(x) s[++top]=x%10,x/=10; if(!top) s[++top]=0;
    while(top) putchar(s[top--]+'0');
}
int n,m;
int f[100005][27];
int a[100005];
void intt(){
    read(n,m);
    for(int i=1;i<=n;++i) read(a[i]);
    for(int i=1;i<=n;++i) f[i][0]=a[i];
    for(int k=1;k<=22;++k)
        for(int i=1;i+(1<<k)-1<=n;++i)
            f[i][k]=max(f[i][k-1],f[i+(1<<k-1)][k-1]);
    return;
}
int solve(int l,int r){
    int logk=log2(r-l+1);
    return max(f[l][logk],f[r-(1<<logk)+1][logk]);
}
int main(){
    intt();
    while(m--){
        int l,r;
        read(l,r);
        write(solve(l,r));
        putchar('\n');
    }
    return 0;
}
//Welcome back,Chtholly.